Из последнего равенства аналогичным образом для некоторого целого неотрицательно-
го s 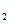 получаем
получаем
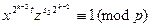 ,
, 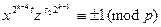 .
.
Повторяя эту процедуру еще k-3 раза, получим для некоторого неотрицательного s 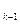
равенство
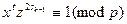 .
.
Из него, наконец, находим
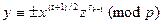 .
.
4. Задача распознавания квадратичного вычета по модулю 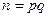 .
.
Формулировка задачи в этом случае выглядит так:
Задано: 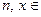 N,
N, 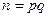 , p и q – различные простые нечетные,
, p и q – различные простые нечетные, 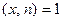 .
.
Распознать: существует ли такое у 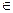 Z, что
Z, что 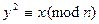 ?
?
Решение этой задачи сводится к факторизации числа 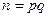 .
.
5. Задача извлечения квадратного корня по модулю 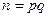 .
.
Формулировка задачи выглядит так:
Задано: 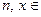 N,
N, 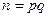 , p и q – различные простые нечетные,
, p и q – различные простые нечетные, 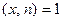 .
.
Найти: такое у 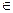 Z, что
Z, что 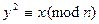 , если у существует.
, если у существует.
Ответ на вопрос этой задачи (как и обоснование ответа к предыдущей) дает теорема:
Теорема. Пусть 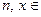 N,
N, 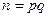 , p и q – различные простые нечетные,
, p и q – различные простые нечетные, 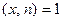 . Обозначим
. Обозначим 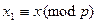 и
и 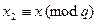 . Тогда
. Тогда
1) Если существует такое у 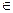 Z, что
Z, что
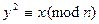 , (7.1) то для
, (7.1) то для 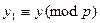 и
и 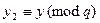 (7.2) выполняется
(7.2) выполняется 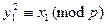 и
и 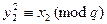 . (7.3) Справедливо и обратное: для любых
. (7.3) Справедливо и обратное: для любых 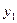 и
и 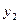 из (7.3) у из (7.2) удовлетворяет (7.1).
из (7.3) у из (7.2) удовлетворяет (7.1).
2) х является квадратичным вычетом по модулю n тогда и только тогда, когда х есть квадратичный вычет по модулю р и по модулю q.
3) Если х – квадратичный вычет по модулю n, то существует ровно четыре различных корня квадратных из х по модулю n.
В последнем пункте следует поступать так. Комбинируя пары решений по mod p и mod q, следует решать далее системы сравнений вида
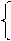 u = x
u = x 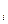 (mod p),
(mod p),
u = x 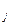 (mod q), где i,j = 1,2.
(mod q), где i,j = 1,2.
Решения этих систем дают искомые четыре варианта корня квадратного из x по mod n.
Итак, как видно из теоремы, и задача нахождения квадратного корня по модулю n сводится полиномиально к задаче факторизации. Оказывается, что существует и обратное сведение, т.е. задачу факторизации числа 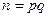 можно свести к задаче извлечения квадратного корня по модулю n.
можно свести к задаче извлечения квадратного корня по модулю n.
Теорема. Пусть 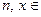 N,
N, 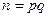 , p и q – различные простые нечетные,
, p и q – различные простые нечетные, 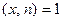 , а
, а 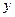 и
и 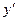 – два различных корня из х по модулю n таких, что
– два различных корня из х по модулю n таких, что 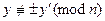 . Тогда
. Тогда 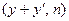 есть один из делителей р или q.
есть один из делителей р или q.
Легко представить простой Лас-Вегас оракульный алгоритм, который факторизует числа n указанного вида с доступом к оракулу 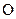 , который поставляет корень квадратный
, который поставляет корень квадратный 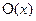 по запросу х.
по запросу х.
Вход: n = pq, где p и q – различные простые нечетные.
1. Выбрать случайный элемент 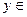 Z
Z 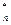 .Вычислить
.Вычислить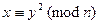 .
.
2. Сделать оракулу 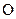 запрос x. Пусть
запрос x. Пусть 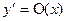 – ответ оракула, т.е.
– ответ оракула, т.е. 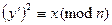 .
.
3. Если выполняется условие 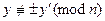 , то вычислить с помощью алгоритма
, то вычислить с помощью алгоритма
Евклида 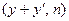 и результат падать на выход.
и результат падать на выход.
Так как y выбирается случайно, то согласно пункту 3 предыдущей теоремы условие 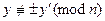 выполняется с вероятностью ½. Если применить алгоритм k раз, то вероятность того, что это условие не выполнится ни разу, составит
выполняется с вероятностью ½. Если применить алгоритм k раз, то вероятность того, что это условие не выполнится ни разу, составит  .
.
Раздел восьмой
1. Вычисление значений функции Эйлера 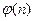 .
.
Как известно, функция Эйлера мультипликативна, поэтому по каноническому разложению числа n легко получить значение 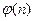 . Если же каноническое разложение числа неизвестно, то задача становится сложной. В настоящее время неизвестны эффективные алгоритмы решения задачи:
. Если же каноническое разложение числа неизвестно, то задача становится сложной. В настоящее время неизвестны эффективные алгоритмы решения задачи:
Задано: n 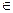 N.
N.
Найти: 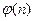 .
.
Для криптографических приложений нас интересует задача вычисления значения 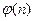 в случае, когда
в случае, когда 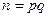 . Легко видеть, что
. Легко видеть, что 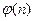 = (р-1) (q-1). Таким образом, если р и q известны, то задача решается просто. С другой стороны, если известны n и
= (р-1) (q-1). Таким образом, если р и q известны, то задача решается просто. С другой стороны, если известны n и 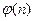 , то решая уравнение
, то решая уравнение 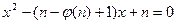 , получаем p и q. Значит, задача сводится к суженной задаче факторизации. Справедливо и обратное сведение. Таким образом, эти две задачи полиномиально эквивалентны.
, получаем p и q. Значит, задача сводится к суженной задаче факторизации. Справедливо и обратное сведение. Таким образом, эти две задачи полиномиально эквивалентны.
2. Задачи распознавания и построения первообразных корней по модулю р.
Первая из задач формулируется так.
Задано: р – простое нечетное, 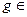 N.
N.
Распознать: порождает ли g группу Z 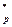 ?
?
Для этой задачи неизвестны ни детерминированные, ни вероятностные полиномиальные алгоритмы. Но если задано каноническое разложение числа р – 1, то задача решается простой проверкой условий:
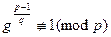 для любого простого
для любого простого 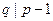 .
.
Таким образом, видно, что указанная задача полиномиально сводится к задаче факторизации числа р – 1 (возведение в степень осуществляется бинарным методом)
Вторая задача формулируется следующим образом.
Задано: простое нечетное р.
Найти: 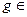 Nтакое,что g порождает группу Z
Nтакое,что g порождает группу Z 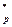 .
.
И для этой задачи неизвестны эффективные алгоритмы. Можно лишь указать очевидное вероятностное сведение второй задачи к первой. Учитывая, что существует 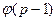 первообразных корней по модулю р, вероятность неудачи равна
первообразных корней по модулю р, вероятность неудачи равна 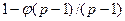 . Это сведение можно использовать для такой ослабленной задачи нахождения первообразного корня:
. Это сведение можно использовать для такой ослабленной задачи нахождения первообразного корня:
Задано: простое нечетное р, 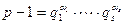 .
.
Найти: 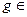 Nтакое,что g порождает группу Z
Nтакое,что g порождает группу Z 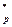 .
.
Сформулируем еще один вариант решения задачи построения первообразного корня по простому модулю.
Задано: n 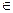 N.
N.
Найти: р и 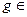 Nтакие,что р – простое,
Nтакие,что р – простое, 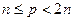 , а g порождает группу Z
, а g порождает группу Z 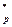 .
.
Для решения этой задачи применяется полиномиальная вероятностная процедура порождения случайного числа х из промежутка от n до 2n вместе с его разложением на простые множители. Далее производится тестирование числа х+1 на простоту. Если х+1 – число простое, то полагают р = х+1. Если тест не пройден, то выбирают другое х. Следовательно, при положительном решении такой задачи можно переходить к задаче построения первообразного корня по модулю р. Заметим, что в этом случае р есть случайное простое заданного размера.
2. Задача дискретного логарифмирования.
Рассмотрим задачу дискретного логарифмирования по простому модулю.
Задано: 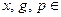 N, где р – простое нечетное,
N, где р – простое нечетное, 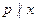 ; g – первообразный корень по
; g – первообразный корень по
модулю р.
Найти: у такое, что 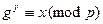 .
.
По состоянию на сегодняшний день эта задача является трудной. Время лучших алгоритмов имеет такую же асимптотику, как и в случае задачи факторизации, хотя связи между этими задачами не обнаружено.
3. Алгоритм «Шаг лилипута, шаг великана» дискретного логарифмирования.
Это один из первых алгоритмов (1973 г.), который показал, что задача вычисления дискретного логарифма может быть решена быстрее, чем методом перебора.
Вход: 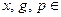 N, где р – простое нечетное,
N, где р – простое нечетное, 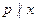 ; g – первообразный корень по
; g – первообразный корень по
модулю р.
1. Выбрать два натуральных числа m и k такие, что 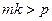 . (8.1)
. (8.1)
2. Вычислить два ряда чисел

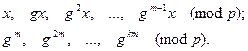 (8.2)
(8.2)
3. Найти такие i и j, для которых выполняется равенство
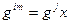 .
.
4. Число 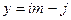 подать на выход.
подать на выход.
Покажем корректность алгоритма. Действительно,
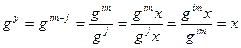 .
.
Остается проверить, что указанные i и j существуют. Легко видеть, что разности 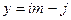 пробегают промежуток целых чисел от1 до
пробегают промежуток целых чисел от1 до 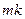 , т.е. > p вариантов. Если бы
, т.е. > p вариантов. Если бы
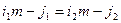 ,
,
то тогда
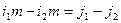 ,
,
откуда
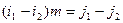
и, значит,
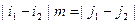 ,
,
но
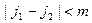 .
.
Поэтому найдется показатель 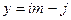 по
по 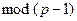 , который удовлетворяет условию
, который удовлетворяет условию 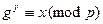 .
.
Оценим сложность этого метода.
Теорема. Время работы алгоритма «Шаг лилипута, шаг великана» для достаточно больших p удовлетворяет неравенству
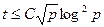 . (8.3)
. (8.3)
Доказательство. Выберем
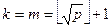 ,
,
так что (8.1) выполняется. Тогда в (8.2) потребуется не более 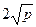 операций умножения. Известно, что для выполнения операций умножения и деления с остатком требуется
операций умножения. Известно, что для выполнения операций умножения и деления с остатком требуется 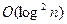 элементарных операций, где
элементарных операций, где 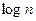 есть длина операндов. Таким образом, получено время вычисления рядов (8.2). Но кроме этого требуется еще найти среди полученных чисел равные. Сначала перенумеруем числа в рядах (8.2) с добавлением одного бита принадлежности к данному ряду, преобразуем обе последовательности в список и отсортируем по величине. Длина общего ряда равна
есть длина операндов. Таким образом, получено время вычисления рядов (8.2). Но кроме этого требуется еще найти среди полученных чисел равные. Сначала перенумеруем числа в рядах (8.2) с добавлением одного бита принадлежности к данному ряду, преобразуем обе последовательности в список и отсортируем по величине. Длина общего ряда равна 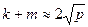 . Для лучших алгоритмов сортировки требуется
. Для лучших алгоритмов сортировки требуется 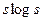 операций сравнения, где s – длина списка. В нашем случае потребуется
операций сравнения, где s – длина списка. В нашем случае потребуется 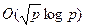 операций сравнения над словами длины
операций сравнения над словами длины 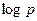 бит. Таким образом, требуется
бит. Таким образом, требуется 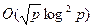 операций. После сортировки объединенного ряда его надо просмотреть и найти два равных числа из разных рядов (8.2), используя битовый признак. В итоге получается оценка (8.3).
операций. После сортировки объединенного ряда его надо просмотреть и найти два равных числа из разных рядов (8.2), используя битовый признак. В итоге получается оценка (8.3).
4. Алгоритм Силвера-Полига-Хеллмана дискретного логарифмирования.
Этот алгоритм предполагает, что число р –1 имеет «небольшие» простые делители, точнее любое простое 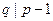 ограничено некоторым общим для всех числом r, что позволяет произвести факторизацию р – 1. Его время работы ограничено полиномом от
ограничено некоторым общим для всех числом r, что позволяет произвести факторизацию р – 1. Его время работы ограничено полиномом от 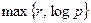 . Пусть
. Пусть 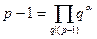 – каноническое разложение числа р – 1. Для каждого
– каноническое разложение числа р – 1. Для каждого 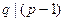 найдем
найдем 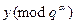 , после чего по Китайской теореме найдем искомое у. Представим
, после чего по Китайской теореме найдем искомое у. Представим
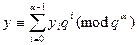 , где
, где 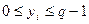 .
.
Требуется найти последовательность 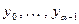 . Заметим, что
. Заметим, что
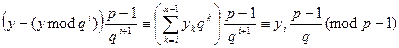
для  . Отсюда имеем
. Отсюда имеем
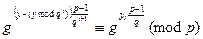 ,
,
что можно переписать в виде
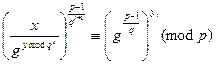 . (8.1)
. (8.1)
Покажем, как из последнего сравнения получить 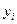 . При
. При 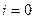 получаем условие
получаем условие
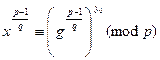 . (8.2)
. (8.2)
С помощью бинарного метода возведения в степень вычислим последовательность чисел
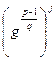 для
для 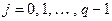 . (8.3)
. (8.3)
Заметим, что все элементы последовательности попарно различны, ибо g – первообразный корень. Вычислим также степень 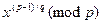 , которая по (8.2) должна совпасть с одним из членов последовательности (8.3). Тогда коэффициент
, которая по (8.2) должна совпасть с одним из членов последовательности (8.3). Тогда коэффициент 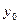
равен соответствующему показателю j.
Допустим, что уже найдены 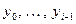 . Тогда можно вычислить левую часть сравнения (8.1) по модулю р, так как
. Тогда можно вычислить левую часть сравнения (8.1) по модулю р, так как 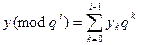 . Сравнивая результат с членами последовательности (8.3), находим
. Сравнивая результат с членами последовательности (8.3), находим 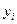 . Это завершает описание алгоритма.
. Это завершает описание алгоритма.
Лучший на сегодняшний день (2005 г.) алгоритм имеет время работы
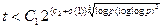 , где
, где 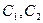 > 0 – константы.
> 0 – константы.
Раздел девятый
1. Концепция криптосистем с открытым ключом.
В 1976 г. американцы W. Diffy и M. Hellmann предложили новую концепцию т. н. двухключевой криптографии, в которой процедура шифрования является общедоступной, а расшифрование может успешно провести лишь тот, кто владеет секретным ключом. Таким образом, система требует наличия двух ключей – открытого, находящегося в общем пользовании, и закрытого, секретного, которым владеет лишь адресат. Это добавляет к общей схеме закрытого информационного обмена специальный генератор ключей, который вырабатывает соответствующие пары.
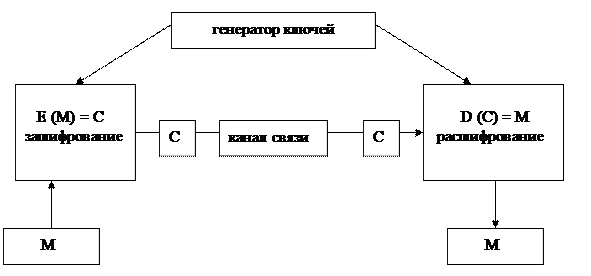
В симметричных системах ключ зашифрования и расшифрования мог быть один или, если их два, каждый из них получался из другого полиномиальной процедурой. Значит, оба ключа надо держать в секрете. В двухключевой криптографии секретный ключ получить из открытого легко не представляется возможным в силу большой вычислительной сложности соответствующей задачи. Такие системы стали называть асимметричными, или системами с открытым ключом.
2. Формальные составляющие асимметричных криптосистем.
Необходимыми составляющими любой асимметричной криптосистемы являются следующие:
1) алфавиты открытых и закрытых текстов;
2) пространство ключей (множество слов в некотором алфавите);
3) алгоритм генерирование ключей – вероятностный полиномиальный алгоритм, который получив на вход 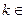 N,где k – параметр безопасности, дает на выходе случайную пару
N,где k – параметр безопасности, дает на выходе случайную пару 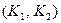 , принадлежащую ключевому пространству, и где
, принадлежащую ключевому пространству, и где 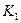 называется открытым ключом и применяется для зашифрования, а
называется открытым ключом и применяется для зашифрования, а 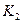 – секретным и применяется для расшифрования;
– секретным и применяется для расшифрования;
4) полиномиальный детерминированный алгоритм зашифрования Е, который получив на вход открытое сообщение М и открытый ключ 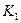 , дает на выходе шифртекст С, что записывается в виде
, дает на выходе шифртекст С, что записывается в виде 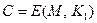 ;
;
5) полиномиальный детерминированный алгоритм расшифрования D, который получив на вход шифртекст С и секретный ключ 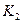 , дает на выход открытый текст М, что записывается в виде
, дает на выход открытый текст М, что записывается в виде 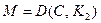 .
.
Перечисленные алгоритмы должны удовлетворять следующим условиям:
1) если пара 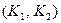 получена генератором производства ключей, то для любого открытого текста М должно из
получена генератором производства ключей, то для любого открытого текста М должно из 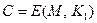 следовать
следовать 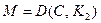 ;
;
2) неизвестны (или не существуют) эффективные алгоритмы, которые позволяют по известным 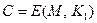 и
и 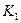 находить М.
находить М.
Первое условие гарантирует восстановление любого открытого текста из зашифрованного, а второе обеспечивает надежность системы. Из второго условия, в частности, следует, что неизвестен эффективный алгоритм, который бы по известному открытому ключу 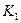 производил пару
производил пару 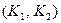 , которая, в свою очередь, могла быть порожденной алгоритмом генерирования ключей.
, которая, в свою очередь, могла быть порожденной алгоритмом генерирования ключей.
3. Криптосистема RSA.
Криптосистема RSA предложена в 1977 г. Ее авторами являются R. Rivest, A. Shamir, L. Adleman. Это одна из самых известных асимметричных систем.
1) Генерирование ключей.
Выбираются два больших различных простых числа р и q, вычисляется их произведение 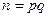 и значение функции Эйлера
и значение функции Эйлера 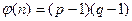 . Затем выбирается случайное число
. Затем выбирается случайное число 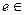 Z
Z 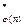 и вычисляется d такое, что
и вычисляется d такое, что 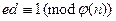 . После этого полагают открытым ключом числа n и e, а секретным ключом – число d.
. После этого полагают открытым ключом числа n и e, а секретным ключом – число d.
2) Зашифрование.
RSA – система блочная. Открытый текст разбивается на блоки, каждый из которых рассматривается как элемент кольца Z 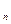 . Таким образом, для двоичной записи блока длины m должно выполняться неравенство
. Таким образом, для двоичной записи блока длины m должно выполняться неравенство 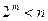 . Если М есть блок открытого текста, то результат его шифрования выглядит так:
. Если М есть блок открытого текста, то результат его шифрования выглядит так:
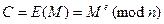 .
.
3) Расшифрование.
Процедура расшифрования выглядит также просто:
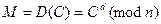 .
.
Укажем на корректность процедуры, т.е. что действительно для любого открытого текста М выполняется условие M = D(E(M)). Пусть 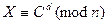 . Это сравнение можно свести к системе сравнений
. Это сравнение можно свести к системе сравнений
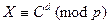 ,
,
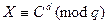 .
.
Рассмотрим первое из них, привлекая теорему Ферма.
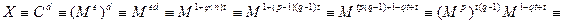
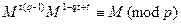 .
.
То же проделаем и со вторым сравнением. В итоге получим требуемое, так как р и q числа взаимно простые.
Для каждого из описанных действий существуют эффективные алгоритмы. Именно: для построения больших простых чисел, выбора числа е и решения сравнения по большому модулю (расширенный алгоритм Евклида), для процедур зашифрования и расшифрования (бинарный метод). Это говорит в пользу эффективности системы в целом.
Наконец, следует сказать о стойкости криптосистемы. Любую систему можно считать стойкой, если задача нахождения открытого текста по шифртексту и открытому ключу является сложной. В данном случае эта задача выглядит так.
Задано: 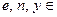 N , где
N , где 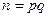 и
и 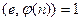 .
.
Найти: х такое, что 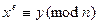 .
.
Таким образом, задача слома системы сводится к задаче извлечения корня е-й степени по модулю 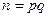 . На сегодняшний день для такой задачи неизвестны эффективные алгоритмы. Но и не доказано, что таких алгоритмов не существует. С другой стороны, любую асимметричную систему можно сломать, если указать эффективный алгоритм получения секретного ключа из открытого. Поэтому сформулируем еще одну задачу.
. На сегодняшний день для такой задачи неизвестны эффективные алгоритмы. Но и не доказано, что таких алгоритмов не существует. С другой стороны, любую асимметричную систему можно сломать, если указать эффективный алгоритм получения секретного ключа из открытого. Поэтому сформулируем еще одну задачу.
Задано: 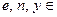 N , где
N , где 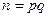 и
и 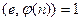 .
.
Найти: d такое, что 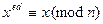 для всех х.
для всех х.
Из алгоритма генерирования ключей вытекает, что решение такой задачи сводится к вычислению значения функции Эйлера 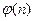 , что на сегодня является трудной задачей, если неизвестны множители р и q. Для того, чтобы лишить противников всякой надежды на возможность факторизации числа n, р и q выбирают величиной порядка
, что на сегодня является трудной задачей, если неизвестны множители р и q. Для того, чтобы лишить противников всякой надежды на возможность факторизации числа n, р и q выбирают величиной порядка 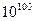 , так что число n имеет порядок
, так что число n имеет порядок 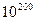 . Итак, задачу нахождения секретного ключа можно свести к факторизации числа n, а последняя является сложной. Все это говорит в пользу того факта, что криптосистему в настоящее время считают стойкой при надлежащем выборе параметров безопасности. Числа р и q выбирают сильными простыми (см. з.7). Добавим к сказанному, что при том, что р и q должны быть большими, они не должны сильно отличаться друг от друга, но и не должны быть слишком близки друг другу. Наконец, р и q должны быть таковы, чтобы наибольший общий делитель чисел р-1 и q-1 был небольшим, желательно, чтобы
. Итак, задачу нахождения секретного ключа можно свести к факторизации числа n, а последняя является сложной. Все это говорит в пользу того факта, что криптосистему в настоящее время считают стойкой при надлежащем выборе параметров безопасности. Числа р и q выбирают сильными простыми (см. з.7). Добавим к сказанному, что при том, что р и q должны быть большими, они не должны сильно отличаться друг от друга, но и не должны быть слишком близки друг другу. Наконец, р и q должны быть таковы, чтобы наибольший общий делитель чисел р-1 и q-1 был небольшим, желательно, чтобы 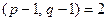 . Нарушение любого из этих условий позволяет применить к числу n один из эффективных алгоритмов факторизации. Имеются и некоторые другие секреты использования RSA.
. Нарушение любого из этих условий позволяет применить к числу n один из эффективных алгоритмов факторизации. Имеются и некоторые другие секреты использования RSA.
Рассмотрим небольшой пример. Выберем простые p и q. Пусть р = 997, q = 977. Тогда n = 974069, a 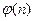 = (р – 1)(q – 1) = 972096. Положим е= 868121, и решая сравнение ed = 1 (mod
= (р – 1)(q – 1) = 972096. Положим е= 868121, и решая сравнение ed = 1 (mod 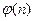 ), получаем, что d = 586025. Итак, сформированы ключи криптосистемы. Пусть задан открытый текст
), получаем, что d = 586025. Итак, сформированы ключи криптосистемы. Пусть задан открытый текст
«BETTER LATE THAN NEVER».
При длине алфавита равной 27 получаем следующий цифровой текст:
«01041919041726110019042619070013261304210417».
Разобьем его на блоки длины 4:
«0104 1919 0417 2611 0019 0426 1907 0013 2613 0421 0417».
Возводя каждый блок в степень е = 868121 по mod 974069, получаем цифровой криптотекст:
“491794 547096 837824 773497 682113 110037 449993 489740 770973 767593 837824”
Если теперь каждый блок этого текста возвести в степень d = 586025 по mod 974069, то
получим исходный цифровой текст.
Легко видеть, что в системе RSA не шифруются некоторые сообщения, например, 0 или 1. Справедлива
Теорема. В условиях RSA сравнение 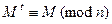 выполняется для всех
выполняется для всех 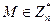
тогда и только тогда, когда 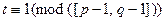 .
.
Доказательство. Действительно, из сравнения 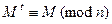 следует система
следует система
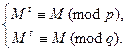
Рассмотрим первое из сравнений системы. Если 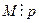 , то сравнение выполнимо. Поэтому пусть
, то сравнение выполнимо. Поэтому пусть 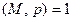 . Тогда сокращая обе части сравнения на М, получаем:
. Тогда сокращая обе части сравнения на М, получаем:
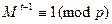 .
.
Но по теореме Ферма 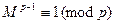 , и так как среди М встречаются первообразные корни по mod p, то
, и так как среди М встречаются первообразные корни по mod p, то 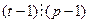 . Подобный вывод справедлив и для простого q, откуда и следует необходимость. С другой стороны, если
. Подобный вывод справедлив и для простого q, откуда и следует необходимость. С другой стороны, если 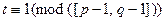 , то, например, сравнение
, то, например, сравнение
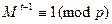
заведомо выполняется, а потому выполняется и первое сравнение системы. То же можно утверждать и для второго сравнения системы, а окончательный результат следует из Китайской теоремы.
Доказанное утверждение, в частности, говорит о том, что выбирая часть е открытого ключа, следует учитывать появляющуюся возможность «нешифрования» сообщения.
Рассмотрим одну из возможных атак на RSA – метод повторного шифрования. Итак,
пусть 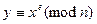 , при этом
, при этом 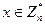 и, значит, также
и, значит, также 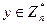 . Строим последовательность
. Строим последовательность 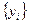 :
:
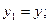
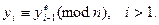
Это значит, что
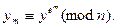
Поскольку 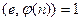 , то существует натуральное число m такое, что
, то существует натуральное число m такое, что 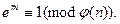 Но тогда
Но тогда
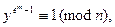
откуда вытекает
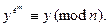
Тогда 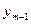 будет решением рассматриваемого сравнения.
будет решением рассматриваемого сравнения.
Сформулируем еще теорему М.Винера.
Теорема. Пусть задана RSA-криптосистема с параметрами
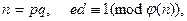
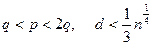 .
.
Тогда d эффективно вычислимо.
Существует предположение, что все секретные элементы 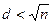 небезопасны.
небезопасны.
4. Криптосистема Рабина.
Система предложена в 1979 г. Rabin’ым.
1) Генерирование ключей.
Выбирают два больших различных простых числа р и q, вычисляют их произведение 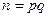 . Полагают открытым ключом число n, а секретным – р и q.
. Полагают открытым ключом число n, а секретным – р и q.
2) Зашифрование.
Шифрование производится поблочно в соответствии с формулой
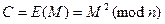 .
.
3) Расшифрование.
Процедура расшифрования предполагает для получения блока М извлечь корень квадратный из С. Зная р и q это можно осуществить эффективно. Так как имеется четыре корня по модулю n, то при переходе к буквенному тексту берут тот, что обладает смысловым содержанием. Несложная модификация алгоритма делает шифрующее отображение инъективным.
Замечание. При описании алгоритма исходили из допущения, что 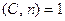 (это эквивалентно тому, что
(это эквивалентно тому, что 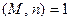 ). Пересылку таких сообщений следует исключить, ибо противник может получить нетривиальный делитель числа n.
). Пересылку таких сообщений следует исключить, ибо противник может получить нетривиальный делитель числа n.
Корректность процедуры очевидна. Если говорить об эффективности, то легко видеть, что легитимный пользователь системы обладает необходимым набором эффективных алгоритмов как при генерировании ключей, так и при действиях зашифрования и расшифрования.
Стойкость криптосистемы основывается на сложности задачи извлечения корня квадратного из числа С по модулю 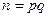 . Как уже говорилось, такая задача по сложности эквивалентна задаче факторизации (эта задача в данном случае совпадает с задачей нахождения секретного ключа по открытому).
. Как уже говорилось, такая задача по сложности эквивалентна задаче факторизации (эта задача в данном случае совпадает с задачей нахождения секретного ключа по открытому).
Рассмотрим пример. Пусть теперь р = 997, а q = 991. Тогда n = 988027. Предлагается зашифровать текст:
“ARGUMENTUM OMNI DENUDATUM ORNAMENTO”.
Запишем цифровой эквивалент этой фразы:
«001706201204131920122614121308260304132003001920122614171300120413191409»
Эту запись разобьем на блоки длины 6, для чего в конце дописана буква «J» с номе-
ром 09. Имеем:
«001706 201204 131920 122614 121308 260304 132003 001920 122614 171300 120413
191409»
Каждый из блоков возводим в квадрат по модулю 988027 и получаем:
«934382 619345 766849 374164 944753 268783 935864 722319 374164 276127 982371
376094»
Для расшифровки, например, первого блока поступаем так, как это описывалось выше. Число р, как легко проверяется, имеет вид р= 8m + 5, где m = 124. Поэтому
х 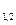 =
= 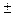 934382
934382 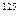 2
2 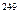 =
= 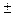 709 (mod 997).
709 (mod 997).
Число q имеет вид q = 4m + 3, где m = 247. Отсюда получаем
х 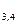 =
= 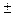 934382
934382  =
= 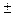 276 (mod 991).
276 (mod 991).
Дата добавления: 2016-07-22; просмотров: 1463;











