Определители матриц второго и третьего порядка

Каждой квадратной матрице А порядка n ставится в соответствие число, которое называется определителем этой матрицы. Обозначение: D, |A|, det A, .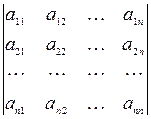

Определение 4.1. Определителем матрицы первого порядка А = (а₁₁) называется число а₁₁.

Пример 4.1. Например: если дана матрица первого порядка А = (3), то определитель этой матрицы |A| = 3.

Определение 4.2. Определителем матрицы второго порядка А = 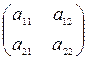называется число, которой находится по формуле: |A| = 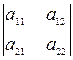= а₁₁а₂₂– а₁₂а₂₁.

Пример 4.2.Если дана матрица второго порядка А = 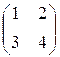, то определитель этой матрицы |A| = 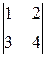= 1×4 – 2×3 = 4 – 6 = –2.

Определение 4.3. Определителем матрицы третьего порядка А = 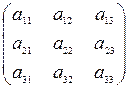называется число, которой находится по формуле: |A| = а₁₁а₂₂а₃₃ + а₁₂а₃₁а₂₃ + а₂₁а₁₃а₃₂ – а₁₃а₂₂а₃₁ – а₁₁а₃₂а₂₃ – а₃₃а₂₁а₁₂.

Это число состоит из шести слагаемых, в каждое слагаемое в качестве множителей входит по одному элементу из каждой строки и каждого столбца. Для запоминания формулы можно воспользоваться наглядным правилом знаков для выписывания произведений, входящих в разложение определителя третьего порядка. Схема на рис. 4.1 называется правилом треугольника или правилом Саррюса[10].

Правило составления выражения для определителя третьего порядка строится следующим образом. Из членов, входящих со знаком «+», один будет произведением элементов главной диагонали, каждый из двух других – произведением элементов, лежащих на параллели к этой диагонали, с добавлением третьего множителя из противоположного угла матрицы (рис. 4.1). Члены, входящие со знаком «–», строятся таким же, образом относительно другой диагонали.

Существует еще вторая схема правила Саррюса: к определителю приписывают справа два первых столбца и вычисляют сумму произведений элементов расположенных на главной диагонали и «прямых», параллельных ей, со знаком минус вычисляют сумму произведений элементов, расположенных на побочной диагонали, и «прямых», параллельных ей.

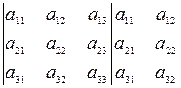= а₁₁а₂₂а₃₃ + а₁₂а₂₃а₃₁ + а₁₃а₂₁а₃₂ – а₁₃а₂₂а₃₁ – а₁₁а₂₃а₃₂ – а₁₂а₂₁а₃₃.

Пример 4.3. Если дана матрица третьего порядка А = 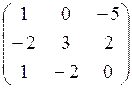, то определитель этой матрицы |A| = 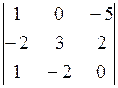= 1×3×0 + 1×0×2 + (–5)×(–2)×(–2) – (–5)×3×1 – 1×2×(–2) –
– 0×0×(–2) = –20 + 15 + 4 = –1.

4.2. Определитель матрицы n-го порядка

Для того чтобы дать определение определителя произвольного порядка, введем некоторые понятия. Пусть а_ij – элемент определителя порядка n, где i, j = 1, 2, …, n.

Определение 4.4. Минором элементаа_ij называется определитель M_ij, полученный из данного определителя вычеркиванием i-ой строки и j-го столбца.

Из определения следует, что минор элемента – это определитель
(n – 1) порядка.

Определение 4.5. Алгебраическим дополнением элемента а_ij называется его минор, взятый со знаком (–1)^{i + j}, т. е. А_ij = (–1)^{i + j}×M_ij.

Для определения понятия определителя n-го порядка воспользуемся индукцией по n, где n – порядок матрицы A.

Определение 4.6.

1. При n = 1 матрица А состоит из одного числа: |A| = а₁₁.

2. Пусть для матрицы порядка (n – 1) определитель известен.

3. Определителем матрицы А произвольного порядка n называется число, находящееся по формуле: |A| = 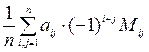, где суммирование распространяется на все элементы матрицы А.

Эта формула сводит вычисление определителей порядка n к вычислению определителей порядка (n – 1).