Понятие о чистом изгибе прямого бруса

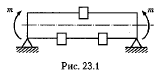Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент Деформация чистого изгиба будет, например, иметь место, ес­ли к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил.

На изгиб работают балки, оси,

валы и другие детали конструкций (определение балки известно из теоретической механики). В дальнейшем почти всегда мы будем рассматривать такие брусья, у которых имеется по крайней мере одна плоскость симметрии и плоскость действия нагрузок совпада­ет с ней. В этом случае деформация изгиба происходит в плоскости действия внешних сил и изгиб называется прямым в отличие от косого изгиба, рассматриваемого в подразд. 23.9.

При изучении деформации изгиба будем мысленно представ­лять себе, что балка состоит из бесчисленного количества волокон, параллельных оси. Для того чтобы получить представление о де­формации изгиба, проведем два опыта.

Балку, свободно лежащую на двух опорах, в верхней и нижней,
частях которой предварительно сделаны пазы и в них помещены
точно пригнанные по размеру пазов бруски, подвергнем деформа­ции изгиба (рис. 23.1). В результате этого бруски, расположенные
на выпуклой стороне, выпадут из пазов, а бруски, расположенные
на вогнутой стороне, будут зажаты.

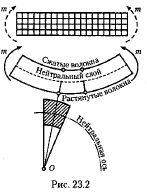
На боковую поверхность призматического резинового (для
большей наглядности) бруса прямоугольного сечения нанесем сет­ку продольных и поперечных прямых линий и подвергнем этот
брус деформации чистого изгиба (рис. 23.2). В результате можно
видеть следующее:

а)поперечные прямые линии
останутся при деформации пря­мыми, но повернутся навстречу друг к другу;

б)продольные прямые линии,
а также ось бруса искривятся;

в)сечения бруса расширятся
в поперечном направлении на во­гнутой стороне и сузятся на вы­пуклой стороне.

Из этих опытов можно сделать вывод, что при чистом изгибе справедлива гипотеза плоских се­чений; волокна, лежащие на выпуклой стороне, растягиваются, лежащие на вогнутой стороне — сжимаются, а на границе между ними лежит нейтральный слои волокон, которые только искривляются, не изменяя своей длины.

Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.

Искривление волокон и оси бруса происходит за счет неравно­мерного распределения нормальных напряжений по поперечному сечению.

Линия пересечения нейтрального слоя с плоскостью поперечно­го сечения называется нейтральной осью (и.о.). На ней­тральной оси нормальные напряжения равны нулю.

23.2. Изгибающий момент и поперечная сила

Как известно из теоретической механики, опорные реакции ба­лок определяют, составляя и решая уравнения равновесия статики для всей балки. Будем помнить, что при определении внутренних сил реакции связей учитываются наравне с активными внешними силами, действующими на балку.

Для определения внутренних силовых факторов применим ме­тод сечений, причем изображать балку будем только одной лини­ей — осью, к которой приложены активные и реактивные силы. Рассмотрим два случая.

1. К балке приложены две равные и противоположные по знаку пары сил (рис. 23.3).

Рассматривая равновесие части балки, расположенной слева или справа от сечения 1—1, видим, что во всех поперечных сечени­ях возникает только изгибающий момент М_и, равный внешнему моменту. Таким образом, это случай чистого изгиба.

Изгибающий момент есть результирующий момент относитель­но нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.

Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о не­пригодности правила знаков статики при определении знака изги­бающего момента.

2. К балке приложены активные и реактивные силы, перпенди­кулярные оси (рис. 23.4).

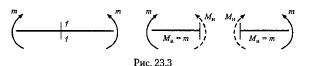
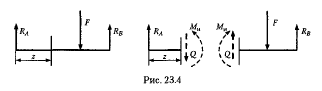
Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать из­гибающий момент М_и и поперечная сила Q. Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающе­му моменту, но и касательные, соответствующие поперечной силе.

Поперечная сила есть равнодействующая внутренних касатель­ных сил в поперечном сечении балки.

Обратим внимание на то, что поперечная сила имеет противопо­ложное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.

Изгиб, при котором в поперечном сечении балки действуют из­гибающий момент и поперечная сила, называется поперечным.

В общем, случае при поперечном изгибе изгибающий момент и поперечная сила в разных сечениях могут иметь неодинаковое зна­чение.

У балки, находящейся в равновесии под действием плоской сис­темы сил, алгебраическая сумма моментов всех активных и реак­тивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сече­ния, численно равна сумме моментов всех внешних сил, действую­щих на балку правее сечения.

Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяже­сти сечения всех внешних сил, действующих справа или слева от се­чения.

У балки, находящейся в равновесии под действием плоской сис­темы сил, перпендикулярных оси (т.е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следователь­но, сумма внешних сил, действующих на балку левее сечения, чис­ленно равна сумме сил, действующих на балку правее сечения.

Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.

Так как правила знаков статики неприемлемы для установле­ния знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно:

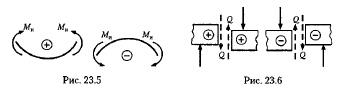
если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку вы­пуклостью вверх, то изгибающий момент в сечении считается от­рицательным (рис. 23.5);

если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая на­правлена вниз, то поперечная сила в сечении считается отрица­тельной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 23.6).

Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемленным, а связи отброшенными и замененными реакциями.

Подчеркнем, что для определения опорных реакций пользуются правилами знаков статики; для определения знаков изгибающего момента и поперечной силы — правилами знаков сопротивления материалов.

Правило знаков для изгибающих моментов иногда называют «правилом дождя» (имея в виду, что в случае выпуклости вниз образуется воронка, в которой задержится дождевая вода, и нао­борот).

23.3. Дифференциальные зависимости при изгибе

Между изгибающим моментом, поперечной силой и интенсив­ностью распределенной нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского, назван­ной по имени замечательного русского инженера-мостостроителя Д.И.Журавского (1821 — 1891). Эта теорема формулируется так; поперечная сила равна первой производной от изгибающего момен­та по абсциссе сечения балки.

Рассмотрим балку (рис. 23.7). Начало координат возьмем на ле­вом конце балки, а ось z направим вправо (в дальнейшем это будет иметь существенное значение).

На одном из участков балки возьмем сечение с текущей коорди­натой z и запишем уравнение изгибающего момента:

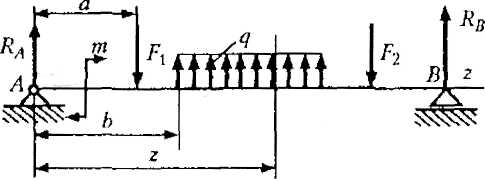
Рис. 23.7

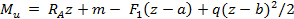
Продифференцировав это выражение по координате z получим

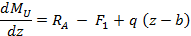
Выражение, стоящее в правой части этого равенства, есть попе­речная сила Q в сечении z. Таким образом, теорема доказана.

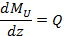
Если уравнение изгибающих моментов (для участков с равно­мерно распределенной нагрузкой) продифференцировать вторич­но, то получим

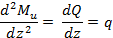
т.е. вторая производная от изгибающего момента или первая производная от поперечной силы по абсциссе сечения балки рав­на интенсивности распределенной нагрузки.

Как известно из высшей математики, по знаку второй производ­ной функции можно судить о выпуклости или вогнутости кривой; соответствующее правило следует использовать при построении эпюр.