Векторная диаграмма трансформатора
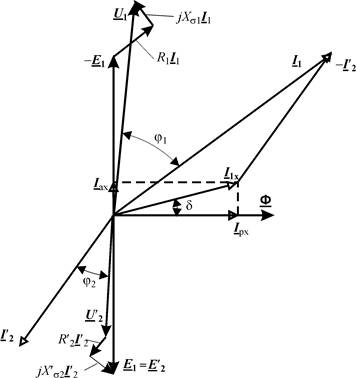 Уравнения Кирхгофа для цепей первичной и вторичной обмоток можно представить в графической форме в виде векторной диаграммы (рис. 1.4). Она позволяет наглядно представить соотношения между всеми величинами, определяющими работу трансформатора.
Уравнения Кирхгофа для цепей первичной и вторичной обмоток можно представить в графической форме в виде векторной диаграммы (рис. 1.4). Она позволяет наглядно представить соотношения между всеми величинами, определяющими работу трансформатора.
Построение диаграммы начинаем с вектора основного магнитного потока 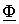 , который совмещаем с вещественной осью. Тогда вектор ЭДС первичной обмотки
, который совмещаем с вещественной осью. Тогда вектор ЭДС первичной обмотки 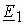 и равный ему вектор приведенной ЭДС вторичной обмотки
и равный ему вектор приведенной ЭДС вторичной обмотки 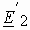 расположатся на мнимой отрицательной полуоси, т.к. ЭДС отстает от потока на
расположатся на мнимой отрицательной полуоси, т.к. ЭДС отстает от потока на 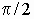 . Ток холостого хода
. Ток холостого хода 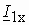 будет опережать вектор основного потока на угол магнитных потерь
будет опережать вектор основного потока на угол магнитных потерь 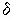 . Его реактивная
. Его реактивная 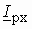 составляющая (ток намагничивания) совпадает с потоком, а активная составляющая
составляющая (ток намагничивания) совпадает с потоком, а активная составляющая 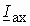 опережает поток на
опережает поток на 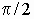 .
.
Для дальнейшего построения нужно определить характер нагрузки трансформатора. Если она активно-индуктивная, то ток вторичной обмотки 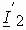 должен отставать от ЭДС
должен отставать от ЭДС 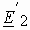 на некоторый угол в пределах от 0 до
на некоторый угол в пределах от 0 до 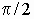 . Если активно-емкостная, то опережать ЭДС на угол в тех же пределах. Пусть нагузка активно-индуктивная. Тогда вектор
. Если активно-емкостная, то опережать ЭДС на угол в тех же пределах. Пусть нагузка активно-индуктивная. Тогда вектор 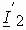 будет находиться в третьем квадранте.
будет находиться в третьем квадранте.
Пристроим к концу вектора 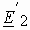 вектор
вектор 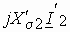 перпендикулярный вектору тока
перпендикулярный вектору тока 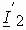 , а к его началу – вектор
, а к его началу – вектор 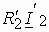 , совпадающий по направлению с током. В соответствии с уравнением Кирхгофа для цепи вторичной обмотки, вектор равный разности между
, совпадающий по направлению с током. В соответствии с уравнением Кирхгофа для цепи вторичной обмотки, вектор равный разности между 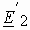 и
и 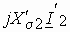 , а также
, а также 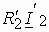 , будет вектором падения напряжения на нагрузке
, будет вектором падения напряжения на нагрузке 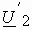 , т.е. его нужно провести из начала координат в точку начала вектора
, т.е. его нужно провести из начала координат в точку начала вектора 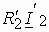 .
.
Для построения векторов уравнения первичной обмотки нужно определить вектор тока 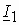 . Он равен разности между
. Он равен разности между 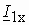 и
и 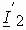 . Поэтому к концу вектора
. Поэтому к концу вектора 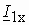 пристроим вектор
пристроим вектор 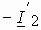 и получим
и получим 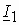 .
.
Теперь на положительной мнимой полуоси построим вектор 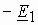 , а затем, пристроив к нему вектор
, а затем, пристроив к нему вектор 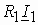 , совпадающий по направлению с
, совпадающий по направлению с 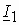 , и вектор
, и вектор 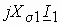 , перпендикулярный
, перпендикулярный 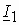 , получим точку конца вектора напряжения питания
, получим точку конца вектора напряжения питания 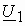 .
.
Дата добавления: 2016-06-29; просмотров: 2141;











