Гідродинаміка відцентрових насосів
Проточна порожнина всіх лопатевих насосів складається з трьох головних елементів – підводу, робочого колеса і відводу. Призначення робочого колеса – передача рідині енергії, яка підводиться до вала насоса. Робоче колесо складається з двох дисків, між якими знаходяться лопатки. Лопатки загнуті назад за напрямом обертання колеса і утворюють проточні канали. Звичайно робочі колеса виливають як одне ціле з лопатками. Лопаток в колесі є від 6 до 12, найчастіше 6....8, рідко менше 6.В залежності від входу рідини в канали робочого колеса відрізняють робочі колеса з одностороннім та двостороннім входом.
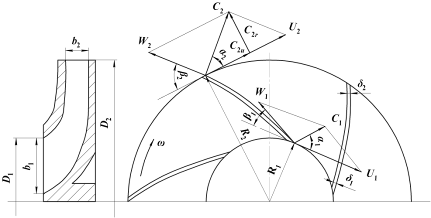
Геометричні розміри робочого колеса з одностороннім входом, від яких залежать його параметри роботи, показано на рисунку 1.4.
Робоче колесо характеризується не тільки числом лопаток 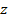 , але й напрямом їх крутизни відносно напрямку обертання. В залежності від величини кута
, але й напрямом їх крутизни відносно напрямку обертання. В залежності від величини кута 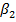 розрізняють радіальні лопатки (
розрізняють радіальні лопатки ( 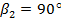 ), відігнуті вперед (
), відігнуті вперед ( 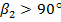 ) та загнуті назад (
) та загнуті назад ( 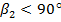 ).
).
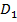 – діаметр входу в колесо;
– діаметр входу в колесо; 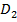 – діаметр колеса на виході;
– діаметр колеса на виході; 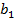 і
і 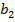 – відповідно ширина міжлопаткових каналів на вході і виході з колеса;
– відповідно ширина міжлопаткових каналів на вході і виході з колеса; 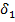 і
і 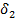 – відповідно товщина лопатки на вході і виході з колеса;
– відповідно товщина лопатки на вході і виході з колеса; 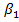 і
і 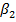 – відповідно кут нахилу лопатки на вході і виході з колеса, приймається
– відповідно кут нахилу лопатки на вході і виході з колеса, приймається 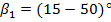 ,
, 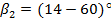
Рисунок 1.4 – Основні розміри робочого колеса і плани швидкостей на його вході і виході
Рух в’язкої рідини в каналах робочого колеса має складний характер. Рідина, яка знаходиться під дією масових і поверхневих сил, утворює в колесі тримірний потік з нестійким приграничним шаром, а це викликає вторинну течію. Сили Коріоліса і відцентрові сили, які виникають в результаті обертання колеса, викликають нерівномірний розподіл швидкостей в перерізі колеса. Вивчення такого руху є складною задачею гідродинаміки. В інженерній практиці ця задача рішається спрощено на основі теорії Ейлера, при цьому враховуються наступні припущення:
1) рідина рахується ідеальною;
2) по ширині каналу при відносному русі швидкості приймаються однаковими;
3) рух приймається усталеним.
Такий рух ідеальної рідини можливий в колесі з безмежно великим числом лопаток ( 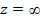 ). При таких умовах канали будуть такими малими, що рух в них можна вважати струминним.
). При таких умовах канали будуть такими малими, що рух в них можна вважати струминним.
На рисунку 1.4 з врахуванням вище викладеного показані паралелограми швидкостей на вході і виході з лопатки при постійній частоті обертання 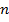 . При цьому прийнято наступні умовні позначення: індекс 1 відноситися до входу на лопатку колеса, індекс 2 – до виходу з колеса,
. При цьому прийнято наступні умовні позначення: індекс 1 відноситися до входу на лопатку колеса, індекс 2 – до виходу з колеса, 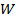 – вектор відносної швидкості,
– вектор відносної швидкості, 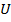 – вектор переносної (колової) швидкості,
– вектор переносної (колової) швидкості, 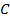 – вектор абсолютної швидкості,
– вектор абсолютної швидкості, 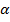 – кут між векторами абсолютної і колової швидкості.
– кут між векторами абсолютної і колової швидкості.
Звичайно в насосах 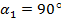 , а
, а 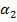 знаходяться в межах від
знаходяться в межах від 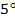 до
до 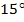 .
.
Для кожного відцентрового насоса існує режим ( 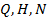 ), при якому внутрішні втрати в насосі мінімальні , а його ККД має найбільше числове значення. Такий режим називається оптимальним (номінальним).
), при якому внутрішні втрати в насосі мінімальні , а його ККД має найбільше числове значення. Такий режим називається оптимальним (номінальним).
За відомими геометричними характеристиками робочого колеса при постійній частоті його обертання можна аналітичним методом визначити параметри оптимального режиму роботи насоса. Крім цього, за розмірами робочого колеса можна визначити належність відцентрового насоса до того чи іншого типу, а за коефіцієнтом швидкохідності оцінити межі можливого раціонального використання насоса.
Величина коефіцієнта швидкохідності визначається як:
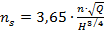 , ,
| (1.21) |
де 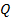 – витрата, м3/с;
– витрата, м3/с;
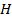 – напір, м;
– напір, м;
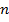 – частота обертання ротора, об/хв.
– частота обертання ротора, об/хв.
У додатку 9 приведено зв’язок параметрів насосу з коефіцієнтом швидкохідності.
Теоретичний напір насоса (рівняння Ейлера):
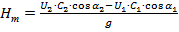 . .
| (1.22) |
Оскільки переважно у насосах 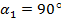 , а також, вводячи поправочний коефіцієнт
, а також, вводячи поправочний коефіцієнт 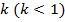 , отримаємо формулу для напору насосу:
, отримаємо формулу для напору насосу:
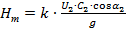
| (1.23) |
або
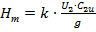 , ,
| (1.24) |
де 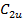 – дотична складова абсолютної швидкості на виході із робочого колеса,
– дотична складова абсолютної швидкості на виході із робочого колеса, 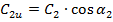 .
.
 Коефіцієнт
Коефіцієнт 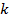 , що враховує остаточну кількість лопаток робочого колеса визначається за формулою
, що враховує остаточну кількість лопаток робочого колеса визначається за формулою 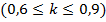 :
:
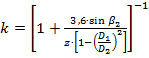 . .
| (1.25) |
Колова швидкість на вході і виході робочого колеса, відповідно:
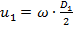 , ,
| (1.26) |
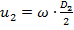 , ,
| (1.27) |
де 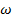 – кутова швидкість обертання робочого колеса:
– кутова швидкість обертання робочого колеса:
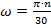 . .
| (1.28) |
Якщо припустити, що на вході в колесо відсутнє закручування потоку, то радіальна швидкість на вході дорівнює абсолютній швидкості:
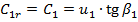 . .
| (1.29) |
Дотична складова абсолютної швидкості на виході із робочого колеса:
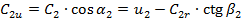 , ,
| (1.30) |
де 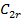 – радіальна швидкість на виході з робочого колеса для визначення якої треба провести наступні розрахунки.
– радіальна швидкість на виході з робочого колеса для визначення якої треба провести наступні розрахунки.
Визначимо коефіцієнти стиснення 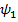 та
та 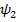 відповідно на вході та виході колеса:
відповідно на вході та виході колеса:
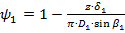 , ,
| (1.30) |
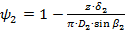 . .
| (1.31) |
Теоретична подача при оптимальному режимі:
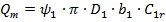 . .
| (1.32) |
Тоді радіальна швидкість на виході із колеса визначається за формулою:
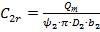 . .
| (1.33) |
За приведеними формулами будуються трикутники швидкості на вході в робоче колесо та на виході із нього (рисунок 1.4).
Визначаємо оптимальну потужність насоса з врахуванням механічного ККД 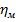 (див. додаток 9):
(див. додаток 9):
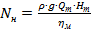 , ,
| (1.34) |
де 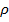 – густина продукту.
– густина продукту.
Із рівняння Ейлера виведена формула залежності теоретичного напору від подачі:
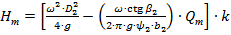 . .
| (1.35) |
Враховуючи, що:
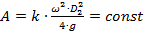 , ,
| (1.36) |
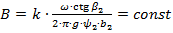 , ,
| (1.37) |
характеристика буде мати вигляд:
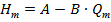 . .
| (1.38) |
На рисунку 1.5 приведена теоретична характеристика насоса.
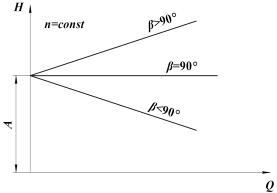
Рисунок 1.5 – Теоретичні характеристики
відцентрових машин при різних кутах 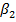
Теоретична потужність визначається за формулою:
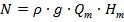 . .
| (1.38) |
Приклад 1.2
Для насоса з числом лопаток 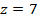 , діаметром входу в колесо
, діаметром входу в колесо 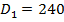 мм та виходу
мм та виходу 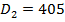 мм, шириною міжлопаткових каналів на вході
мм, шириною міжлопаткових каналів на вході 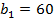 мм та на виході
мм та на виході 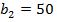 мм, кутом нахилу лопаток на вході
мм, кутом нахилу лопаток на вході 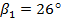 та на виході
та на виході 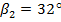 , товщиною лопаток на вході
, товщиною лопаток на вході 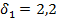 мм та на виході
мм та на виході 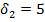 мм, побудувати трикутники швидкості рідини на вході і на виході, а також теоретичну характеристику насоса. Частота обертання колеса
мм, побудувати трикутники швидкості рідини на вході і на виході, а також теоретичну характеристику насоса. Частота обертання колеса 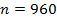 об/хв, густина рідини, що перекачується
об/хв, густина рідини, що перекачується 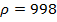 кг/м3.
кг/м3.
Розв’язок
Визначаємо коефіцієнти стиснення на вході та виході колеса відповідно за формулами (1.30) та (1.31):
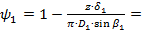 .
. 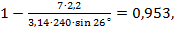
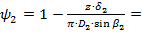 .
. 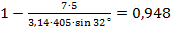 .
.
Кутова швидкість обертання робочого колеса згідно формули (1.28) складає:
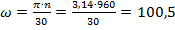 с-1.
с-1.
Визначаємо колові швидкості на вході та виході колеса за формулами (1.26) і (1.27):
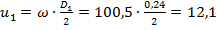 м/с,
м/с,
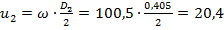 м/с.
м/с.
Радіальну швидкість рідини на вході визначимо за формулою (1.29):
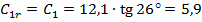 м/с.
м/с.
Теоретичну подачу насоса при оптимальному режимі визначаємо за формулою (1.32):
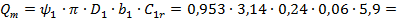
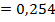 м3/с.
м3/с.
Радіальна швидкість на виході із колеса визначається за формулою (1.33):
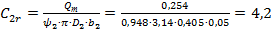 м/с.
м/с.
Дотична складова абсолютної швидкості на виході із робочого колеса визначається за формулою (1.30):
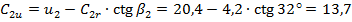 м/с.
м/с.
За формулою (1.25) визначаємо поправку, що враховує остаточну кількість лопаток робочого колеса:
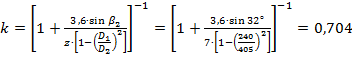 .
.
Теоретичний напір визначаємо за формулою (1.24):
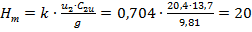 м.
м.
Визначимо коефіцієнт швидкості за формулою (1.21):
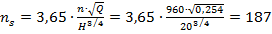 .
.
За додатком 9, при 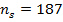 та при
та при 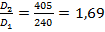 вибираємо механічний ККД
вибираємо механічний ККД 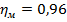 .
.
Номінальну потужність насоса визначаємо за формулою (1.34):
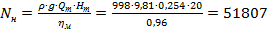 Вт.
Вт.
Визначимо коефіцієнти 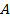 і
і 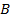 відповідно за формулами (1.36) та (1.37):
відповідно за формулами (1.36) та (1.37):
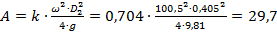 м,
м,
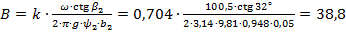 с2/м5.
с2/м5.
Підставивши значення 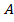 і
і 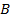 в рівняння (1.38) отримаємо математичну модель теоретичної характеристики насоса:
в рівняння (1.38) отримаємо математичну модель теоретичної характеристики насоса:
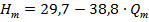 .
.
Тепер, задаючись шістьма значеннями подачі  в межах від
в межах від 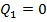 до
до 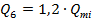 , визначимо:
, визначимо:
- значення теоретичного напору при подачі  :
:
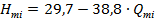 ;
;
- значення теоретичної потужності при подачі  :
:
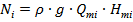 .
.
Розрахунок зводимо в таблицю 1.4.
Таблиця 1.4 – Розрахункові дані для побудови характеристики
| Подача Qі, м3/с | 0,06 | 0,12 | 0,18 | 0,24 | 0,30 | |
| Напір Hі, м | 29,7 | 27,4 | 25,1 | 22,7 | 20,4 | 18,1 |
| Потужність Nі, Вт | – |
За результатами розрахунків будуємо трикутники швидкостей на вході і виході (рисунок 1.6) та теоретичну характеристику насоса (рисунок 1.7).
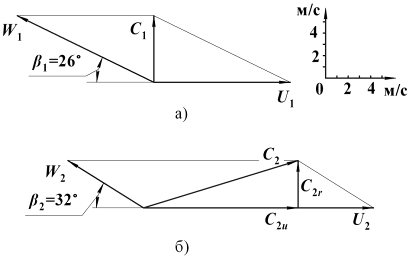
а) – на вході в робоче колесо; б) – на виході з робочого колеса
Рисунок 1.6 – Трикутники швидкостей насоса
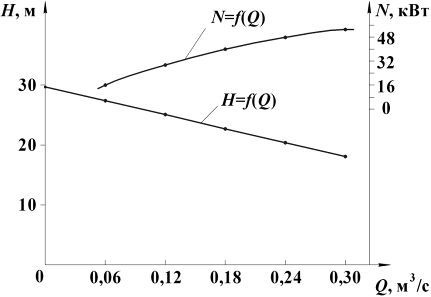
Рисунок 1.7 – Теоретична характеристика насоса
Дата добавления: 2016-06-29; просмотров: 2553;











