Интерполяционные многочлены Лагранжа
Численная интерполяция
Постановка задачи
Пусть в точках x0, x1, ..., xn таких, что a £ x0 < … < xn £ b, известны значения функции у = f(x), т.е. на отрезке [а, b] задана табличная (сеточная) функция
| x | x0 | x1 | … | xn | (1) |
| y | y0 | y1 | … | yn |
Функция φ(x) называется интерполирующей или интерполяционной для f(x) на [а, b], если ее значения j(x0), φ(x1), …, φ(xn) в заданных точках х0, х1, ..., xn, называемых узлами интерполяции, совпадают с заданными значениями функции f(x), т. е. с у0, у1, ..., уn соответственно. Геометрически факт интерполирования означает, что график функции j(x) проходит так, что, по меньшей мере, в n + 1 заданных точках он пересекает или касается графика функции f(x) (Рис. 1).
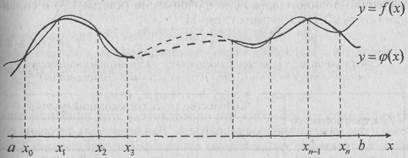
Рис. 1. Геометрическая интерпретация задачи интерполирования
Легко представить, что таких графиков φ(x), проходящих через заданные точки, можно изобразить сколько угодно, и они могут отличаться от графика f(x) сколь угодно сильно, если не накладывать на φ(x) и f(x) определенных ограничений.
В соответствии с договоренностью предыдущего параграфа будем считать, что интерполяционная функция φ(x) есть многочлен степени n. Тогда задача интерполяции, точнее, полиномиальной, алгебраической или параболической интерполяции (поскольку график любого многочлена называют параболой) формулируется так: для функции f(x), заданной таблицей (1), найти многочлен Рn(x) такой, что выполняется совокупность условий интерполяции
Pn(xi) = yi "i Î {0, 1, …, n} (2)
Найти многочлен Pn(x) — это значит, учитывая его каноническую форму
Рn(x) = a0 + a1x + a2x2 + ... + anxn, (3)
найти его n + 1 коэффициент a0, a1, …, an. Для этого имеется как раз n + 1 условие (2). Таким образом, чтобы многочлен (3) был интерполяционным для функции (1), нужно, чтобы его коэффициенты a0, a1, …, an удовлетворяли системе уравнений
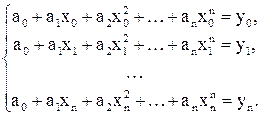
Из курса алгебры известно, что определитель этой линейной системы (так называемый определитель Вандермонда) отличен от нуля, т. е. решение этой системы существует и единственно. Однако практическое построение интерполяционного многочлена таким путем малоэффективно. Поэтому изберем другой путь.
Интерполяционные многочлены Лагранжа
Будем строить многочлен n-й степени Ln(x) в виде линейной комбинации 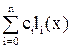 многочленов n-й же степени li(x) (i = 0, 1, ..., n). Для того чтобы такой многочлен был интерполяционным для функции f(x), достаточно зафиксировать в качестве коэффициентов сi этой линейной комбинации заданные в табл. (1) значения yi = f(xi), а от базисных многочленов li(x) потребовать выполнения условия
многочленов n-й же степени li(x) (i = 0, 1, ..., n). Для того чтобы такой многочлен был интерполяционным для функции f(x), достаточно зафиксировать в качестве коэффициентов сi этой линейной комбинации заданные в табл. (1) значения yi = f(xi), а от базисных многочленов li(x) потребовать выполнения условия
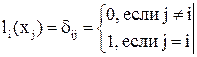 "j, i Î {0, 1, …, n}. (4)
"j, i Î {0, 1, …, n}. (4)
В таком случае для многочлена
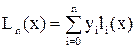
в каждом узле xj (j Î {0, 1, …, n}), в силу (4), справедливо
Ln(xj) = l0(xj)y0 + … + lj–1(xj)yj–1 + lj(xj)yj + lj+1(xj)yj+1 + … + ln(xj)yn =
= 0 + … + yj + 0 + ... + 0 = yj,
т.е. выполняются условия интерполяции (2).
Чтобы конкретизировать базисные многочлены li(x), учтем, что они должны удовлетворять условиям (4). Равенство нулю i-го многочлена во всех узлах, кроме i-го, означает, что li(x) можно записать в виде
li(x) = Ai(x – x0)...(x – xi–1)(x – xi+1)...(x – xn),
а коэффициент Ai этого представления легко получается из содержащегося в (4) требования li(xi) = 1. Подставляя в выражение li(x) значение x = xi и приравнивая результат единице, получаем
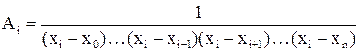 .
.
Таким образом, базисные многочлены Лагранжа имеют вид
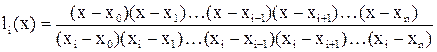 ,
,
а искомый интерполяционный многочлен Лагранжа есть
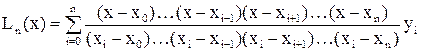 . (5)
. (5)
Заметим, что числитель, фигурирующий в записи i-го слагаемого Ln(x) дроби, представляет собой произведение разностей между переменной x и всеми узлами, кроме i-го, а знаменатель — произведение разностей между i-м узлом и всеми остальными.
Будем выяснять величину отклонения f(x) от Ln(x) в произвольной точке x Î [a; b], иначе, величину остаточного члена
Rn(x) = f(x) – Ln(x)
интерполяционной формулы Лагранжа в предположении, что 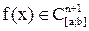 , т. е. данная функция n + 1 раз непрерывно дифференцируема. Обозначим
, т. е. данная функция n + 1 раз непрерывно дифференцируема. Обозначим
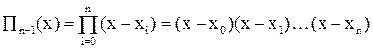 — (6)
— (6)
определенный через узлы x1, x2, ..., xn многочлен (n + 1)-й степени. Через него введем в рассмотрение функцию
u(x) = f(x) – Ln(x) – cПn+1(x), (7)
где c — некоторая постоянная (параметр).
Так как в точках x = x0, x1, ..., xn многочлен Пn+1(x) обращается в нуль, согласно его конструкции, a f(x) – Ln(x) = 0 в этих точках по условиям интерполяции, то и u(xi) = 0 при i = 0, 1, …, n, т.е. функция u(x) имеет на отрезке [а; b] по меньшей мере n + 1 корень. Подберем параметр с так, чтобы u(x) имела заведомо еще и (n + 2)-й корень в какой-то фиксированной точке 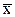 (¹ xi) промежутка [а; b]. Имеем:
(¹ xi) промежутка [а; b]. Имеем:
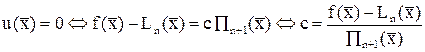 ,
,
причем такое значение c обязательно найдется, поскольку Πn+1(x) = 0 только в узлах xi.
Пусть для определенности 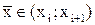 . Тогда можно утверждать, что при найденном с функция u(x) равна нулю на концах n + 1 отрезков [x0; x1], [х1; х2], ..., [xi;
. Тогда можно утверждать, что при найденном с функция u(x) равна нулю на концах n + 1 отрезков [x0; x1], [х1; х2], ..., [xi; 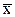 ], [
], [ 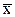 ; xi+1], ..., [xn-1; xn]. Значит, к функции u(x) на каждом из этих отрезков применима теорема Ролля, т.е. внутри каждого из этих отрезков существует, по крайней мере, по одной такой точке, в которой производная функции u(x) обращается в нуль. Эти n + 1 точки образуют систему из n отрезков, на концах каждого из которых уже функция u'(x) равна нулю, т.е. теперь к производной можно применить теорему Ролля, по которой существует n нулей второй производной функции u(x). Продолжая процесс таких рассуждений далее, в конце концов, приходим к выводу о существовании такой точки ξ Î (x0; xn) Ì (a; b), что u(n+1)(ξ) = 0. Учитывая, что n-я производная многочлена n-й степени постоянна, а (n + 1)-я равна нулю, находим выражение (n + 1)-й производной функции u(x), заданной равенством (7):
; xi+1], ..., [xn-1; xn]. Значит, к функции u(x) на каждом из этих отрезков применима теорема Ролля, т.е. внутри каждого из этих отрезков существует, по крайней мере, по одной такой точке, в которой производная функции u(x) обращается в нуль. Эти n + 1 точки образуют систему из n отрезков, на концах каждого из которых уже функция u'(x) равна нулю, т.е. теперь к производной можно применить теорему Ролля, по которой существует n нулей второй производной функции u(x). Продолжая процесс таких рассуждений далее, в конце концов, приходим к выводу о существовании такой точки ξ Î (x0; xn) Ì (a; b), что u(n+1)(ξ) = 0. Учитывая, что n-я производная многочлена n-й степени постоянна, а (n + 1)-я равна нулю, находим выражение (n + 1)-й производной функции u(x), заданной равенством (7):
u(n+1)(x) = f(n+1)(x) – 0 – c(n + 1)!.
Итак, существует точка ξ Î (x0; xn) такая, что
f(n+1)(ξ) – 0 – c(n + 1)! = 0, т. е. 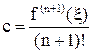 .
.
Это значение с должно совпадать с выбранным ранее, т.е. должно выполняться равенство
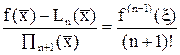 ,
,
откуда получаем
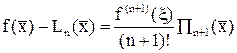 .
.
Так как в качестве  могла быть взята любая точка x из промежутка [а; b], не совпадающая ни с какой узловой, расфиксируем (или, как еще говорят, разморозим) точку
могла быть взята любая точка x из промежутка [а; b], не совпадающая ни с какой узловой, расфиксируем (или, как еще говорят, разморозим) точку  , т.е. заменим ее в последнем равенстве произвольной точкой x ¹ xi, в результате чего приходим к выражению остаточного члена
, т.е. заменим ее в последнем равенстве произвольной точкой x ¹ xi, в результате чего приходим к выражению остаточного члена
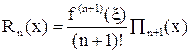 . (8)
. (8)
Знание остаточного члена в предположении (n + 1)-кратной дифференцируемости f(x) позволяет записать точное представление f(x) через ее интерполяционный многочлен Ln(x):
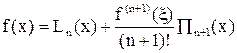 , (9)
, (9)
где ξ — некоторая (вообще говоря, неизвестная, причем зависящая от x) точка из промежутка интерполяции (а; b), а Пn+1(x) — определенный в (6) многочлен.
Теперь можно ставить и пытаться отвечать на вопросы о погрешности приближенного вычисления значения f(x) с помощью Ln(x) в какой-либо конкретной точке промежутка [а; b], о величине максимальной погрешности, допускаемой при подмене функции f(x) многочленом Ln(x) на этом промежутке, о сходимости интерполяционного процесса, т. е. о том, имеет ли место 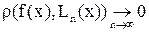 по метрике r(·,·) того или иного определенного на [a; b] функционального пространства. Так, если известна величина
по метрике r(·,·) того или иного определенного на [a; b] функционального пространства. Так, если известна величина
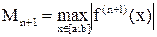 ,
,
то оценить абсолютную погрешность интерполяционной формулы f(x) » Ln(x) в любой точке 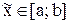 можно с помощью неравенства
можно с помощью неравенства
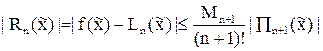 . (10)
. (10)
Максимальная погрешность интерполирования на отрезке [а; b] оценивается величиной
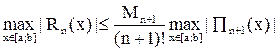 (11)
(11)
Дата добавления: 2022-04-12; просмотров: 259;











