Производная скалярного поля по направлению.
Рассмотрим 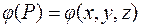 .
.
Частные производные функции 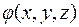 :
: 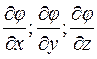 – определяют скорость изменения скалярного поля по направлениям координатных осей.
– определяют скорость изменения скалярного поля по направлениям координатных осей.
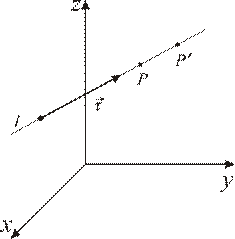
Рис. 9.2
Рассмотрим произвольное направление 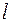 в пространстве, определяемое направляющим вектором
в пространстве, определяемое направляющим вектором 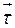 единичной длины
единичной длины 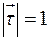 (см. рис. 9.2). Определим скорость изменения скалярного поля
(см. рис. 9.2). Определим скорость изменения скалярного поля 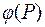 в направлении
в направлении  . Пусть точки
. Пусть точки 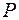 и
и 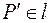 .
.
Производной скалярного поля 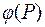 в точке
в точке 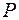 по направлению прямой
по направлению прямой 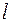 назовем следующий предел:
назовем следующий предел:
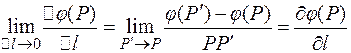 ,
,
где 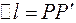 берется со знаком «+», если направление
берется со знаком «+», если направление  совпадает с направлением
совпадает с направлением 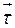 , и со знаком «-» в противоположном случае. Пусть
, и со знаком «-» в противоположном случае. Пусть 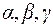 – углы, образованные прямой
– углы, образованные прямой 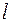 с осями координат
с осями координат 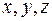 , тогда вектор
, тогда вектор 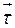 имеет координаты:
имеет координаты:
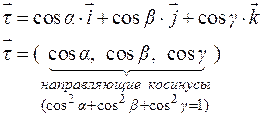
Пусть 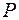 имеет координаты
имеет координаты 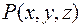 , а
, а 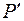 – координаты
– координаты 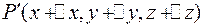
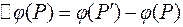
Запишем приращение 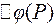 в виде:
в виде:
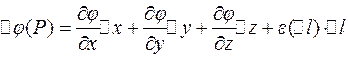 ,
,
где 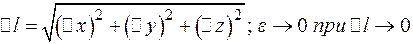 , т.к.
, т.к. 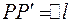 , то
, то
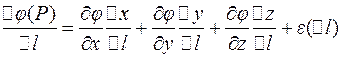
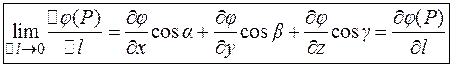
Пример:
Вычислить производную поля в точке 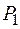 по направлению
по направлению 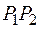 , если
, если
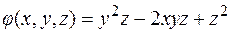
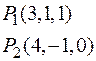
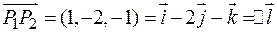
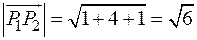 – длина вектора
– длина вектора 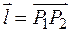
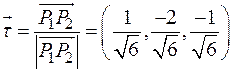 – единичный вектор направления
– единичный вектор направления  .
.
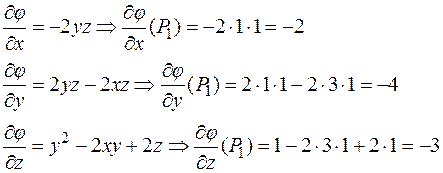
Вычислим скалярное произведение векторов 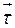 и
и 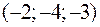 :
:
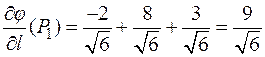
Оказалось, что
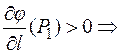 в этом направлении скалярное поле возрастает.
в этом направлении скалярное поле возрастает.
Градиент скалярного поля.
Рассмотрим формулу для вычисления производной по направлению
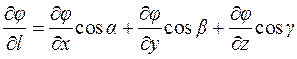
Формула имеет вид скалярного произведения вектора 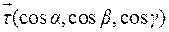 и вектора с координатами
и вектора с координатами 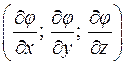 .
.
Определение.
Вектор с координатами 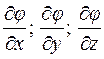 называется градиентом функции
называется градиентом функции 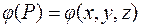 в точке
в точке 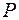 и обозначается:
и обозначается:
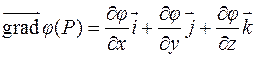
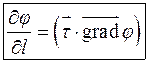
Свойства градиента:
1. 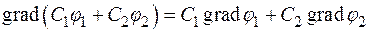
2. 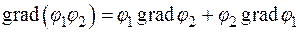
3. 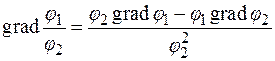
4. 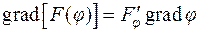
Введем дифференциальный оператор «набла»
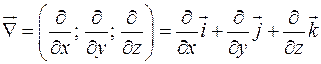
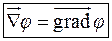
Свойства оператора «набла» повторяют свойства градиента.
9.2. Связь вектора градиента с производной по направлению
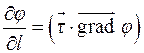
Если обозначить через 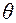 угол между вектором-градиентом и единичным вектором
угол между вектором-градиентом и единичным вектором 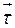 , то
, то
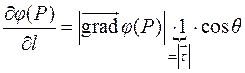 (по определению скалярного произведения
(по определению скалярного произведения 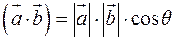 )
)
Производная поля 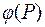 по направлению
по направлению 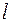 , определяющая скорость роста в этом направлении, будет максимальна, если
, определяющая скорость роста в этом направлении, будет максимальна, если 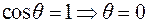 . Т.е. когда направление вектора
. Т.е. когда направление вектора 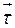 совпадает с направлением вектора градиента. Обозначим через
совпадает с направлением вектора градиента. Обозначим через 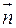 это направление максимальной скорости изменения функции:
это направление максимальной скорости изменения функции:
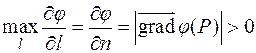
(максимально по всем направлениям)
Пример:
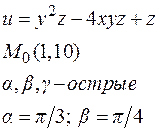
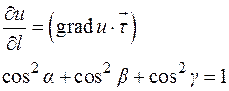
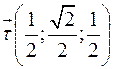
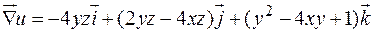
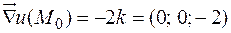
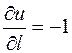
9.3. Теорема об ортогональности вектора градиента поверхности уровня

Рис. 9.3
Вектор градиент в каждой точке  скалярного поля
скалярного поля  направлен ортогонально касательной плоскости, проведенной в данной точке
направлен ортогонально касательной плоскости, проведенной в данной точке 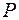 к поверхности уровня, проведенной через
к поверхности уровня, проведенной через 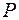 (см. рис. 9.3).
(см. рис. 9.3).
Доказательство:
Проведем на касательной плоскости 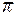 произвольную прямую l, проходящую через
произвольную прямую l, проходящую через 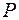 . На поверхности уровня проведем линию
. На поверхности уровня проведем линию 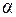 через
через 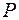 так, что l направлена по касательной к
так, что l направлена по касательной к 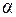 . Кривую
. Кривую 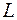 в пространстве зададим вектор-функцией:
в пространстве зададим вектор-функцией:
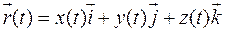
То, что 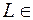 поверхности уровня
поверхности уровня 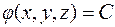 означает, что координаты кривой
означает, что координаты кривой 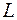
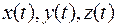 удовлетворяют уравнению поверхности уровня
удовлетворяют уравнению поверхности уровня 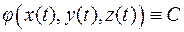 .
.
Продифференцируем это тождество:
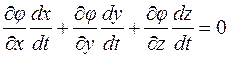 .
.
Это равенство можно переписать как скалярное произведение векторов:
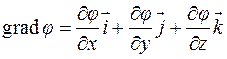 и
и
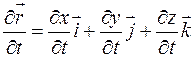
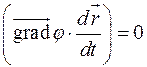
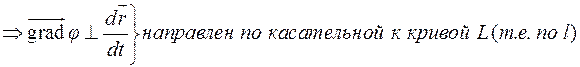
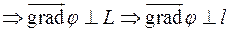 ,
,
т.к. 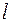 – произвольная прямая, то
– произвольная прямая, то 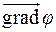 будет ортогонален любой прямой, проходящей через т.
будет ортогонален любой прямой, проходящей через т. 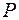 и лежащей в касательной плоскости
и лежащей в касательной плоскости 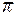 , т.е.
, т.е.
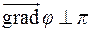 .
.
Нормаль к поверхности.
Нормалью к поверхности называется вектор, ортогональный касательной плоскости, проведенной к данной поверхности в данной точке. Выше доказано, что по нормали к поверхности 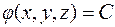 направлен вектор
направлен вектор 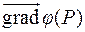 .
.
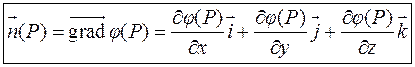
Единичный вектор нормали к поверхности находится делением градиента на его длину
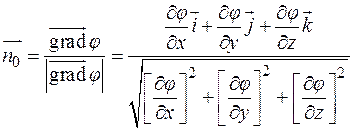
Пример:
Найти единичный вектор нормали к поверхности 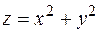 в точке
в точке 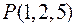 . Указанная поверхность является параболоидом вращения (см. рис. 9.4).
. Указанная поверхность является параболоидом вращения (см. рис. 9.4).

Рис. 9.4
Перепишем уравнение параболоида в виде:
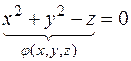
Тогда:
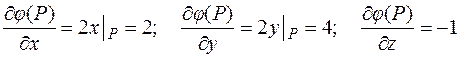
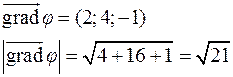
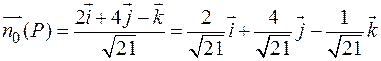
Инвариантность вектора градиента.
Градиент скалярного поля есть вектор, направленный в любой точке поля в сторону роста значений скалярного поля по направлению наибольшей скорости этого роста. Длина вектора градиента в любой точке равна наибольшей скорости изменения поля в этой точке.
Градиент – вектор, длина и направление которого определены для заданного поля 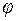 в заданной точке
в заданной точке 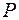 , т.е. является характеристикой поля и не зависит от системы координат.
, т.е. является характеристикой поля и не зависит от системы координат.
Вывод: вектор 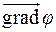 скалярного поля, является характеристикой поля, инвариантен по отношению к выбору системы координат.
скалярного поля, является характеристикой поля, инвариантен по отношению к выбору системы координат.
9.4. Векторные поля. Основные понятия.
Определение векторного поля.
В области 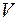 пространства задано векторное поле, если любой точке
пространства задано векторное поле, если любой точке 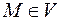 поставлен в соответствие вектор
поставлен в соответствие вектор 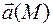 .
.
Примеры векторных полей:
Поле тяготения, поле скоростей движения жидкости, поле электрической или магнитной напряженности, и т.п.
В декартовой системе точка 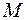 имеет координаты
имеет координаты 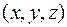 , а вектор
, а вектор 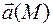 в координатной форме будет иметь вид:
в координатной форме будет иметь вид:
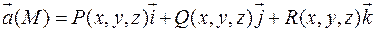
Т.е. задание векторного поля в пространстве эквивалентно заданию трех функций 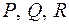 от трех переменных в области
от трех переменных в области 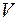 .
.
Будем в дальнейшем предполагать, что все эти функции непрерывныв вместе с частными производными. Так как каждый вектор характеризуется величиной и направлением, то задание в
вместе с частными производными. Так как каждый вектор характеризуется величиной и направлением, то задание в 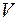 векторного поля означает задание в
векторного поля означает задание в 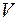 поля длин и поля направлений. В качестве геометрической характеристики векторного поля направлений можно ввести понятие векторных линий поля.
поля длин и поля направлений. В качестве геометрической характеристики векторного поля направлений можно ввести понятие векторных линий поля.
Определение.
Векторной линией векторного поля 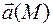 назовем всякую линию, которая в каждой своей точке касается векторов векторного поля
назовем всякую линию, которая в каждой своей точке касается векторов векторного поля 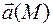 .
.

Рис. 9.5
Запишем уравнение векторных линий (см. рис. 9.5):
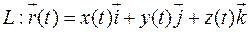
Производная 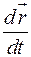 – вектор, направленный в каждой точке кривой по касательной к ней. Следовательно, чтобы
– вектор, направленный в каждой точке кривой по касательной к ней. Следовательно, чтобы 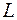 была векторной линией векторного поля
была векторной линией векторного поля 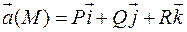 нужно, чтобы векторы
нужно, чтобы векторы 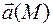 и
и 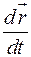 были коллинеарны, т.е.
были коллинеарны, т.е.
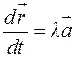
или в координатной форме:
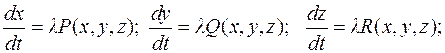
после исключения коэффициента 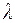 :
:
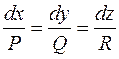
Эта система дифференциальных уравнений после интегрирования дает уравнения векторных линий поля. Отметим, что в силу условий, наложенных на функции 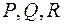 (непрерывные, с непрерывными частными производными) выполнена теорема существования и единственности решения, т.е. через любую точку
(непрерывные, с непрерывными частными производными) выполнена теорема существования и единственности решения, т.е. через любую точку 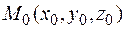 области
области 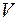 проходит единственная векторная линия, являющаяся интегральной кривой системы.
проходит единственная векторная линия, являющаяся интегральной кривой системы.
Пример:
Поле напряженности магнитного поля 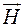 , создаваемого электрическим током силы
, создаваемого электрическим током силы 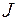 , текущим по бесконечному проводнику, будет плоским. Если выбрать систему координат так, чтобы проводник располагался внутри оси
, текущим по бесконечному проводнику, будет плоским. Если выбрать систему координат так, чтобы проводник располагался внутри оси 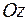 , то в каждой плоскости
, то в каждой плоскости 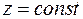 поле будет одинаковым
поле будет одинаковым
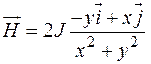
Тогда с точностью до множителя 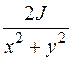 поле имеет вид
поле имеет вид
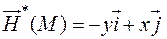 ,
,
т.е. 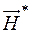 коллинеарно
коллинеарно 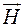 .
.
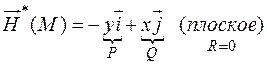
Запишем уравнение векторных линий для поля 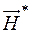 :
:
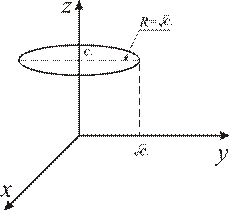
Рис. 9.6
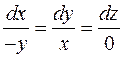 или
или
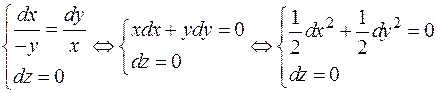
Интегрирование этой системы дает следующий вид векторных или силовых линий поля:
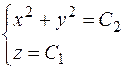 – окружности в плоскостях
– окружности в плоскостях 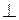 оси
оси 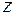 .
.
(см. рис. 9.6)
Введем в рассмотрение понятие векторной трубки, помещенной в векторное поле. В область 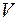 заданного векторного поля
заданного векторного поля 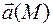 поместим замкнутый контур
поместим замкнутый контур 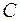 и через точки контура проведем векторные линии. Образуется некоторая поверхность, которую и будем называть векторной трубкой. Поверхность
и через точки контура проведем векторные линии. Образуется некоторая поверхность, которую и будем называть векторной трубкой. Поверхность  , натянутую на контур
, натянутую на контур 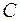 , назовем сечением трубки. Любая векторная линия
, назовем сечением трубки. Любая векторная линия 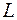 , вошедшая в векторную трубку через сечение
, вошедшая в векторную трубку через сечение 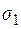 , может выйти из нее только через другое сечение
, может выйти из нее только через другое сечение 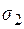 , т.е. векторная линия
, т.е. векторная линия 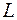 не может пересечь боковую поверхность векторной трубки. Если это допустить, то через точку боковой поверхности пройдут две векторные линии:
не может пересечь боковую поверхность векторной трубки. Если это допустить, то через точку боковой поверхности пройдут две векторные линии: 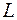 и образующая трубки. А это противоречит теореме единственности векторных линий.
и образующая трубки. А это противоречит теореме единственности векторных линий.
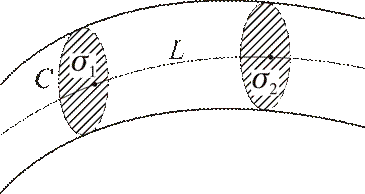
Рис. 9.7
Дивергенция векторного поля.
Определение.
Дивергенцией векторного поля
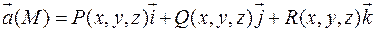
называется функция
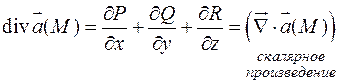
Свойства дивергенции:
1) линейность:
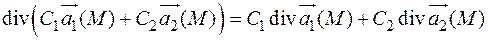
или 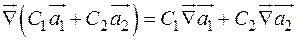
2) если 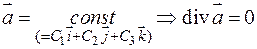
3) если 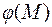 – скалярное поле, то
– скалярное поле, то
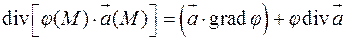
или 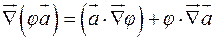
Пример:
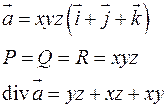
Ротор векторного поля.
Определение.
Роторомвекторного поля 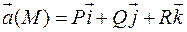 назовем вектор
назовем вектор
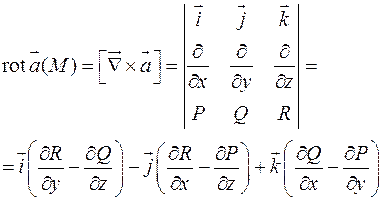
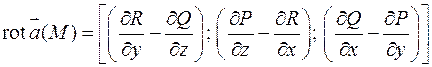
Свойства ротора:
1) 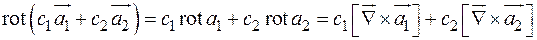 ;
;
2) если 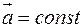 , то
, то  ;
;
3) если  – скалярное поле, то
– скалярное поле, то 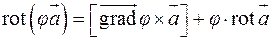
Доказательство:
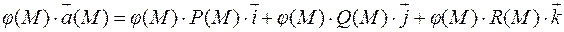
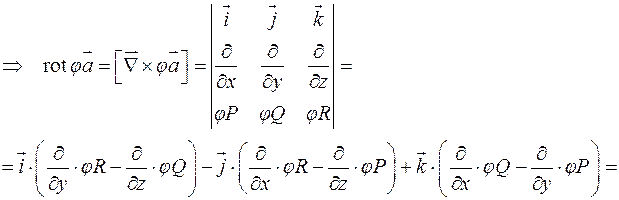
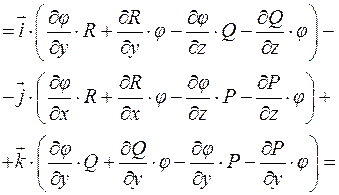
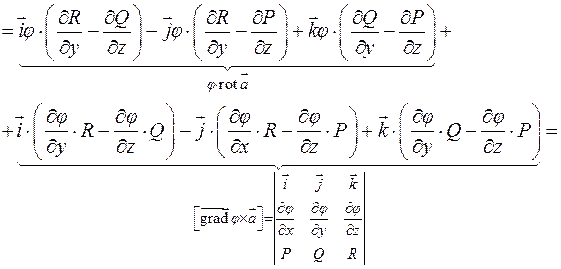
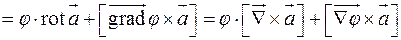

Пример:
Доказать равенство:
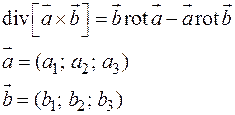
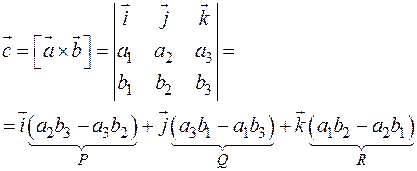
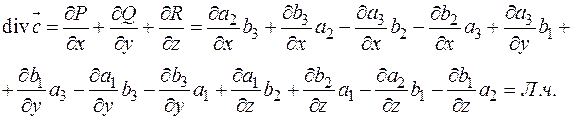
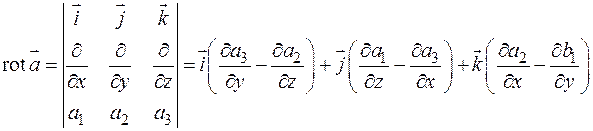
Аналогично выписывается и  . Тогда
. Тогда
П.ч.: 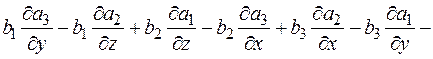
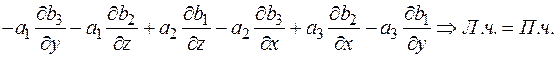
Механический смысл вектора ротора.

Рис. 9.8
Пусть 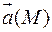 – поле скоростей точек движущегося твердого тела. Следовательно, в любой момент времени t
– поле скоростей точек движущегося твердого тела. Следовательно, в любой момент времени t 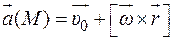 ,
,
где 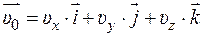 – скорость поступательного движения тела в момент времени t, одинаковая для всех точек тела;
– скорость поступательного движения тела в момент времени t, одинаковая для всех точек тела;
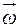 – угловая скорость тела, равная
– угловая скорость тела, равная 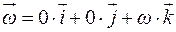 ;
;
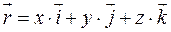 – радиус-вектор точек тела.
– радиус-вектор точек тела.
Если вращение происходит вокруг оси Oz (см. рис. 9.8),то 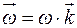 , где
, где 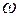 – величина (модуль) угловой скорости и
– величина (модуль) угловой скорости и 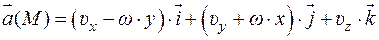 , т.к.
, т.к.
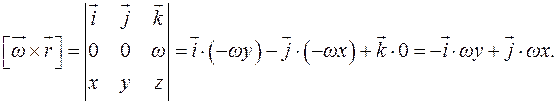
Тогда
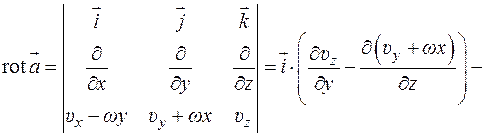
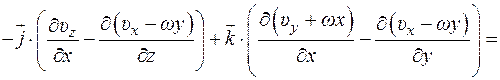
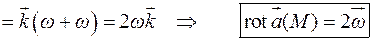
т.е. ротор поля скоростей равен удвоенной угловой скорости твердого тела.
Дифференциальные характеристики 2-го порядка.
Пусть 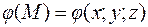 имеет непрерывные частные производные 2-го порядка. Построим функцию
имеет непрерывные частные производные 2-го порядка. Построим функцию  . Оператор
. Оператор 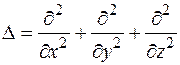 называется дифференциальным оператором Лапласа.
называется дифференциальным оператором Лапласа.
С введенным ранее оператором 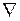 («набла») он связан соотношением:
(«набла») он связан соотношением: 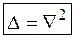 .
.
Действительно, рассмотрим скалярный квадрат
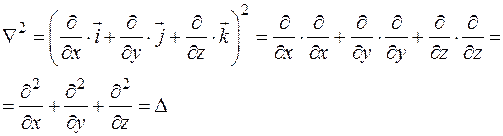
Тогда
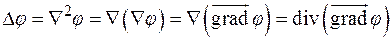
Итак, были введены ранее дифференциальные характеристики 1-го порядка:
1) 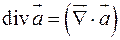 ;
;
2) 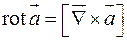 ;
;
3) 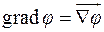
Применяя к полученным полям те же операции (градиент, ротор, дивергенцию), получим дифференциальные характеристики 2-го порядка:
1) 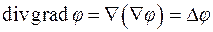 ;
;
2) 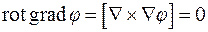 ;
;
3) 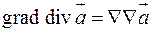 ;
;
4) 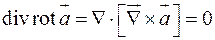 ;
;
5) 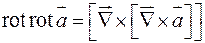
9.5. Поток векторного поля
9.5.1. Поверхностный интеграл II-го рода.
Поверхность  называется двусторонней, если для любой точки М и любого контура С, проходящего через М и не пересекающего границы
называется двусторонней, если для любой точки М и любого контура С, проходящего через М и не пересекающего границы  , после его обхода мы возвратимся в М с исходным направлением нормали. Примеры двусторонней поверхности: сфера, куб, плоскость.
, после его обхода мы возвратимся в М с исходным направлением нормали. Примеры двусторонней поверхности: сфера, куб, плоскость.
Поверхность  – односторонняя, если существует хотя бы один замкнутый контур, обходя который мы вернемся в исходную точку с противоположным направлением нормали.
– односторонняя, если существует хотя бы один замкнутый контур, обходя который мы вернемся в исходную точку с противоположным направлением нормали.
Рассмотрим двустороннюю поверхность  . Выберем одну сторону
. Выберем одну сторону 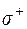 . Пусть функция
. Пусть функция 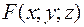 определена в точках этой поверхности, тогда предел
определена в точках этой поверхности, тогда предел
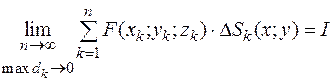 ,
,
где 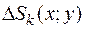 – площадь проекции элемента поверхности
– площадь проекции элемента поверхности  на плоскость хOу, называется поверхностным интегралом II-го рода и обозначается
на плоскость хOу, называется поверхностным интегралом II-го рода и обозначается
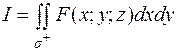
9.5.2. Определение потока векторного поля.
Если 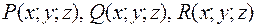 – непрерывны и
– непрерывны и 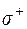 – сторона гладкой поверхности, характеризуемая направлением нормали
– сторона гладкой поверхности, характеризуемая направлением нормали 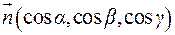 , то поверхностный интеграл II-го рода
, то поверхностный интеграл II-го рода 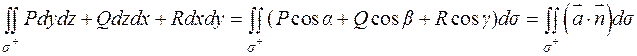 называется потоком векторного поля
называется потоком векторного поля 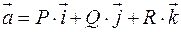 через поверхность
через поверхность  в сторону нормали
в сторону нормали 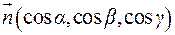 .
.
9.5.3. Физический смысл потока векторного поля.

Рис. 9.9
Пусть векторное поле 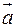 есть поле скоростей стационарного потока несжимаемой жидкости (скорость потока в любой точке постоянна и не зависит от времени). Внутрь потока поместим проницаемую поверхность
есть поле скоростей стационарного потока несжимаемой жидкости (скорость потока в любой точке постоянна и не зависит от времени). Внутрь потока поместим проницаемую поверхность  и определим количество жидкости, протекающей через
и определим количество жидкости, протекающей через  за единицу времени.
за единицу времени.
Рассмотрим вначале случай, когда 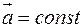 , а площадка
, а площадка 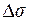 плоская.
плоская.
Тогда количество жидкости равно объему наклонного параллелепипеда с высотой 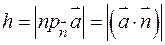 , т.е.
, т.е. 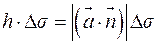 , где
, где 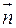 – единичный вектор нормали к
– единичный вектор нормали к  (см. рис. 9.9).
(см. рис. 9.9).
Потоком постоянного векторного поля 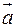 через плоскую площадку
через плоскую площадку 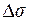 с нормалью
с нормалью 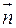 назовем:
назовем:
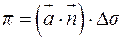 (9.1)
(9.1)
Модуль этой величины равен количеству жидкости, протекающей через 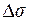 за единицу времени.
за единицу времени.
Рассмотрим теперь произвольное поле 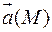 и любую двустороннюю поверхность
и любую двустороннюю поверхность  .
.
Выберем направление нормали к  и разобьем ее произвольно на части
и разобьем ее произвольно на части 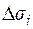 с нормалями
с нормалями 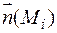 . Считая приближенно площадки
. Считая приближенно площадки 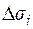 плоскими, а поле в пределах этой малой площадки неизменным, поток через
плоскими, а поле в пределах этой малой площадки неизменным, поток через 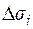 будем считать равным
будем считать равным 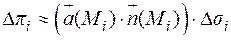 . Тогда поток через всю поверхность
. Тогда поток через всю поверхность  равен:
равен:
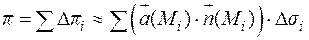 .
.
Переходя к пределу при 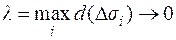 , получим точное значение потока:
, получим точное значение потока:
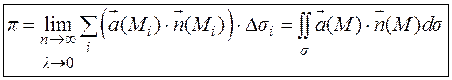 (9.2)
(9.2)
Поток обладает свойствами линейности, аддитивности, при изменении направления нормали к поверхности меняет знак.
9.5.4. Вычисление потока.
Повторим определение потока векторного поля: 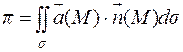
Вычисление потока можно производить методом проектирования поверхности  на какую-либо координатную плоскость. Так, например, если
на какую-либо координатную плоскость. Так, например, если  однозначно проектируется на плоскость хOу, то
однозначно проектируется на плоскость хOу, то 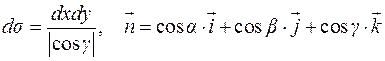 .
.
Если  проектируется на все три координатные плоскости однозначно, то поток можно вычислить по формуле:
проектируется на все три координатные плоскости однозначно, то поток можно вычислить по формуле:
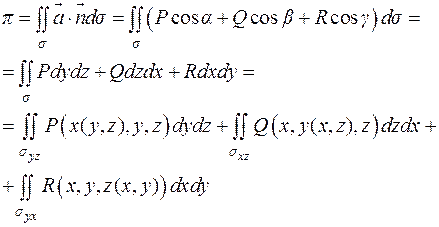
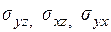 – проекции на соответствующие координатные плоскости.
– проекции на соответствующие координатные плоскости.
Пример:
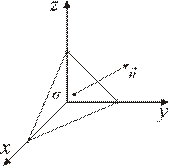
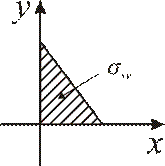
Рис. 9.10
Найти поток векторного поля 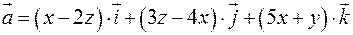 через поверхность треугольника с вершинами в точках
через поверхность треугольника с вершинами в точках 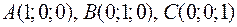 (см. рис. 9.10). Нормаль предполагается направленной от начала координат.
(см. рис. 9.10). Нормаль предполагается направленной от начала координат.
1) Первый способ:
Уравнение плоскости треугольника: 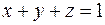 .
.
Нормаль к поверхности, то есть вектор 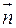 имеет координаты
имеет координаты 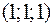 , что следует из уравнения плоскости.
, что следует из уравнения плоскости.
Тогда единичная нормаль:
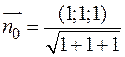 или
или 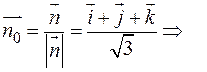
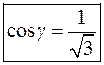
Вычислим скалярное произведение
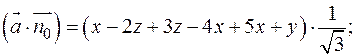
И подставим в формулу для вычисления потока:
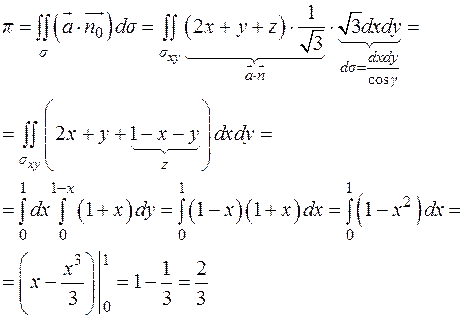
2) Второй способ:
Треугольник ABC однозначно проектируется на все три координатные плоскости.
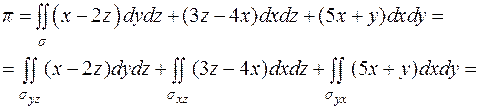
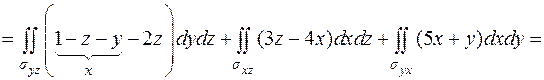
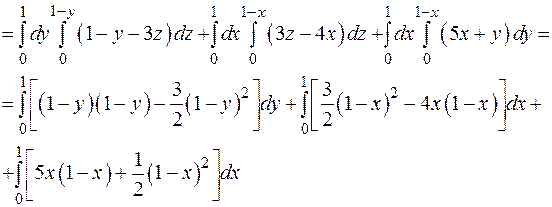
Вычислим три слагаемых отдельно:
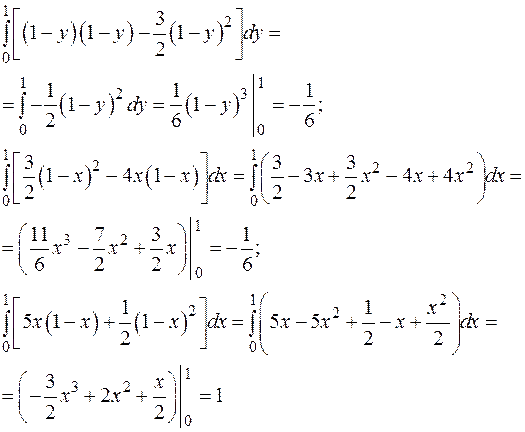
Тогда 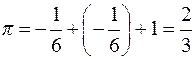
9.5.5. Теорема Остроградского – Гаусса.
Если поверхность  – замкнутая, ограничивающая некоторый объем
– замкнутая, ограничивающая некоторый объем 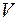 , то поток поля
, то поток поля 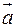 через
через  в направлении внешней нормали равен:
в направлении внешней нормали равен:
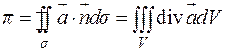 (9.3)
(9.3)
или в координатной форме:
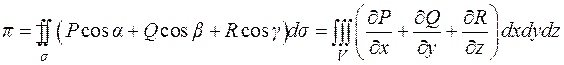
Доказательство:
В начале доказательства приведем следующие соображения. Если объем 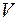 разбить на части
разбить на части 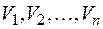 и предположить, что формула (9.3) верна для каждого из объемов
и предположить, что формула (9.3) верна для каждого из объемов 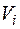 , то она будет верна и для всего объема
, то она будет верна и для всего объема 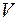 , т.к. для тройного интеграла справедливо свойство аддитивности.
, т.к. для тройного интеграла справедливо свойство аддитивности.
Суммируя поверхностные интегралы по поверхностям 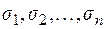 , ограничивающим объемы
, ограничивающим объемы 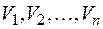 , мы также получим интеграл по поверхности
, мы также получим интеграл по поверхности  , ограничивающей все тело
, ограничивающей все тело 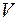 , т.к. интегралы по построенным при разбиении перегородкам внутри
, т.к. интегралы по построенным при разбиении перегородкам внутри  будут браться дважды с противоположными направлениями нормалей и, поэтому, будут взаимно уничтожаться.
будут браться дважды с противоположными направлениями нормалей и, поэтому, будут взаимно уничтожаться.
Разобьем теперь тело 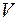 на произвольные части рядом вертикальных поверхностей так, чтобы полученные объемы были просты относительно какой-либо из координатных плоскостей, например, для начала, относительно xOy.
на произвольные части рядом вертикальных поверхностей так, чтобы полученные объемы были просты относительно какой-либо из координатных плоскостей, например, для начала, относительно xOy.
Это означает, что объем 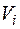 будет ограничен поверхностями
будет ограничен поверхностями 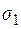 и
и 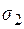 , уравнения которых запишутся соответственно
, уравнения которых запишутся соответственно 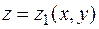 и
и 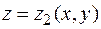 и боковой цилиндрической поверхностью
и боковой цилиндрической поверхностью 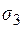 с образующей, параллельной оси Oz (см. рис. 9.11).
с образующей, параллельной оси Oz (см. рис. 9.11).
Поверхности 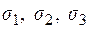 предполагаются кусочно-гладкими. Тело
предполагаются кусочно-гладкими. Тело 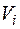 при этом будет проектироваться в область
при этом будет проектироваться в область 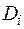 на плоскости xOy.
на плоскости xOy.
Направление нормалей выберем внешними по отношению к объему 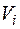 .
.
Обратимся к координатной форме записи теоремы.
Положим  ,
, 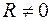 и докажем формулу:
и докажем формулу:
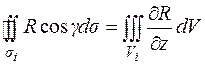 ,
,
где 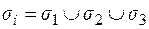 .
.
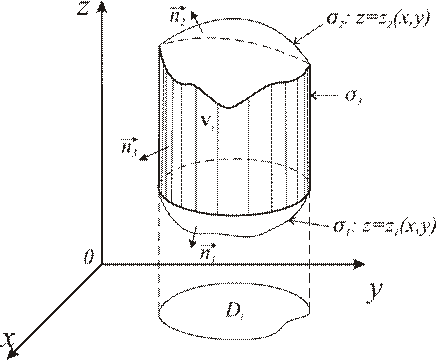
Рис. 9.11
Тройной интеграл в правой части сведем к повторному:
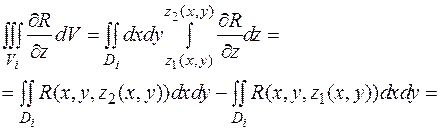
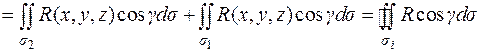 ,
,
т.к. 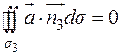 в силу того, что
в силу того, что 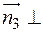 оси Oz, т.е.
оси Oz, т.е. 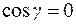 .
.
Аналогичным образом доказываются и две другие части формулы
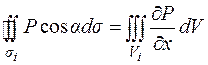
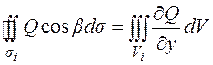 разбиениями
разбиениями 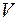 на части
на части 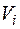 , простые относительно плоскостей yOz и xOz соответственно.
, простые относительно плоскостей yOz и xOz соответственно.
Сложение полученных результатов дает искомую формулу.
Пример:
Вычислить поток векторного поля: 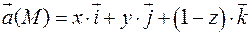 через замкнутую поверхность конуса:
через замкнутую поверхность конуса: 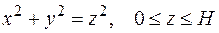 двумя способами: а) непосредственно; б) по теореме Остроградского – Гаусса.
двумя способами: а) непосредственно; б) по теореме Остроградского – Гаусса.
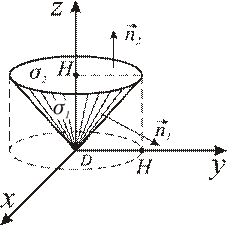
Рис. 9.12
а) непосредственно.
Поверхность состоит из двух частей 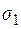 и
и 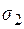 (см. рис. 9.12):
(см. рис. 9.12):
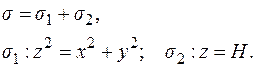
Тогда по свойству аддитивности поток через поверхность  будет являться суммой потоков, протекающих через ее части:
будет являться суммой потоков, протекающих через ее части:
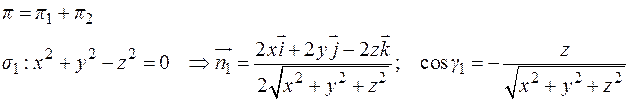
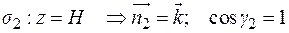
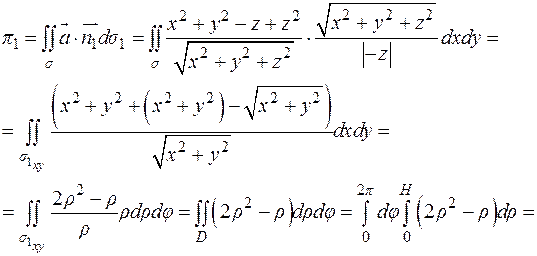
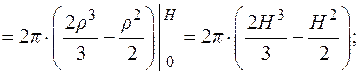
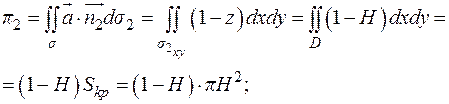
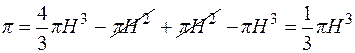 .
.
б) по теореме Остроградского – Гаусса.
Вычислим дивергенцию данного векторного поля:
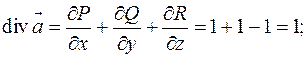
В исследуемой задаче она получилась постоянной, что приводит к удобному вычислению тройного интеграла, как объема конического тела:
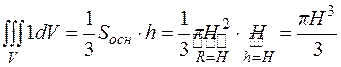
Здесь использовалось свойство тройного интеграла: тройной интеграл от единицы равен объему области интегрирования.
9.5.6. Физический смысл дивергенции. Источники и стоки.

Рис. 9.13
Пусть  – некоторая точка области
– некоторая точка области 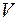 , в которой задано векторное поле
, в которой задано векторное поле 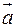 . Окружим
. Окружим 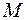 замкнутой поверхностью
замкнутой поверхностью  (см. рис. 9.13), ограничивающей объем
(см. рис. 9.13), ограничивающей объем 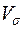 , и применим формулу Гаусса-Остроградского
, и применим формулу Гаусса-Остроградского
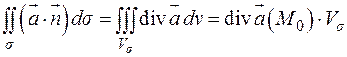
Справа записана теорема о среднем для тройного интеграла. 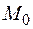 – некоторая «средняя» точка внутри
– некоторая «средняя» точка внутри  . Следовательно,
. Следовательно,
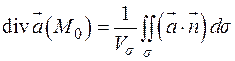 .
.
Перейдем в этом равенстве к пределу, сжимая поверхность  в точку
в точку 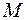 . Тогда
. Тогда 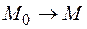 , и в силу непрерывности дивергенции,
, и в силу непрерывности дивергенции, 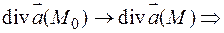
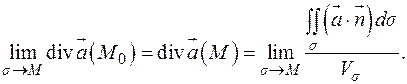
Из этого равенства два вывода:
1. Предел в правой части не зависит от способа стягивания поверхности в точку  , т.к. он равен дивергенции в точке (числу).
, т.к. он равен дивергенции в точке (числу).
2. Так как правая часть определена независимо от выбора систем координат, то инвариантно и понятие дивергенции.
Величина 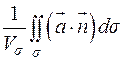 называется средней плотностью потока в окрестности
называется средней плотностью потока в окрестности 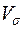 точки
точки 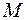 , а ее предел при
, а ее предел при 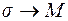 называется плотностью потока в
называется плотностью потока в 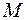
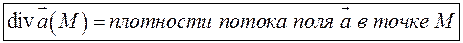
Источники и стоки
Рассмотрим поток векторного поля 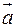 через замкнутую поверхность
через замкнутую поверхность  . Векторное поле будем трактовать как поле скоростей течения жидкости. В этом случае положительное значение потока векторного поля через замкнутую поверхность
. Векторное поле будем трактовать как поле скоростей течения жидкости. В этом случае положительное значение потока векторного поля через замкнутую поверхность  означает, что из области, ограниченной поверхностью
означает, что из области, ограниченной поверхностью  , вытекает жидкости больше, чем втекает в нее. Значит, в области имеются точки или подобласти, в которых жидкость образуется (например, образование воды за счет таяния снега или льда). Точки такого рода называют источниками векторного поля. Аналогично, отрицательное значение потока через поверхность
, вытекает жидкости больше, чем втекает в нее. Значит, в области имеются точки или подобласти, в которых жидкость образуется (например, образование воды за счет таяния снега или льда). Точки такого рода называют источниками векторного поля. Аналогично, отрицательное значение потока через поверхность  означает, что в область втекает жидкости больше, чем вытекает из нее. Значит, в области есть такие точки, в которых жидкость исчезает (например, испаряется или замерзает). Такие точки называются стоками векторного поля.
означает, что в область втекает жидкости больше, чем вытекает из нее. Значит, в области есть такие точки, в которых жидкость исчезает (например, испаряется или замерзает). Такие точки называются стоками векторного поля.
Точечный источник или сток характеризуют интенсивностью, равной объему жидкости, которая возникает или исчезает в этой точке в единицу времени, а распределенные источники или стоки – плотностью интенсивности, т.е. количеством жидкости, возникающей или исчезающей в единице объема в единицу времени. Интенсивность стоков удобно считать отрицательной, полагая, что сток – это источник отрицательной интенсивности. Тогда поток  векторного поля скоростей через поверхность
векторного поля скоростей через поверхность  получает естественную интерпретацию как суммарная интенсивность всех источников и стоков в области, ограниченной этой поверхностью.
получает естественную интерпретацию как суммарная интенсивность всех источников и стоков в области, ограниченной этой поверхностью.
Формула 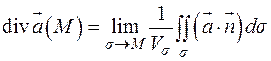 , полученная нами выше, означает, что значение предела определяет интенсивность распределенного источника в точке
, полученная нами выше, означает, что значение предела определяет интенсивность распределенного источника в точке  .
.
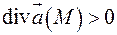 – источник в
– источник в 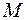 .
.
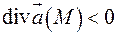 – сток в
– сток в 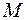 .
.
Т.е. знак дивергенции обозначает преимущество в области источников или стоков.
Символ 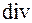 образован от первых букв латинского слова
образован от первых букв латинского слова 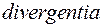 – расхождение. Этот символ, как и само слово «дивергенция», ввел в 1878 г. английский математик Клиффорд. Величину с противоположным знаком Максвелл называл конвергенцией и обозначал
– расхождение. Этот символ, как и само слово «дивергенция», ввел в 1878 г. английский математик Клиффорд. Величину с противоположным знаком Максвелл называл конвергенцией и обозначал 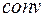 (от латинского
(от латинского 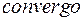 – схожусь).
– схожусь).
9.6. Циркуляция векторного поля
9.6.1. Основные понятия.
Пусть непрерывное векторное поле образовано вектором
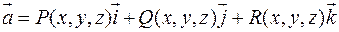
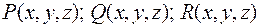 непрерывны, с непрерывными частными производными.
непрерывны, с непрерывными частными производными.
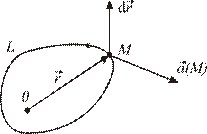
Рис. 9.14
Возьмем в этом поле некоторую кусочно-гладкую замкнутую кривую  и выберем на ней определенное направление (см. рис. 9.14).
и выберем на ней определенное направление (см. рис. 9.14).
Пусть 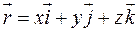 – радиус точки
– радиус точки 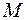 , принадлежащей
, принадлежащей 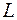 . Вектор
. Вектор 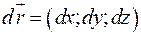 направлен по касательной к
направлен по касательной к 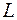 в направлении ее обхода и
в направлении ее обхода и
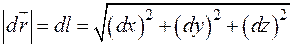 .
.
Циркуляцией вектора 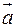 вдоль
вдоль 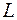 называется интеграл:
называется интеграл:
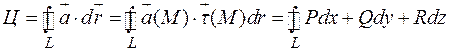 ,
,
т.е. циркуляция – это линейный интеграл векторного поля по замкнутому контуру.
Если рассмотреть векторное поле 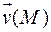 скоростей текущей жидкости и в этот поток поместить замкнутый ко
скоростей текущей жидкости и в этот поток поместить замкнутый ко
Дата добавления: 2020-03-21; просмотров: 629;