Моделирование систем массового обслуживания.
В предыдущем разделе этапы моделирования были рассмотрены на примере такой технической системы, которую можно отнести к системам массового обслуживания (СМО). Такого рода системы очень распространены в современном мире и наиболее часто являются объектами для моделирования, и в связи этим мы рассмотрим довольно подробно теорию массового обслуживания и очередей.
Теория массового обслуживания является одним из разделов прикладной математики (в частности, прикладной математической статистики). Математическим фундаментом теории массового обслуживания являются теория вероятностей и теория случайных процессов. В течение последних десятилетий теория массового обслуживания и теория случайных процессов развивались совершенно синхронно. Наиболее распространенными процессами в СМО являются Марковские процессы и процессы восстановления.
Системы массового обслуживания обычно связаны с очередями, т. е. с цепочками выстроившихся один за другим объектов, нуждающихся в том или ином виде обслуживания. Заявки на обслуживание и есть эти подлежащие обслуживанию объекты, а обслуживающие эти заявки «единицы» - обслуживающие «аппараты». Смысл того, что понимается под заявками на обслуживание и обслуживающим «аппаратом» становится очевиден, если речь идет, например:
а) об обслуживании сервером запросов многих пользователей одного и того же сайта «Интернета»;
б) о попытках дозвониться по телефону, когда набирающие телефонные номера лица обслуживаются в ходе телефонных разговоров;
в) о поступлении на ремонтную базу требующих технического обслуживания транспортных средств, когда в зависимости от численности технического персонала ремонтная база может одновременно обслуживать одно или несколько транспортных средств;
б) о прибытии пациентов на прием к врачу, когда даже при наличии определенной системы предварительной записи по целому ряду причин число ожидающих может флуктуировать и, таким образом, возможно образование очереди;
г) о возникновении очереди у железнодорожной кассы, и т. п.
Как видно уже из приведенных выше примеров, реальные системы по внешней форме и в деталях будут существенно отличаться друг от друга. Однако внутренне они обладают вполне определенными общими чертами. Конкретно, во всех СМО имеют место следующие общие основные элементы:
(а) Входной поток (поток поступающих требований, или заявок на обслуживание). Если акты поступления требований на обслуживание и процедуры обслуживания реализуются строго по графику, то очереди можно избежать. Но на практике всё происходит иначе, и в большинстве случаев поступление требований зависит от внешних обстоятельств. Лучшее, что можно сделать, это описать процесс поступления требований через случайные величины. К числу основных показателей, необходимых для описания входного потока, относятся характеристики источника требований, тип требований и длина интервалов времени между поступлениями требований.
(б) Механизм обслуживания. СМО различаются числом обслуживающих приборов, количеством одновременно обслуживаемых требований, продолжительностью и типом обслуживания. Например, в задачах, возникающих при рассмотрении потоков в сетях (сетевое моделирование) и в задачах составления графиков работы ремонтных предприятий (сетевое планирование) приходится иметь дело с несколькими обслуживающими приборами, функционирующими последовательно и (или) параллельно. Указанные выше характеристики процесса обслуживания также описываются с помощью случайных величин.
(в) Дисциплину очереди. Все другие факторы, относящиеся к правилам поведения очереди, можно включить в этот пункт. К их числу относятся, прежде всего, правила, в соответствии с которыми обслуживающий механизм принимает поступившую заявку к обслуживанию. Такие правила, как «первым пришел — первым обслуживаешься» (сокращенно ПЕРППО), «последним пришел — первым обслуживаешься» (сокр. ПОСППО) и «случайный отбор заявок» (СОЗ), однозначно расшифровываются своими названиями.
Во многих ситуациях с целью придания описанию исследуемого процесса большего реализма приходится прибегать к понятию «приоритет». Ряд других факторов, которые также можно отнести к данному пункту, отражают особенности индивидуального поведения клиентов (уклонение от обслуживания, переход из одной очереди в другую, обманные действия клиентов и т. п.).
В теории массового обслуживания рассматриваются системы, обладающие указанными выше характеристиками. Эта теория вооружает нас методологией и способами формализованного описания таких систем. При теоретическом рассмотрении СМО выявляется связь теории СМО с другими разделами дискретной математики, такими, как Марковские процессы, временные ряды, статистический анализ случайных процессов и т. д.
Всякая СМО характеризуется следующими тремя элементами:
1) Вид входного потока;
2) Распределение продолжительности обслуживания;
3) Число обслуживающих приборов.
Различные распределения обозначаются буквами. Обычно используются следующие буквенные обозначения: М — пуассоновское распределение потока заявок (М отражает тот факт, что процесс обладает марковским свойством), D — постоянная величина, Еk — распределение Эрланга (гамма-распределение с целочисленным параметром k), G — произвольное распределение и GI — распределение в случае независимых (рекуррентных) событий.
Таким образом, в этих обозначениях под системой типа М/D/s понимается система с s приборами, обслуживающими поступающие требования за строго определенное время, причем интервалы времени между последовательными поступлениями заявок распределены по закону Пуассона, иначе говоря, входной поток заявок является пуассоновским, т.е. потоком стационарным, ординарным и без последействия. В теории массового обслуживания пуассоновское распределение занимает особое место. Впервые оно было получено Пуассоном и рассмотрено в его трактате по теории вероятностей, изданном в 1837 г. Важность этого распределения для моделирования систем телефонной связи была установлена Эрлангом в 1948 г. в его основополагающей работе.
К числу основных операционных характеристик любой СМО относятся:
L(t) — длина очереди в момент времени t , или число требований, находящихся в системе в момент времени t ;
Ln — длина очереди на n-й стадии. Предполагается, что стадии реализуются в дискретном режиме и определяются теми или иными событиями (например, поступлением требования в систему или выбытием требования из системы);
T(t) — продолжительность ожидания относительно момента времени t , т.е. время ожидания обслуживания требования, которое поступит в систему в момент времени t;
Tn — продолжительность периода, в течение которого n-е требование ожидает обслуживания;
Ti — продолжительность периода занятости системы, начало которого соответствует L(0) = i , т. е. длина периода занятости системы, начинающегося при наличии в системе i требований (при i = 1, так же как и при i = 0 в момент, непосредственно предшествующий поступлению требования на обслуживание, систему принято считать начавшей функционировать, т. е. занятой);
I(n) — продолжительность n-го периода простоя системы, т. е. длина интервала времени, в течение которого система в n-й раз оказывается незанятой (в системах обслуживания периоды простоя сменяются периодами занятости).
Наряду с указанными операционными характеристиками в теории массового обслуживания используются их различные модификации, такие, как полная продолжительность пребывания требования в системе, операционный цикл (сумма продолжительностей периода занятости и непосредственно следующего за ним периода простоя), суммарное полезное время (доля времени, в течение которого обслуживающий механизм находится в состоянии загруженности).
Поскольку процесс поступления требований и (или) процесс обслуживания носят случайный характер, то распределения представляют собой случайные процессы в соответствующих пространствах состояний и параметров, а являются случайными величинами. Определение свойств распределений и моментов L(t) , Ln , T(t) , Tn , Ti , I(n) и есть та основная цель, которая преследуется при моделировании и анализе поведения СМО.
Длина очереди не зависит от дисциплины очереди при условии, что: а) до тех пор, пока в системе имеются неудовлетворенные требования, обслуживающий механизм не прекращает функционировать, б) обслуживание любого требования доводится до конца и в) дисциплина очереди не основана на приоритете динамического типа. В том случае, когда имеет место дисциплина типа ПЕРППО и система располагает лишь одним обслуживающим прибором, виртуальная продолжительность ожидания фактически совпадает с длительностью периода загрузки обслуживающего прибора.
Многие СМО обладают тем свойством, что по истечении определенного времени их поведение в некотором смысле стабилизируется. Формально это выражается в появлении определенных свойств процессов { L(t) } , { T(t) }, при t ®- ¥ и { Ln } и { Tn } при n ® ¥. Для удобства используют следующими обозначениями: L(¥) = L ; T (¥) = T , Ln®¥ = L¥ и Tn®¥ = T¥ . Когда поведение системы полностью стабилизируется (т. е. перестает меняться с течением времени), говорят, что процесс ее функционирования является стационарным, или равновесным. Условия, при которых системы переходят в стационарное состояние, представляют особый интерес.
На практике удобнее оперировать простыми и легко измеримыми показателями, нежели сложными формулами для распределений вероятностей и моментов. Выбор показателей такого рода, разумеется, зависит от характера исследуемой системы и целей анализа. Наиболее часто используемым показателем является степень загруженности обслуживающего прибора, определяемая коэффициентом нагрузки системы a =l/m . Здесь l - интенсивность поступления требований (количество требований, поступающих в систему в единицу времени) , а m - интенсивность обслуживания (число требований, обслуживаемых в единицу времени). Коэффициент нагрузки a , определяющий долю времени, в течение которого обслуживающий прибор оказывается загруженным, принят в качестве международной единицы измерения, которую назвали эрлангом (как признание большого вклада, который внес Эрланг в теорию телефонной связи).
Области приложений теории массового обслуживания весьма разнообразны. К их числу относятся сети типа Интернет, транспортные системы, электронно-вычислительные комплексы, система медицинского и бытового обслуживания и т. п. В каждой из них возникают задачи разных типов и разные подходы к их решению. Классификация целевых назначений теории массового обслуживания основана на выделении в ее структуре различных классов задач и соответственно областей применения получаемых результатов. Можно выделить следующие классы задач:
(а)Задачи анализа поведения системы, или системный анализ СМО.
(б) Статистические задачи, или задачи статистического моделирования СМО.
(в) Операционные задачи, или задачи исследования операций в СМО.
Цель рассмотрения задач такого рода заключается в том, чтобы с помощью математических моделей, более или менее детально отражающих свойства реальных СМО, выявить операционные характеристики, определяющие поведение этих систем в процессе их функционирования.
Системы массового обслуживания широко распространены в современном мире. Это аэродромы, радиолокационные станции, технологические линии АТС и т.п. Работа любой СМО заключается в обслуживании заявок, поступающих на нее потоком. Заявки поступают в общем случае в произвольные моменты времени. Обслуживание поступившей заявки продолжается в течение времени обслуживания Тобс после чего СМО освобождается и готова к приему следующей заявки. Каждая СМО может состоять из одного или нескольких каналов обслуживания. Работа некоторой гипотетической СМО схематически представлена на рисунке ниже.
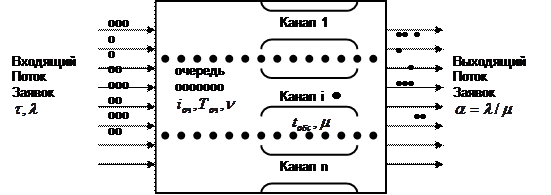 |
Рис. 7. Схема работы системы массового обслуживания
Входящий поток заявок характеризуется средним временем между заявками, плотностью потока заявок 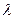 = l/τ. Каждый канал характеризуется средним временем обслуживания tобс и пропускной способностью канала μ = 1/tобс. Кроме среднего времени обслуживания, важен также закон распределения времени обслуживания P = P(tобс<t), который чаще всего оказывается показательным Р = 1-
= l/τ. Каждый канал характеризуется средним временем обслуживания tобс и пропускной способностью канала μ = 1/tобс. Кроме среднего времени обслуживания, важен также закон распределения времени обслуживания P = P(tобс<t), который чаще всего оказывается показательным Р = 1- 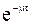 . Выходящий поток заявок характеризуется интенсивностью
. Выходящий поток заявок характеризуется интенсивностью 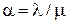 .
.
Если 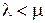 для одного канала, то канал не справляется с потоком заявок и возникает очередь длиной lоч со средним временем нахождения в очереди Точ и темпом прироста очереди ν.
для одного канала, то канал не справляется с потоком заявок и возникает очередь длиной lоч со средним временем нахождения в очереди Точ и темпом прироста очереди ν.
На практике чаще всего встречаются простейшие потоки, т.е. потоки стационарные, ординарные и без последействия. Поток называется стационарным если плотность потока λ не зависит от времени. Примером стационарного потока является течение реки без учета сезонных колебаний уровня и т.п. Условие ординарности означает, что заявки поступают в СМО поодиночке, а не парами, тройками и т.д. Примером ординарного потока является поток снарядов по цепи, если только стрельба не ведется залпами.
Поток считается без последействия, если для любых неперекрывающихся интервалов времени число событий, попадающих на один из интервалов, не зависит от числа событий, попадающих на другие интервалы. Например, последействие отсутствует для потока пассажиров, подходящих к остановке, но для пассажиров, отходящих от остановки, оно имеется, поскольку их движение скоррелировано движением транспорта. Прореживая простейший поток, можно получить так называемые потоки Эрланга. Так, если исключить из потока заявок каждую вторую, то получим поток Эрланга 1-го порядка. Если оставить в потоке каждую третью заявку, то будем иметь поток Эрланга 2-го порядка и т.д. Для простейшего потока вероятность поступления заявки имеет показательный закон распределения Р = 1- 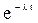 .
.
Если СМО не в состоянии обслужить все поступающие заявки, то возникает система с отказами либо система с ожиданием (очередь). Примером СМО с отказами является телефонная линия, которая, будучи занятой, отменяет заявки абонента. В системе, где очередь допускается, возможны ограничения на длину очереди, время ожидания в очереди либо общее время пребывания заявки в системе.
Критерием эффективности СМО с отказами является вероятность отказа в обслуживании. Степень загрузки СМО с отказами характеризуется законом распределения числа занятых каналов либо просто средним числом занятых каналов.
Работающая n-канальная СМО может быть представлена в виде физической системы, находящейся в каком-либо из состояний:
s0 - свободны все каналы;
s1 - занят один канал, остальные свободны;
s2 - занято два канала, остальные свободны;
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
sn - заняты все n каналов.
При наличии простейшего , т.е. для показательного закона распределения заявок λ потока заявок плотности по времени вероятности Рk нахождения СМО в состояниях sk(k=0,1,2,...,n) определяются формулами Эрланга, которые оказываются справедливыми и для произвольного закона обслуживания.
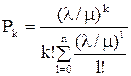 ,
,
где μ - пропускная способность каждого канала, а время обслуживания также имеет произвольный закон распределения.
Для СМО с отказами вероятность отказа Ротк=Р совпадает с вероятностью занятия всех n каналов. Среднее число занятых каналов 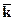 просто связано с вероятностью отказа:
просто связано с вероятностью отказа:
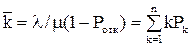 .
.
При наличии СМО с ожиданием, кроме перечисленных состояний системы, возможны следующие:
sn - заняты n каналов, очереди нет;
sn+1 - заняты n каналов, одна заявка в очереди;
sn+2 – заняты n каналов, две заявки в очереди;
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼;
sn+m – заняты n каналов m заявок в очереди.
Время ожидания в очереди Точ, как и время обслуживания, чаще всего распределено по показательному закону Р(Точ<t)=l-e-vt, где v - величина, обратная среднему времени ожидания.
Для так называемой чистой системы с ожиданием (ν=0) имеется формула для расчета среднего числа 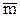 заявок в очереди:
заявок в очереди:
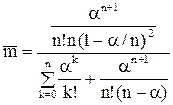 ;
; 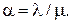 .
.
Среднее время ожидания заявки в очереди 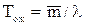 . Возможна также система смешанного типа с ограничением на длину очереди, в которой заявка становится в очередь, если ее длина не превышает некоторого значения q. Для такой СМО вероятность отказа, т.е. вероятность предельного состояния sn+q, определяется формулой:
. Возможна также система смешанного типа с ограничением на длину очереди, в которой заявка становится в очередь, если ее длина не превышает некоторого значения q. Для такой СМО вероятность отказа, т.е. вероятность предельного состояния sn+q, определяется формулой:
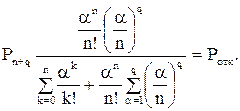 .
.
Среднее число заявок 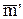 в очереди не превышает q и определяется формулой
в очереди не превышает q и определяется формулой
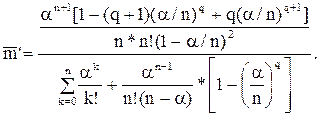 .
.
Среднее время ожидания и для "чистой системы с ожиданием", и для очереди с ограничением одинаково и равно 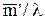 .
.
Дата добавления: 2022-07-20; просмотров: 83;










