Числа фиббоначчи – фиббоначчи саннары
Задано следующее рекурентное соотношение:
F0=1, F1=1, Fi= Fi-1+Fi-2, т.е. 1, 1, 2, 3, 5, 8, 13, 21, 34…
Для решения этой задачи можно использовать рекурсивную функцию:
Function fibbonachi(n:integer):integer;
Begin
If n=0 then fibbonachi:=1
Else
If n=1 then fibbonachi:=1
Else
fibbonachi:=fibbonachi(n-1)+ fibbonachi(n-2)
End;
Либо итеративную функцию:
Function fibbonachi(n:integer):integer;
Var f,f1,f2,I:integer;
Begin
If n=0 then fibbonachi:=1
Else
If n=1 then fibbonachi:=1
Else
begin
f1:=1;
f2:=1;
for I:=2 to n do
begin
f:=f1+f2;
f2:=f1;
f1:=f
end;
fibbonachi:=f
end
End;
Рассмотрим еще две задачи на рекурсию.
1) Задана лестница с n ступенями. При подъеме по лестнице можно шагать либо на следующую ступень, либо через одну ступень, либо через две. Нужно определить сколькими различными способами можно подняться по данной лестнице.
Решение
При n=1 – 1.
При n=2 – 2 (1+1, 2).
При n=3 – 4 (1+1+1, 1+2, 2+1, 3).
Далее число вариантов зависит от предыдуших ступеней, т.е. F(n)= F(n-1) + F(n-2) + F(n-3).
Для решения этой задачи можно использовать рекурсивную функцию:
def baskch(n) :
if n==1 : return 1
if n==2 : return 2
if n==3 : return 4
return baskch(n-1)+ baskch(n-2) + baskch(n-3)
Либо итерративную функцию:
def baskch(n) :
if n==1 : return 1
if n==2 : return 2
if n==3 : return 4
return baskch(n-1)+ baskch(n-2) + baskch(n-3)
f1=1
f2=2
f3=4
for i in range(n-2) :
f:=f1+f2+f3
f3:=f2
f2:=f1
f1:=f
return f
2) Задан круг с 2k вершинами на ней. Пары вершин соединяются хордами, не имеющими общих концов. Определить число различных вариантов соединений вершин хордами, дающих минимальное разбиение круга своими сечениями.
Решение.
Если задана какая-то разбивка круга хордами и очередная хорда не пересекает остальные хорды, то число областей увеличится на 1. Если же данная хорда будет пересекать при соединении вершин другие хорды, то число областей увеличится больше чем на 1. Отсюда следует, что в минимальном разбиении хорды не должны пересекаться и число областей образованных хордами будет равняться k+1.
При k=0 число вариантов F(0)=1.
При k=1 число вариантов F(1)=1.
При k=2 число вариантов F(2)=2.
2 2
1 3
1 3
4 4
Для решения задачи перенумируем вершины по часовой стрелке.
В этом случае число вариантов определяется разбиением всех хорд круга, первой исходящей хордой из вершины 1. Она может присоединятся только к вершинам с четными номерами, иначе будут пересечения хорд и число областей не будет минимальной. Тогда число вариантов разбиения F(2)=F’(2-число вершин между 1 и 4 по часовой стрелке по кругу, 0 - число вершин между 4 и 1 по часовой стрелке по кругу)+F’(0,2)=F(1)*F(0)+ F(0)*F(1)=1*1+1*1=2.
Для произвольного k при переборе вариантов проведения хорд из вершины 1 будет следующая формула:
F(k)= F(0)*F(k-1)+F(1)*F(k-2)+F(2)*F(k-3)+…+F(k-2)*F(1)+ F(k-1)*F(0)
В зависимости от значения k для вектора F нужно подобрать соответствующий тип. В случае необходимости при больших значениях k необходимо будет представить их в виде векторов разряда числа и соответственно написать процедуры вычисления арифметических операций над ними.
Для ускорения вычисления чисел Фибоначчи можно обратиться к использованию матриц следующего вида
| А | ||
Если мы рассмотрим степени этой матрицы
| А1= | А2= | А3= | …Аi= | Fi+1 | Fi | ||||||
| Fi | Fi-1 |
То обнаружим, что значения элементов степеней этой матрицы совпадают с числами Фибоначчи данного порядка.
Обнаружив это свойство матрицы, можно использовать математический аппарат матриц. Используя свойства матриц можно ускорить вычисления чисел фиббоначчи. Для этого рассмотрим умножение матриц
| А*В = | A11 | A12 | * | B11 | B12 | = | A11B11+A12 B21 | A11B12+A12 B22 |
| A21 | A22 | B21 | B22 | A21B11+A22 B21 | A21B12+A22 B22 |
Процесс вычисления произведения таких матриц требует выполнения 12 арифметических операций. Если процесс вычисления матрицы будет производится в соответствии с определением Аn=АAA…A, то арифметических операций потребуется 12(n-1). И для вычисления чисел Фибоначчи при малых n с использованием матриц требует большего времени.
Для решения этой задачи при больших n далее рассмотрим степени матрицы А.
А1, А2(12), А3=AAA=А2А(24), А4=АAAA(36)=А3A(36)=(А2)2(24)…
А8=АAAAАAAA(86)=…= (((А2)2) 2(36)…
Т.е. степени матрицы могут быть получены разными способами: либо через произведение всех матриц, определяющих ее степень, либо с использованием промежуточных вычислений можно сократить процесс вычисления степени матрицы.
Например при
n=2k=32, Аn=((((A2)2)2)2)2 - требуется 60 арифметических операций;
n=73=64+8+1=1*20+0*21+0*22+1*23+0*24+0*25+1*22
A A2 A4 A8 A16 A32 A64
Аn= А73= A * A8 * A64
Таким образом, видно, что для данного случая вычислений с помощью матриц требуется 8*12=96 арифметических операций вместо 73*12=876;
3. n=2k=256, Аn=(((((((A2)2)2)2)2)2)2)2 — требуется 8*12=96 арифметических операций с помощью матрицы вместо 255 операций при обычным способе.
Число арифметических операций для вычисления чисел Фибоначчи при быстром умножении матриц равно сумме числа единиц в двоичном разложении n и числу значащих разрядов n, умноженной на 12. Это число колеблется от 12 ∟log2 n до 24 ∟log2 n [7]. Программа имеет следующий вид:
Program Fibbonachi;
Type tabn=array[1..2,1..2] of long int
Var A,B:tabn;
I,j,k,n:integer;
Procedure tapkrlau(a,b: tabn; var c: tabn);
Begin
C[1,1]:=B[1,1]*A[1,1]+ B[1,2]*A[2,1];
C[1,2]:=B[1,1]*A[1,2]+ B[1,2]*A[2,2];
C[2,1]:=B[2,1]*A[1,1]+ B[2,2]*A[2,1];
C[2,2]:=B[2,1]*A[1,2]+ B[2,2]*A[2,2];
End;
Begin
Read(n);
A[1,1]:=1; A[1,2]:=1; A[2,1]:=1; A[2,2]:=0;
B[1,1]:=1; B[1,2]:=0; Bb[2,1]:=0; B[2,2]:=1; {A0}
While n<>0 do
If n mod 2=1 then
Tapkrlau(B,A,B);
Tapkrlau(A,A,A);
n:=n div 2
End;
Write(B[1,2])
End.
Теория графов
Граф G(X,A) – это совокупность элементов X={x1, x2, x3, … xn,} с его множеством связей A={<xi1, xj1>, <xi2, xj2>,<xi3, xj3>, … <xik, xjk>} где n – число вершин, k – число связей.
X={1,2,3,4,5,6}
A={<1,2>,<1,3>,<1,4>,<5,4>,<2,5>,<6,2>,<5,6>,<6,5>,<6,3>}
Граф G(X,A) – называется неориентированным графом, если в А для любой связи <xi,xj> существует связь <xj, xi>.
Графы могут иметь различное представление:
· Графическое
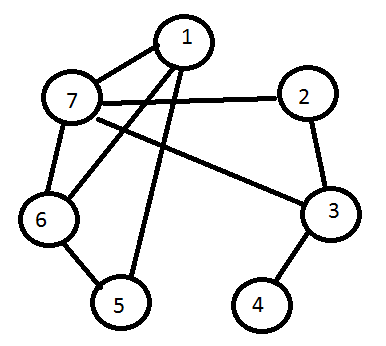
· список элементов связи
A={<1,5>,<1,6>,<1,7>,<2,7>,<3,7>,<2,3>,<3,4>,<5,6>,<6,7>}
· матрица смежности
| , где Ai,j принимает значение 1 при наличии связи из i в j, иначе 0. | ||||||||
| A= | ||||||||
Неориентированные графы имеют симметричную матрицу смежности и его связи называются ребрами, а для ориентированных графов связи называются дугами.
· Матрица инцеденций
| , где строки соответствуют ребрам, а столбцы вершинам. Для i –го ребра <j,k> в строке i Ai,j=1 Ai,k=1 | ||||||||
| A= | ||||||||
имеющий размер m x n.
Рассмотрим программу преобразования графа из формы списка элементов связи в остальные формы и проверкуналичия эйлерова цикла в графе с помощью матрицы смежности.
Program convert;
Const n=7;
Var a_insedent:array[1..m,1..n] of integer;{ матрица инциденций }
A_smegn:array[1..n,1..n]of integer;{матрица смежности }
A_spisok:array[1..2,n*(n-1)] of integer;{ список элементов связей-ребер}
I,j,m,chэslo_reber:integer;
Svazanoe_mnogestvo:set of 1..n;{связаное множество для решения задачи об эйлеровом цикле }
Proverochnij_vector:array[1..n] of integer;
Ejler:Boolean;
Begin
{инициализация массивов}
For i:=1 to n do Begin
For j:=1 to n do A_smegn[i,j]:=0;
For j:=1 to m do A_insedent[j,i]:=0
End;
For i:=1 to n*(n-1) do begin A_spisok[1,i]:=0; A_spisok[2,i]:=0 end;
{Ввод списка связей }
m:=0;
while not eof do
begin
m+=1;
readln(A_spisok[1,m],A_spisok[2,m]);
{формирование матрицы смежности}
A_smegn[A_spisok[1,m],A_spisok[2,m]]:=1;
A_smegn[A_spisok[2,m],A_spisok[1,m]]:=1;
{формирование матрицы инцеденций}
A_insedent[m,A_spisok[1,m]]:=1;
A_insedent[m,A_spisok[2,m]]:=1;
end;
{Проверка наличия эйлерова цикла в графе разлагается на две задачи:
— проверка связанности графа, т.е. наличия соединяющих путей (последовательности ребер с общими концами) для любой пары вершин;
— наличия замкнутого пути, проходящего по всем ребрам, который определяется четносьтю степеней всех вершин в графе}
ejler:=true;{проверяется нарушение свойства эйлерова цикла}
Svazanoe_mnogestvo:=[1];
Proverochnij_vector[1]:=1;
i:=1;{номер проверяемой вершины в Proverochnij_vector }
J:=2;{ свободное место в Proverochnij_vector }
Whэle i<>j do {пока компанента связанности не проверена выполнить}
Begin
Chэslo_reber:=0;
For m:=1 to n do
If A_smegn[m,Proverochnij_vector[I]=1 then
Begin
Chislo_reber:=Chislo_reber+1;
If not(m in Svazanoe_mnogestvo) then
begin
Proverochnij_vector[j]:=m;
Svazanoe_mnogestvo:= Svazanoe_mnogestvo+[m]
end
End;
If odd Chislo_reber then ejler:=false
i+=1;
End;
If Svazanoe_mnogestvo<>[1..n] then ejler:=false;
if ejler then write(‘эйлеров цикл есть’)
Else write(‘эйлерова цикл нет’)
End.
Перебор подмножест
Пусть задано множество X={x1, x2, x3}. Переберем все подмножества – Бирелгән төркемне аралап чыгыйк
x1, x2, x3
0 0 0 - > { }
0 0 1 - > {x1 }
0 1 0 - > { x2 }
0 1 1 - > {x1, x2 }
1 0 0 - > { x3}
1 0 1 - > {x1, x3}
1 1 0 - > { x2, x3}
1 1 1 - > {x1, x2, x3}
Следующая программа проводит этот перебор как перебор двоичного кода в векторе с n разрядами
uses crt;
const
n=4;
k=12;
var
mn,p:array[1..n] of integer;
i,y:integer;
bette:boolean;
begin
clrscr;
write('(');
for i:=1 to n do
begin
mn[i]:=0;
write(' 0');
p[i]:=random(9)+1;
end;
writeln(' ) -> {} = 0');
repeat
{добавить 1 }
y:=0;
i:=n;
while mn[i]=1 do
begin
mn[i]:=0;
i:=i-1
end;
mn[i]:=1;
for i:=1 to n do
if mn[i]=1 then y:=y+p[i];
{печать множества }
write('(');
for i:=1 to n do
write(mn[i]:2);
write(' ) -> {');
for i:=n downto 1 do
if mn[n-i+1]=1 then
write(' X',i);
writeln('} =',y);
{проверка конца }
bette:=true;
for i:=1 to n do
if mn[i]=0 then
bette:=false
until bette
end.
Дата добавления: 2022-04-12; просмотров: 236;











