Постановка задач линейного программирования
Промышленное производство, ресурсы в экономике, напряжение сил в военных действиях – это комплексы многочисленных взаимоувязанных процессов. В управлении этими совершенно различными явлениями можно выделить существенные черты сходства. При описании задач оптимизации оказывается, что задачи, различные по содержанию, могут быть представлены однотипными математическими моделями.
Наиболее простой и изученной является модель линейного программирования. Она содержит в себе три основных момента:
§ набор неотрицательных переменных, характеризующих изучаемый процесс или явление;
§ соотношения, устанавливающие связь между переменными (ограничения) и отражающие требования задачи;
§ критерий оптимальности (функцию цели).
В задачах линейного программирования ограничения представляют собой систему линейных неравенств и уравнений, выражающих условие материального баланса (т.е. чтобы расход любого вида сырья не превышал имеющегося запаса данного сырья и т.д.). Функция цели тоже имеет линейный вид.
Прежде чем перейти к рассмотрению общей задачи линейного программирования, разберем несколько примеров.
Задача производственного планирования.Предположим, что на некотором предприятии имеется 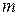 видов сырья для производства
видов сырья для производства 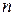 видов изделий. Известны нормы расхода каждого вида сырья на единицу каждого вида изделия. Кроме того, известны запасы каждого вида сырья и доход предприятия от реализации единицы изделий каждого вида.
видов изделий. Известны нормы расхода каждого вида сырья на единицу каждого вида изделия. Кроме того, известны запасы каждого вида сырья и доход предприятия от реализации единицы изделий каждого вида.
Задача производственного планирования состоит в определении количества изделий каждого вида, которое должно производить предприятие, чтобы расход имеющегося сырья не превышал его запасы, а доход предприятия был бы как можно больше, т.е. достигал максимума.
Примем следующие обозначения:
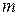 – –
| число ресурсов (число видов сырья); |
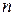 – –
| число видов изделий; |
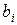 – –
| запасы сырья 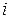 -го вида -го вида 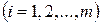 ; ;
|
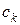 – –
| доход от продажи 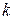 -го изделия -го изделия 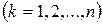 ; ;
|
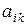 – –
| норма расхода сырья 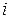 -го вида на производство одного изделия -го вида на производство одного изделия 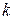 -го вида -го вида 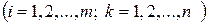
|
Очень удобной формой записи условия задачи является таблица следующего вида.
Таблица 1
| Виды сырья | Норма расхода 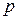 -го сырья на -го сырья на 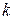 -ое изделий -ое изделий
| Запасы сырья | ||||
| В и д ы и з д е л и й | ||||||
| 1 | 2 | 3 | … | 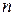
| ||
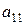
| 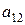
| 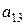
| … | 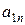
| 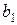
| |
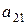
| 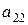
| 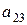
| … | 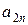
| 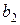
| |
| … | … | … | … | … | … | … |
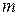
| 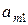
| 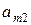
| 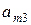
| … | 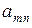
| 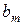
|
| Доход | 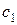
| 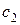
| 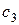
| … | 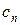
| 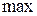
|
В качестве неизвестных в задачах линейного программирования берут те величины, которые нужно определить. В данной задаче:
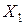 – –
| количество изделий 1-го вида, которое должно произвести предприятие; |
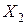 – –
| количество изделий 2-го вида; |
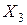 – –
| количество изделий 3-го вида; |
| ……………………………………… | |
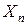 – –
| количество изделий 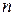 -го вида. -го вида.
|
Составим ограничения.
Если на одно изделие I вида расходуется 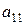 первого вида сырья, то на все изделия I вида сырья пойдет
первого вида сырья, то на все изделия I вида сырья пойдет 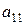
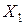 . На все изделия II вида этого же сырья потребуется
. На все изделия II вида этого же сырья потребуется 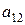
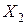 (так как на одно изделие идет
(так как на одно изделие идет 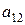 , а всего изделий
, а всего изделий 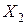 ). На все изделия III вида необходимо
). На все изделия III вида необходимо 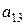
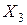 сырья I вида и т.д., и, наконец, для производства последнего вида изделий сырья I вида потребуется
сырья I вида и т.д., и, наконец, для производства последнего вида изделий сырья I вида потребуется 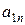
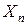 . Всего сырья I вида будет израсходовано:
. Всего сырья I вида будет израсходовано:
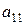
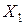 +
+ 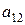
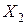 +
+ 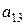
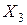 + … +
+ … + 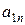
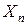
– эта величина складывается из расходов сырья I вида по каждому виду изделия. А так как запасы ограничены, то эта сумма не должна превышать величину запаса по этому виду сырья (т.е. должна быть меньше ее или равна ей):
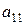
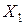 +
+ 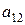
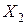 + … +
+ … + 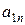
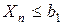 .
.
Аналогично по второму виду сырья: следует учесть расходы этого сырья по всем изделиям каждого вида, а затем найти суммарный расход, и этот расход сырья II вида не должен превосходить запасы сырья этого вида. Тем самым получим второе ограничение
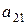
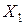 +
+ 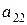
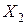 + … +
+ … + 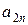
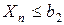 .
.
Проведя подобные рассуждения для всех видов сырья, получим систему ограничений, описывающую данную задачу:
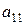
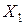 +
+ 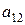
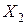 + … +
+ … + 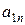
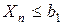 ,
,
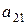
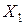 +
+ 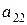
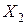 + … +
+ … + 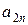
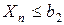 ,
,
……………………………………..
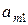
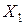 +
+ 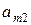
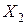 + … +
+ … + 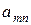
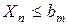 .
.
Поскольку количество изделий любого вида не может быть отрицательным, требуем, чтобы все введенные неизвестные были больше нуля или, в крайнем случае, равны нулю.
Доход, получаемый от производства всех изделий первого вида, составляет 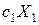 ; от производства изделий второго вида –
; от производства изделий второго вида – 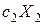 и т.д. и от производства изделий
и т.д. и от производства изделий 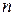 -го вида он равен
-го вида он равен 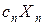 . Общий доход выразится в виде суммы этих величин.
. Общий доход выразится в виде суммы этих величин.
Таким образом, задача заключается в нахождении таких переменных 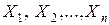 , которые удовлетворяют условиям
, которые удовлетворяют условиям
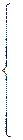
| 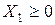 , , 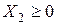 , … , , … , 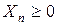
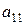 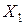 + + 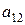 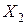 + … + + … + 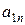 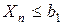 , ,
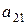 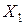 + + 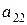 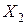 + … + + … + 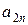 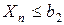 ,
……………………………………… ,
………………………………………
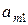 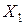 + + 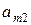 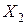 + … + + … + 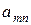 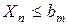 . .
|
и обращают функцию дохода 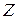 =
= 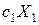 +
+ 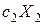 +…+
+…+ 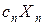 в максимум.
в максимум.
Транспортная задача.Пусть в пунктах 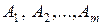 производится некоторый однородный продукт, причем объем производства (мощность) в каждом пункте известен. Этот продукт потребляется в пунктах
производится некоторый однородный продукт, причем объем производства (мощность) в каждом пункте известен. Этот продукт потребляется в пунктах 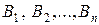 , при этом известен объем потребления (спрос) для каждого пункта. Предполагается, что суммарная мощность совпадает с суммарным спросом. Допустим, что транспортировка возможна из любого пункта производства в каждый пункт потребления, причем транспортные издержки, приходящиеся на единицу продукта, считаются заданными. (Под транспортными издержками понимают время перевоза, расстояние, стоимость).
, при этом известен объем потребления (спрос) для каждого пункта. Предполагается, что суммарная мощность совпадает с суммарным спросом. Допустим, что транспортировка возможна из любого пункта производства в каждый пункт потребления, причем транспортные издержки, приходящиеся на единицу продукта, считаются заданными. (Под транспортными издержками понимают время перевоза, расстояние, стоимость).
Транспортная задача заключается в распределении производимого продукта так, чтобы спрос был удовлетворен и суммарные транспортные издержки были минимальными.
Введем обозначения:
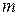 – –
| число поставщиков; |
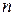 – –
| число потребителей; |
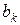 – –
| общее количество единиц продукта, необходимое 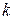 -му потребителю -му потребителю 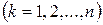 ; ;
|
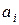 – –
| общее количество единиц продукта, выделяемое для перевозки 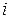 -м поставщиком -м поставщиком 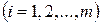 ; ;
|
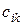 – –
| транспортные издержки, приходящиеся на единицу продукта, при перевозке из 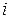 -го пункта в -го пункта в 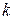 -ый пункт -ый пункт 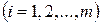 , , 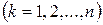 . .
|
Составим таблицу. Она даст нам более четкое представление о задаче.
Таблица 2
| Пункты производства | Объем производства | Транспортные издержки на одно изделие | |||
| Пункты потребления и спрос | |||||
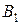
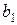
| 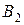
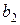
| …… | 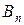
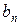
| ||
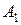
| 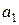
| 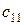
| 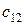
| … | 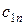
|
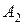
| 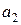
| 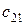
| 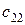
| … | 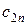
|
| … | … | … | … | … | … |
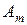
| 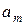
| 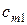
| 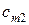
| … | 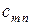
|
Особенностью транспортной задачи является наличие большого числа переменных, поэтому имеет смысл ввести двойные индексы. Обозначим через 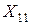 – количество продукта, перевозимого из первого пункта производства в первый пункт потребления, через
– количество продукта, перевозимого из первого пункта производства в первый пункт потребления, через 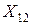 – количество продукта, перевозимого из первого пункта производства во второй пункт потребления, и т.д.,
– количество продукта, перевозимого из первого пункта производства во второй пункт потребления, и т.д., 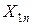 – количество продукта, перевозимого из
– количество продукта, перевозимого из 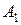 в
в 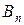 (первый индекс указывает номер пункта производства, второй – номер пункта потребления). Аналогично из второго пункта производства мы вывезем
(первый индекс указывает номер пункта производства, второй – номер пункта потребления). Аналогично из второго пункта производства мы вывезем
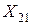 – –
| в первый пункт потребления; |
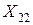 – –
| во второй пункт потребления; |
| ……………………………………….. | |
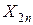 – –
| в 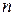 -ый пункт потребления. -ый пункт потребления.
|
Подобно предыдущему, для всех пунктов производства введем свои неизвестные. В частности, для последнего
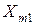 – из
– из 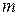 -го пункта в первый;
-го пункта в первый;
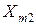 – из
– из 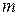 -го пункта во второй;
-го пункта во второй;
……………………………………
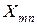 – из
– из 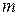 -го пункта в
-го пункта в 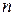 -ый.
-ый.
При этом по-прежнему первый индекс у неизвестного указывает номер пункта отправки, а второй – номер пункта потребления. То есть 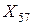 означает количество продукции, перевозимой из пятого пункта производства в седьмой пункт потребления.
означает количество продукции, перевозимой из пятого пункта производства в седьмой пункт потребления.
Составим ограничения. Прежде всего учтем, что общий спрос равен общему предложению, т.е.
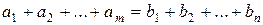 .
.
Исходя из введенных обозначений, получим, что величина 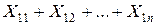 выражает собой не что иное, как количество единиц продукта, вывезенного из первого пункта производства во все пункты потребления. А так как продукт, имеющийся в этом пункте, должен быть распределен полностью без остатка, то, очевидно, эта сумма должна равняться имеющемуся запасу продукта, т.е.
выражает собой не что иное, как количество единиц продукта, вывезенного из первого пункта производства во все пункты потребления. А так как продукт, имеющийся в этом пункте, должен быть распределен полностью без остатка, то, очевидно, эта сумма должна равняться имеющемуся запасу продукта, т.е.
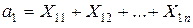 .
.
Рассуждая аналогично предыдущему, получим, что величина 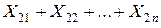 характеризует количество единиц продукта, перевозимого из второго пункта производства во все пункты потребления и т.д.; величина
характеризует количество единиц продукта, перевозимого из второго пункта производства во все пункты потребления и т.д.; величина 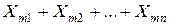 указывает, сколько единиц продукта вывезено из
указывает, сколько единиц продукта вывезено из 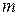 -го пункта производства во все пункты потребления. И эти величины также должны согласовываться с мощностью соответствующего поставщика.
-го пункта производства во все пункты потребления. И эти величины также должны согласовываться с мощностью соответствующего поставщика.
В итоге получим систему, отражающую интересы поставщиков
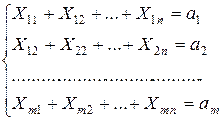 (1)
(1)
Однако эта система никак не учитывает интересы потребителей, ведь совсем не безразлично, сколько куда везти. Необходимо удовлетворить спрос потребителей. С этой целью будем подсчитывать, сколько в какой пункт мы везем от всех поставщиков. Так, в первый пункт мы везем от первого поставщика 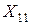 , от второго –
, от второго – 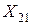 и т.д. от
и т.д. от 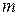 -го –
-го – 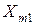 . Количество продукта, завезенного от всех поставщиков, должно совпадать с величиной спроса – объема потребления. Подобно этому, во второй пункт потребления мы перевозим
. Количество продукта, завезенного от всех поставщиков, должно совпадать с величиной спроса – объема потребления. Подобно этому, во второй пункт потребления мы перевозим 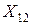 из первого пункта производства,
из первого пункта производства, 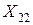 – из второго пункта производства и т.д.
– из второго пункта производства и т.д. 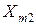 – из
– из 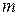 -го пункта производства. Сумма этих величин должна равняться объему потребления во втором пункте. Такого рода рассуждения приведут в тому, что в
-го пункта производства. Сумма этих величин должна равняться объему потребления во втором пункте. Такого рода рассуждения приведут в тому, что в 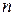 -ый пункт назначения мы перевозим величину
-ый пункт назначения мы перевозим величину 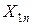 из первого пункта производства,
из первого пункта производства, 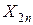 – из второго пункта и т.д.
– из второго пункта и т.д. 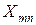 – из
– из 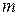 -го пункта.
-го пункта.
Таким образом, нами получена еще одна система, которая отражает интересы потребителей
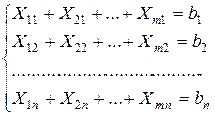 (2)
(2)
Естественно, что все введенные нами неизвестные не могут принимать отрицательных значений, т.е. 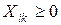
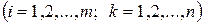 .
.
Общие транспортные издержки будут складываться из затрат, возникающих при перевозке из каждого пункта производства в каждый пункт потребления необходимого количества единиц продукта. Суммарные издержки могут быть выражены с помощью функции цели следующего вида:
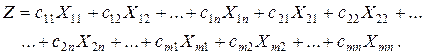
Итак, наша задача заключается в нахождении таких неотрицательных величин 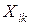 , которые удовлетворяли бы системам (1) и (2), а целевая функция
, которые удовлетворяли бы системам (1) и (2), а целевая функция 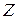 была бы минимальной.
была бы минимальной.
Задача о смесях.К этим задачам относятся задачи оптимального состава шихты для получения стали, задачи о смесях продукции, задачи диеты и др.
Рассмотрим задачу диеты. Предположим, что имеются различные пищевые продукты. Известна цена единицы каждого продукта и количество жизненно необходимых питательных веществ в единице каждого продукта. Кроме того, считается заданной величина, выражающая ежесуточную потребность в каждом питательном веществе.
Нужно составить диету, которая обеспечивала бы ежесуточную потребность организма в каждом питательном веществе при наименьшей стоимости используемых продуктов.
Примем следующие обозначения:
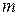 – –
| число питательных веществ, необходимых организму; |
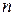 – –
| число имеющихся пищевых продуктов; |
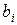 – –
| минимальная ежесуточная потребность в 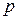 -м веществе -м веществе 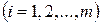 ; ;
|
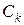 – –
| цена единицы продукта 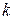 -ого вида -ого вида 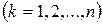 ; ;
|
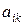 – –
| количество 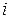 -ых питательных веществ в единице -ых питательных веществ в единице 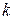 -го продукта. -го продукта.
|
Данные задачи запишем в таблицу. Она будет иметь следующий вид.
Таблица 3
| Виды питательных веществ | Содержание питательных веществ
в единице 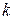 -го продукта -го продукта
| Потребность в питательных веществах | |||
| В и д ы п р о д у к т о в | |||||
| 1 | 2 | … | 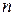
| ||
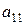
| 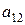
| … | 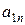
| 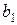
| |
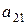
| 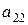
| … | 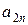
| 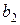
| |
| … | … | … | … | … | … |
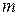
| 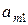
| 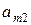
| … | 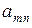
| 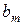
|
Стоимость
единицы продукта
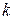 -го вида -го вида
| 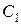
| 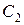
| … | 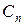
| 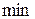
|
Таблица в этой задаче по внешнему виду полностью совпадает с таблицей задачи производственного планирования, однако по смыслу задачи не идентичны. Обозначим через:
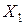 – –
| количество единиц первого продукта, входящее в диету; |
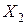 – –
| количество единиц второго продукта; |
| и т.д. | |
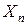 – –
| количество единиц 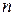 -го продукта. -го продукта.
|
В единице продукта первого вида содержится 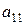 единиц первого питательного вещества, а во всем первом продукте этого вещества будет
единиц первого питательного вещества, а во всем первом продукте этого вещества будет 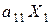 . Этого же питательного вещества в единице продукта второго вида содержится
. Этого же питательного вещества в единице продукта второго вида содержится 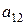 единиц, тогда содержание первого питательного вещества во всем количестве 2-го продукта выразится величиной
единиц, тогда содержание первого питательного вещества во всем количестве 2-го продукта выразится величиной 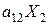 . Вычисляя величины
. Вычисляя величины 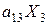 – количество первого вещества во всем продукте третьего вида – и т.д., и, наконец,
– количество первого вещества во всем продукте третьего вида – и т.д., и, наконец, 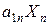 – количество вещества первого вида во всем
– количество вещества первого вида во всем 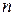 -ом продукте, мы можем найти общее количество первого питательного вещества, содержащегося во всех продуктах. Оно будет равно:
-ом продукте, мы можем найти общее количество первого питательного вещества, содержащегося во всех продуктах. Оно будет равно:
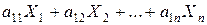 .
.
Нам не безразлично, какой будет эта величина, она должна удовлетворять ежесуточную потребность в рассматриваемом веществе, т.е. она должна быть не менее ежесуточной нормы. Получаем ограничение
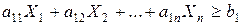 .
.
Рассмотрим второе питательное вещество. Следует учесть содержание этого вещества во всем количестве первого продукта, второго и т.д., 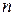 -го продукта. Суммируя отдельные значения количества единиц второго питательного вещества во всех продуктах каждого вида, получим общее количество второго питательного вещества. Оно, естественно, должно быть не менее ежесуточной потребности в этом веществе. Получим еще одно ограничение. Аналогично предыдущему, можно установить соотношения между содержанием питательного вещества любого вида во всех продуктах и потребностью в этом веществе. В результате придем к системе ограничений
-го продукта. Суммируя отдельные значения количества единиц второго питательного вещества во всех продуктах каждого вида, получим общее количество второго питательного вещества. Оно, естественно, должно быть не менее ежесуточной потребности в этом веществе. Получим еще одно ограничение. Аналогично предыдущему, можно установить соотношения между содержанием питательного вещества любого вида во всех продуктах и потребностью в этом веществе. В результате придем к системе ограничений
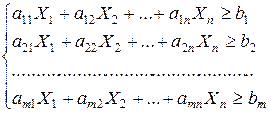
Величины 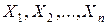 , выражающие собой количество продукта соответственно первого, второго и т.д.,
, выражающие собой количество продукта соответственно первого, второго и т.д., 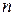 -го вида, не могут быть отрицательными. В крайнем случае какие-то из них могут равняться нулю (это будет означать, что данный продукт не входит в рацион питания).
-го вида, не могут быть отрицательными. В крайнем случае какие-то из них могут равняться нулю (это будет означать, что данный продукт не входит в рацион питания).
Зная, что цена единиц продукта первого вида равна 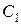 , можем вычислить стоимость всего первого продукта – она равна
, можем вычислить стоимость всего первого продукта – она равна 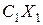 . По тем же соображениям стоимость всего второго продукта равна
. По тем же соображениям стоимость всего второго продукта равна 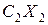 и т.д., стоимость
и т.д., стоимость 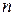 -го продукта равна
-го продукта равна 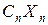 . Суммарная стоимость всех продуктов, используемых в диете, равна сумме этих всех стоимостей. И задача диеты заключается в нахождении величин
. Суммарная стоимость всех продуктов, используемых в диете, равна сумме этих всех стоимостей. И задача диеты заключается в нахождении величин 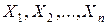 , которые удовлетворяют ограничениям
, которые удовлетворяют ограничениям
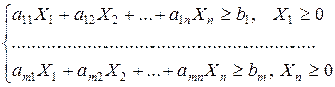
и дают минимум целевой функции
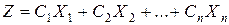 .
.
Основная задача линейного программирования.Мы рассмотрели несколько примеров построения моделей линейного программирования. В каждой из этих моделей задача состояла в нахождении решения системы линейных уравнений или неравенств, минимизирующего или максимизирующего линейную целевую функцию.
Основной математической задачей линейного программирования называется оптимизация линейной формы при линейных ограничениях. Все задачи линейного программирования можно сформулировать одним и тем же способом, а именно: найти в неотрицательных числах решение системы линейных уравнений, которое минимизирует функцию цели. Такая форма задачи называется канонической. Другими словами, найти 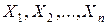 , чтобы выполнялись ограничения
, чтобы выполнялись ограничения
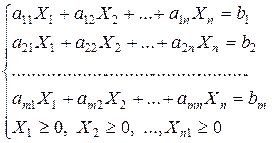
и минимизировалась величина
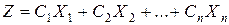 .
.
При использовании задач линейного программирования могут встретиться случаи:
1. Система ограничений противоречива, задача не имеет неотрицательных решений.
2. Система ограничений имеет неотрицательные решения, но максимум (минимум) функции цели равен 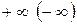 .
.
3. Значение максимума (минимума) целевой функции конечно, система ограничений имеет неотрицательные решения.
Для задач линейного программирования, связанных с реальными практическими проблемами, обычно имеет место третий случай.
Значение 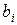
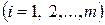 считают неотрицательным, в противном случае соответствующее уравнение можно умножить на (–1). Кроме того, ограничения – неравенства можно представить в форме уравнений путем введения дополнительных переменных; чтобы не нарушалось условие неотрицательности, дополнительные неизвестные берут со знаком плюс или минус в зависимости от того, левая часть неравенства меньше правой или больше ее. Так, например, в задаче производственного планирования в каждое ограничение следует прибавить дополнительную переменную, и задача примет вид:
считают неотрицательным, в противном случае соответствующее уравнение можно умножить на (–1). Кроме того, ограничения – неравенства можно представить в форме уравнений путем введения дополнительных переменных; чтобы не нарушалось условие неотрицательности, дополнительные неизвестные берут со знаком плюс или минус в зависимости от того, левая часть неравенства меньше правой или больше ее. Так, например, в задаче производственного планирования в каждое ограничение следует прибавить дополнительную переменную, и задача примет вид:
Найти неотрицательные 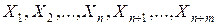 , которые удовлетворяют условиям , которые удовлетворяют условиям
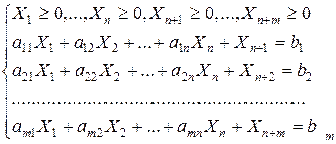 и обращают в максимум линейную форму
и обращают в максимум линейную форму
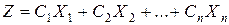 .
Здесь .
Здесь 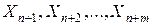 – дополнительные переменные. – дополнительные переменные.
|
А в задаче о смесях в каждом ограничении нужно вычесть дополнительную переменную.
Задача производственного планирования отличается от транспортной и задачи о диете тем, что в ней необходимо найти максимум линейной формы. Это отличие можно считать несущественным, учитывая, что от максимума целевой функции 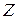 при некоторых ограничениях легко перейти к нахождению минимума функции
при некоторых ограничениях легко перейти к нахождению минимума функции 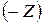 , а после полного решения произвести обратный переход. И действительно, если величина
, а после полного решения произвести обратный переход. И действительно, если величина 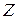 приняла максимальное значение, то величина, ей противоположная, т.е.
приняла максимальное значение, то величина, ей противоположная, т.е. 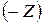 , примет наименьшее значение (самое большое по абсолютной величине, но со знаком минус).
, примет наименьшее значение (самое большое по абсолютной величине, но со знаком минус).
Если условие неотрицательности не вытекает из физического смысла переменных, то каждую из переменных представляют в виде разности двух неотрицательных величин: 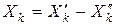 . В этом равенстве
. В этом равенстве 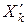 и
и 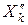 могут принимать только неотрицательные значения, а их разность, т.е.
могут принимать только неотрицательные значения, а их разность, т.е. 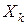 может принимать любые значения. Введя неотрицательные переменные
может принимать любые значения. Введя неотрицательные переменные 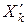 и
и 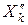 , мы выполнили важнейшее требование задач линейного программирования.
, мы выполнили важнейшее требование задач линейного программирования.
Сделаем несколько замечаний относительно математического моделирования экономических задач линейного программирования. Цель исследования должна быть четко определена и точно отражена в построении целевой функции. При этом следует учесть, что математическая модель конкретной экономической задачи может содержать только одну целевую функцию: в математической модели несовместимо наличие двух или нескольких целевых функций. Поэтому при качественном анализе задачи необходимо выделить для оптимизации один наиболее важный экономический показатель, а остальные показатели ограничить пределами допустимого уровня и ввести их в модель в качестве линейных ограничений. Кроме того, ограничения задачи должны быть полными и точно отражать все данные об экономических факторах, содержащихся в условии задачи. Построение математической модели экономической задачи – это процесс творческий. Чтобы уметь в каждом конкретном случае составить правильную, математически строгую формулировку задачи, нужны определенные навыки. И если математическая модель экономической задачи линейного программирования составлена, то она может быть решена одним из методов, рассматриваемых позднее. Рассмотрим несколько примеров построения математической модели.
Задача 1.В состав рациона кормления ребенка входят три продукта – смеси “Малыш”, “Крепыш”, “Силач”, содержащие витамины А, В, С. Содержание витаминов (в условных единицах на 100 г) соответствующего продукта, минимальные нормы их потребления, а также предельно допустимые количества смесей для ребенка в сутки заданы в таблице. Определить оптимальный рацион кормления ребенка из условия минимальной стоимости питания.
| Витамины Смеси | А | В | С | Нормы потребления смесей, г в сутки | Стоимость 100 г смесей, грн. |
| “Малыш” | 3,6 | 1,2 | |||
| “Крепыш” | 2,5 | 0,8 | |||
| “Силач” | 2,0 | 0,6 | |||
| Нормы потребления витаминов, усл.ед. | 24,0 | 8,0 |
Пусть 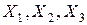 – количества смесей “Малыш”, “Крепыш”, “Силач” соответственно, приобретаемые для кормления ребенка в течение дня. В данном случае удобно выбрать в качестве единицы измерения пачку, содержащую 100 г смеси, так как смеси продаются в пачках и из условий задачи известна стоимость пачки каждого вида. К тому же содержание питательных веществ дается в граммах на 100 г смеси. Мы должны определить, сколько пачек детских смесей и в какой пропорции нужно приобрести ребенку на одни сутки.
– количества смесей “Малыш”, “Крепыш”, “Силач” соответственно, приобретаемые для кормления ребенка в течение дня. В данном случае удобно выбрать в качестве единицы измерения пачку, содержащую 100 г смеси, так как смеси продаются в пачках и из условий задачи известна стоимость пачки каждого вида. К тому же содержание питательных веществ дается в граммах на 100 г смеси. Мы должны определить, сколько пачек детских смесей и в какой пропорции нужно приобрести ребенку на одни сутки.
Общие запасы витамина А во всех трех видах смесей составляют 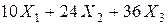 граммов и не должна быть меньше 200 ед., то есть минимально необходимой нормы его потребления в сутки. Это требование приводит к неравенству
граммов и не должна быть меньше 200 ед., то есть минимально необходимой нормы его потребления в сутки. Это требование приводит к неравенству
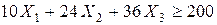 .
.
Знак неравенства (а не точного равенства) возникает потому, что ребенок может получить и большее количество витамина А, чем предписано минимальной нормой его потребления. Аналогичные рассуждения относительно потребления витаминов В и С приводят к следующим двум неравенствам:
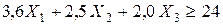 ,
,
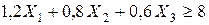 .
.
Далее для ребенка существуют предельные нормы потребления в сутки; они заданы по каждой из смесей и порождают неравенства:
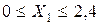 ;
; 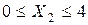 ;
; 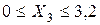 .
.
(Левые стороны неравенств получены из условий неотрицательности выбранных нами переменных; при написании неравенств учтена также размерность переменных).
Стоимость питания ребенка будет составлять 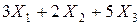 грн. в сутки и должна быть минимальной. Из этого условия определяется целевая функция задачи.
грн. в сутки и должна быть минимальной. Из этого условия определяется целевая функция задачи.
Итак, мы пришли к математической модели, включающей систему из шести линейных неравенств и линейную функцию относительно трех неизвестных:
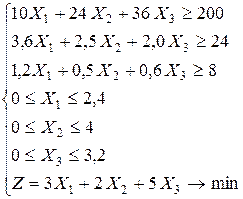
Требуется среди всех неотрицательных решений системы линейных неравенств найти такое, которое минимизирует функцию 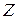 .
.
Задача 2.Предприятие может работать по пяти технологическим процессам, причем количество единиц выпускаемой продукции по разным технологическим процессам за 1 ед. времени соответственно равно 300, 260, 320 и 450 шт. В процессе производства учитываются следующие производственные факторы: сырье, электроэнергия, зарплата и накладные расходы. Затраты соответствующих факторов (в тыс. грн.) при работе по указанным технологическим процессам в течение 1 ед. времени указаны в следующей таблице. Найти программу максимального выпуска продукции.
| Технологические процессы Производственный факторы | Ресурсы, тыс.грн. | |||||
| Сырье | 12,0 | 15,0 | 10,0 | 12,0 | 11,0 | |
| Электроэнергия | 0,2 | 0,1 | 0,2 | 0,25 | 0,5 | |
| Зарплата | 3,0 | 4,0 | 5,0 | 5,0 | 2,0 | |
| Накладные расходы | 6,0 | 5,0 | 4,0 | 6,0 | 4,0 |
В последней графе таблицы указаны ресурсы в тыс. грн., которыми располагает предприятие по каждому из производственных факторов. Составим математическую модель задачи. Прежде всего определим, что подразумевается под программой максимального выпуска продукции. На предприятии выпускается один вид продукции, для производства которой могут применяться пять различных технологических процессов. Можно планировать либо выпуск продукции (в шт.) по каждому технологическому процессу в отдельности, либо время работы предприятия по каждому технологическому процессу. В данной задаче для написания математической модели удобнее выбрать второй путь – все условия задачи сформулированы в пересчете на единицу времени работы предприятия. Зная из условий задачи количество единиц продукции, выпускаемой по разным технологическим способам в единицу времени, и определив в результате ее решения время работы предприятия по тому или иному технологическому процессу, мы найдем “технологическую” структуру выпуска продукции на предприятии. Таким образом, переменные математической модели будут такими: 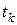 – это количество времени, в течение которого предприятие будет выпускать продукцию по
– это количество времени, в течение которого предприятие будет выпускать продукцию по 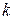 -му технологическому процессу.
-му технологическому процессу.
Заметим, что общее время работы предприятия, как и время работы по любому из технологических процессов, в условиях задачи не ограничено. Выпуск продукции лимитируют лишь производственные факторы. Предположим, что каждый из технологических процессов будет использован при производстве продукции. Тогда общие затраты, например, электроэнергии для осуществления производственной программы составят 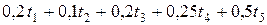 грн. и по условию не должны превышать 30000 грн. Так пр
грн. и по условию не должны превышать 30000 грн. Так пр
Дата добавления: 2022-07-20; просмотров: 186;











