Определение спецификации корреляционной зависимости

В ходе статистического анализа социально-экономических явлений часто возникает необходимость выявления и оценки взаимосвязей между статистическими признаками. При этом один из признаков полагают зависимым от других и называют результативным, а остальные – факторными.

Различают два вида зависимости – функциональную и корреляционную. При строгой функциональной зависимости каждому сочетанию значений факторных признаков соответствует только одно значение результативного признака. Например, товарооборот торгового предприятия в рамках отдельного товара всегда равен произведению его цены на физический объём продаж.

При корреляционной зависимости изменение значений факторных признаков влечет изменение распределения значений результативного признака с изменением его среднего значения. В отличие от функциональной зависимости, корреляционная связь проявляется не в каждом случае, а в среднем при большом числе единиц наблюдения. Например, урожай зерна находится в корреляционной зависимости от площади участка земли и количества удобрений, внесенных на единицу этой площади. При одном и том же количестве удобрений, внесенных на единицу площади одинаковых по размеру участков земли, будет наблюдаться разный урожай. Это объясняется влиянием случайных факторов, таких как количество осадков, средняя температура воздуха и др. Вместе с тем, как показывает опыт, средняя величина урожая в основном определяется именно площадью земельного участка и количеством внесенных удобрений.

По числу факторных признаков выделяют парную и множественную корреляционную зависимости. Парная корреляция рассматривается в случае, когда доминирующее влияние на результат оказывает только один фактор. Например, величина расходов домашних хозяйств корреляционно зависит в основном только от их доходов. При множественной корреляции имеется два или более фактора, совместно существенно влияющих на результат. При этом в отношении каждого из факторов оценивают частную корреляцию – зависимость результата от этого фактора при фиксированных значения других факторов.

Парная (частная) корреляция может быть прямой и обратной. При прямой корреляции рост значения факторного признака приводит к увеличению значения результата. При обратной корреляции – наоборот.

В зависимости от формы влияния факторов на результат различают прямолинейную (линейную) и криволинейную (нелинейную) корреляции.

Исследование корреляционных связей проводят на основе методов корреляционно-регрессионного анализа. Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты корреляции, определение ее направления и формы (вначале примерной – линейной или нелинейной, а затем точной – аналитически выраженной).

В рамках корреляционного анализа решают задачу количественной оценки тесноты связи между двумя признаками (при парной корреляции) или между результативными и факторными признаками (при множественной корреляции). Теснота связи выражается показателем корреляции, расчетная формула которого зависит от формы корреляции (линейная или нелинейная) и числа факторов (парная корреляция или множественная).

Одновременно с корреляционным анализом проводят регрессионный анализ, который заключается в определении аналитического выражения корреляционной связи. Для аналитического выражения корреляции используют уравнения регрессии, которые в соответствии со спецификацией исследуемой корреляции делятся на:

· линейные и нелинейные уравнения регрессии;

· уравнения парной и множественной регрессии.

При определении параметров уравнения регрессии используют метод наименьших квадратов, ориентируются на минимум суммы квадратов отклонений теоретических значений результативного признака (значений, рассчитываемых по уравнению регрессии) от его фактических значений.

Как уже отмечалось, деление корреляционно-регрессионного анализа на корреляционный и регрессионный является условным. В общем случае, в процессе изучения корреляционной зависимости попеременно используют и тот, и другой виды анализа. При этом соблюдается следующая последовательность действий:

1) определяют для рассматриваемого результативного признака полный перечень факторных признаков на основе теоретических знаний об исследуемом явлении;

2) выбирают спецификацию корреляционной зависимости результата от факторов (вид уравнения регрессии) – эмпирически (путем подбора уравнения регрессии, адекватного фактическим данным) или теоретически (на основе теоретических знаний об исследуемом явлении);

3) исключают из рассмотрения факторы, влияние которых на результат является несущественным. При этом ориентируются на изменение адекватности уравнения при исключении отдельного фактора;

4) оценивают тесноту корреляционной зависимости результата от отобранных факторов в целом (оценка тесноты множественной корреляции) и по каждому фактору отдельно (оценка тесноты частной корреляции). При наличии только одного отобранного фактора (случай парной корреляции) эта процедура значительно упрощается;

5) определяют окончательные значения уравнения регрессии и оценивают его адекватность фактическим данным. В случае адекватности делают вывод о возможности применения уравнения на практике и экономически интерпретируют его параметры.

Выбор спецификации корреляционной зависимости фактически означает определение уравнения регрессии, описывающего зависимость результативного признака от факторных признаков с наименьшей погрешностью. Поскольку зависимость является не функциональной, а корреляционной, то при любом уравнении фактические значения результативного признака будут отличаться от теоретических значений из-за влияния неучтенных факторов:

,

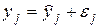где:

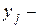фактическое значение результативного признака;

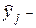его теоретическое значение, определяемое по уравнению регрессии;

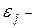случайная величина, характеризующая расхождение между фактическим и теоретическим значениями результативного признака.

В статистической практике для описания используют следующие спецификации корреляционных моделей:

· линейные уравнения

;

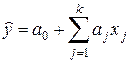· полиномы разных степеней (парабола, кубическая парабола и т. д.)

;

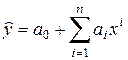· гиперболы

;

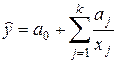· степенные уравнения

;

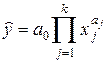· показательные уравнения

;

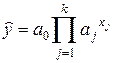· экспоненциальные уравнения

.

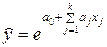Часть нелинейных уравнений являются внутренне линейными. Это означает, что то они могут быть математически преобразованы в линейные. Линеаризацию таких уравнений осуществляют путем замены результативного или факторных признаков на другие величины, связанные с ними функционально.

Например, экспоненциальное уравнение можно привести к линейному уравнению путем замены результативного признака на его натуральный логарифм:

.

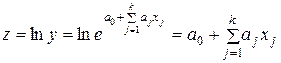При линеаризации уравнения гиперболы исходные факторные признаки заменяют на обратные величины:

.

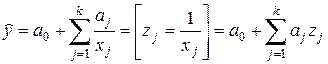Линеаризация парной регрессии, представленной в виде полинома произвольной степени, осуществляется путем перехода к множественной регрессии:

.

Для выбора конкретной спецификации корреляции используют различные методы. Если перечень факторов ограничивается только одним признаком (случай парной корреляции), то вид спецификации можно определить графически путем построения корреляционного поля или эмпирической кривой. В первом случае в прямоугольной системе координат (х, у) отображают точками все пары фактических значений результирующего и факторного признаков. Во втором случае значения фактора распределяют по вариантам и для каждого варианта рассчитывают среднее значение результата. Полученные пары значений изображают в виде точек, которые соединяют отрезками (при распределении значений фактора по интервалам используют середины этих интервалов).

Если при построении корреляционного поля или эмпирической кривой выясняется, что корреляция имеет однозначное направление (прямое или обратное) и близка к прямой линии, то следует использовать линейную спецификацию. В противном случае корреляционную зависимость следует считать нелинейной.

Парабола второй степени целесообразна к применению, когда нелинейная корреляция однократно меняет свое направление (прямое на обратное или обратное на прямое). Не рекомендуется использовать параболу только на одном из ее участков, поскольку это может осложнить экономическую интерпретацию ее параметров. В этом случае следует применить другую форму нелинейной корреляции и выбрать в качестве спецификации гиперболическое, степенное, показательное или экспоненциальное уравнение.

При исследовании множественной корреляции использование графического метода не приемлемо, поскольку форма корреляции результата и фактора искажается одновременным изменением значений других факторов. В этом случае для определения спецификации может быть использован теоретический метод, основанный на знании экономического содержание анализируемых связей. Например, зная суть хозяйственной деятельности предприятий, производящих качественно однородные товары, и исследуя корреляционную зависимость объема производимой предприятием продукции от стоимости его основных производственных фондов и расхода оборотных средств, следует выбрать линейную спецификацию.

Независимо от количества факторов спецификацию корреляционной зависимости можно определить эмпирически, перебирая по специально разработанному алгоритму различные уравнения и выбирая одно из них, наиболее адекватно описывающее фактические значения результирующего признака. При небольшом числе факторов этот метод можно реализовать вручную, но в общем случае для этого необходимо использование ЭВМ.