Имитационное моделирование. Цели

Имитация — это попытка дублировать особенности, внешний вид и характеристики реальной системы. Идея имитации реали­зуется следующим образом:

1) математическое описание реальной ситуации;

2) изучение ее свойств и особенностей;

3) формирование выводов и принятие решений, связанных с воздействием на эту ситуацию и основанных на результатах имитации.

Важно, что реальная система не подвергается воздействию до тех пор, пока преимущества или недостатки тех или иных управ­ленческих решений не будут оценены с помощью модели этой системы.

После того как вы выполните задания, предлагаемые в этой главе, вы. будете уметь использовать для экономического ана­лиза:

• имитацию;

• интервал случайных чисел;

• метод Монте-Карло;

• таблицу случайных чисел.

Модели. Метод Монте-Карло (метод статистических испытаний) состо­ит из четырех этапов:

1. Построение математической модели системы, описывающей зависимость моделируемых характеристик от значений стохасти­ческих переменных.

2. Установление распределения вероятностей для стохастичес­ких переменных.

3. Установление интервала случайных чисел для каждой сто­хастической переменной и генерация случайных чисел.

4. Имитация поведения системы путем проведения многих ис­пытаний и получение оценки моделируемой характеристики си­стемы при фиксированных значениях параметров управления. Оценка точности результата.

Описание этапов:

Первый этап. Стохастическая имитационная модель (ИМ) не­которой реальной системы может быть представлена как динами­ческая система, которая под воздействием внешних случайных входных сигналов (входных переменных) изменяет свое состояние (случайные переменные состояния), что в свою очередь приводит к изменению выходных сигналов (выходных переменных):

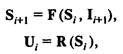
гдеF, R — вектор-функции;

I_i, U_i, S_i — векторы соответственно входных, выходных пере­менных и переменных состояния системы в так­товый момент моделирования i.

Имитационная модель — это экспериментальная модель систе­мы, в которой искусственно воспроизводятся случайности, име­ющие место в реальной системе. Она представляет собой совокуп­ность математических соотношений между входными, выходными переменными и переменными состояния в сочетании с алгорит­мической реализацией некоторых зависимостей.

Существует два подхода в имитационном моделировании ди­намических процессов.

Первый заключается в том, что весь период моделирования разбивается на равные промежутки времени (такты моделирова­ния) и анализ состояния системы, а также значений выходных переменных производится через одинаковые промежутки време­ни. При таком подходе возникает проблема выбора «правильной» продолжительности такта. Кроме того, не исключается появление тактов, в которых состояние системы по сравнению с предыдущим не изменилось.

При втором подходе величина такта моделирования не фик­сируется, моделирование в этом случае происходит в момент на­ступления одного из «существенных» событий. Например, при моделировании производственного процесса на предприятии та­кими событиями могут быть освобождение или начало загрузки станка, поступление на обработку детали, невыход на работу ста­ночника, исчерпание запаса необходимых комплектующих дета­лей на складе и др. Именно второй подход чаще всего использу­ется на практике и поддерживается современными языками мо­делирования.

Второй этап. Случайные величины, используемые в ИМ, мо­гут быть дискретными или непрерывными. В первом случае не­обходимо знать их распределения, во втором — плотности распре­делений. Эти зависимости могут быть известны из теории, опре­делены в результате специальных исследований либо заданы в качестве гипотезы. Точность модели (при прочих равных услови­ях) зависит от того, насколько точно заданы указанные распреде­ления (плотности распределений).

Третий этап. Моделирование случайных величин при компью­терных имитационных экспериментах производится с помощью датчика псевдослучайных чисел, предусмотренного в любом со­временном языке программирования. Обычно это датчик случай­ных чисел с равномерным распределением на интервале [0, 1]. Если известны вероятности наступления событий, то, используя такой датчик, можно отвечать на вопросы: «Какое из N возмож­ных событий произошло?» или «Какое значение приняла случай­ная величина?»

Предположим, что в ИМ используется случайная величина X, принимающая дискретные значения х₁, х₂,..., х_N с вероятностями соответственно p₁, p₂,..., p_N ( 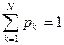). Получение некоторой реализации этой переменной в модели производится следующим образом.

Строится функция распределения случайной величины X. Ука­занная функция определяется посредством равенства F(X) = åp_k, в котором суммирование распространяется на все индексы, для которых х_k < X. С помощью датчика случайных чисел получают случайное число и из отрезка [0, 1].

Из равномерности распределения получаемых случайных чи­сел следует, что вероятность получения случайного числа из про­извольного интервала, включенного в [0, 1], равна длине этого интервала. Поэтому вероятность реализации Х = х_k равна веро­ятности попадания полученного от датчика случайного числа и в произвольный интервал длиной p_k на отрезке [0, 1]. Можно, та­ким образом, утверждать, что если очередное число и датчика удовлетворяет неравенствам 0 < и £ р₁, то имеет место реализа­ция Х = х₁, в случае p₁ < и £ p₁ + р₂ — реализация Х = х₂ и т.д. 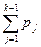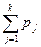В общем случае для k = 2, ..., N: если < и £ , то Х = х_k.

Заметим, что границы указанных неравенств совпадают со зна­чениями построенной выше функции распределения F(X).

Удобнее, однако, иметь дело не с дробными значениями гра­ниц интервалов, в которые попадает случайное число и, а с их целочисленными значениями, тем более, что с помощью датчи­ков случайных чисел можно генерировать числа из любого диа­пазона. Чтобы получить целые значения границ интервалов, до­статочно умножить все p_k на 10^d, где d — целое, минимальное зна­чение которого равно максимальной точности (максимальному числу знаков после десятичной точки) чисел p_k, k = 1,..., N. На­пример, если {р_k} = {0,3; 0,153; 0,5; 0,047}, то минимальное зна­чение d равно 3 (все р_k нужно умножить на 1000). Таким образом, 10^d определяет длину интервала значений рассматриваемой слу­чайной величины в ИМ.

Четвертый этап. Точность статистических оценок параметров реальной системы зависит от числа наблюдений (объема выбор­ки). Погрешности в оценках обусловлены как статистическим характером самой модели, так и влиянием начальных данных (на­чального состояния имитационной системы), а также возможной автокорреляцией последовательных значений некоторого парамет­ра в процессе моделирования. Очевидно, что с увеличением чис­ла испытаний точность моделирования должна возрастать. Ввиду того что увеличение объема выборки связано с ростом затрат на моделирование, важно уметь определять минимальное число ис­пытаний, необходимое для достижения заданной точности оцен­ки с заданной вероятностью.

Широкое распространение получили два метода статистичес­ких испытаний. Один из них предполагает проведение достаточ­но большого числа Т последовательных наблюдений в течение одного прогона модели (одного сеанса имитирования).

Другой метод заключается в реализации т независимых про­гонов модели, т.е. в m-кратном повторении одного и того же цикла имитирования. При этом, если мы хотим получить в сумме Т наблюдений, в течение каждого прогона можно делать по Т/т (допустим, что это число целое) наблюдений. Оба метода дают примерно одинаковый результат.

Пусть значения у_t (t = 1,..., Т) представляют собой результа­ты Т последовательных измерений значений случайной величи­ны y во время одного и того же сеанса имитации. Среднее по вре­мени значение у определяется выражением

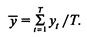
Обозначим через m математическое ожидание случайной вели­чины у. Тогда для достаточно большого T получаем

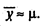
Оценка дисперсии 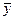(если временной ряд не является авто­коррелированным) имеет вид

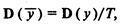
где D(у) — дисперсия случайной величины у.

Для оценки качества результатов, полученных методом Мон­те-Карло при неизвестной дисперсии наблюдаемой случайной величины, предположим, что Z — характеристика, которая долж­на быть определена (вероятность события, математическое ожи­дание, дисперсия и т.п.), a x — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограни­ченности числа T проведенных наблюдений. В этих условиях мож­но говорить о вероятности p(|Z – x| < e) по отношению к инте­ресующей нас характеристике. Величина |Z – e| представляет со­бой погрешность в оценке Z, a e — некоторый допустимый ее предел.

Из неравенства Чебышёва следует

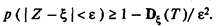
Из этого неравенства следует

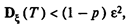
откуда при заданных р и e и при известной зависимости D_e (Т)можно найти предельно необходимое Т.

Известно, что истинная дисперсия выборочного распределения для расчетного среднего обратно пропорциональна суммарному числу наблюдений Т, т.е.

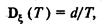
где d не зависит от Т.

В начале имитационного процесса требуемое число наблюде­ний определить обычно не удается, поскольку d неизвестно. По­этому, как правило, эксперимент проводят в два этапа.

На первом этапе число испытаний выбирается относительно небольшим, в результате определяется величина d. После этого можно уже определить, сколько дополнительных наблюдений необходимо, чтобы была достигнута требуемая точность.

Предельное число наблюдений Т₀ определяется формулой T₀ = d/[(1 – p)e²].

При любом числе наблюдений больше Т₀ обеспечивается тре­буемая точность.

Примеры. Пример 1. Моделирование объема спроса на автомашины.

Наблюдения за объемом продаж автомобилей в салоне «ЛОГОВАЗ» в течение 200 дней показали, что величина спроса изменяется от 0 до 5 автомобилей в день. Частота реализации значений стохас­тической переменной приведена во втором столбце таблицы:

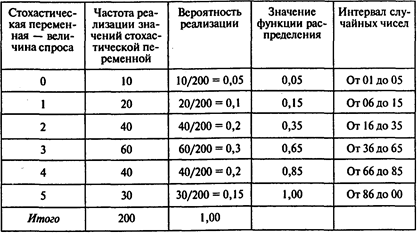
Постройте модель, позволяющую имитировать значение вели­чины спроса.

Решение. Построим функцию распределения величины спроса и интервалы случайных чисел для значений стохастической пере­менной. Соответствующие значения указаны в четвертом и пятом столбцах вышеприведенной таблицы.

Сымитируем спрос на автомашины в салоне «ЛОГОВАЗ» в те­чение 10 последующих дней (случайные числа из таблицы случай­ных чисел (Приложение 2) выбираем, начиная из верхнего лево­го угла и двигаясь вниз в первом столбце):

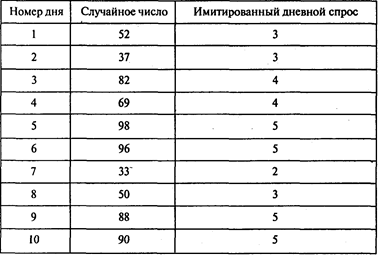
В результате получаем: 39 — спрос за 10 дней; 39/10 = 3,9 — средний ежедневный спрос.

Оценка 3,9 средней величины спроса, полученная в результате имитационного эксперимента, существенно отличается от значе­ния 2,95 — математического ожидания этой случайной величины. Однако эта разница уменьшается с ростом числа испытаний.

Пример 2. Моделирование очереди на разгрузку.

Груженые баржи, отправляемые вниз по Волге из индустри­альных центров, достигают Астрахани. Число барж, ежедневно входящих в док, колеблется от 0 до 5. Вероятность прихода 0, 1,..., 5 барж показана в таблице:

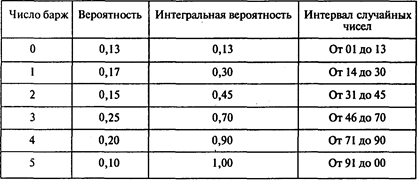
В этой же таблице указаны интегральные вероятности и соот­ветствующие интервалы случайных чисел для каждого возможного значения.

Аналогичная информация дана о числе разгружаемых барж:

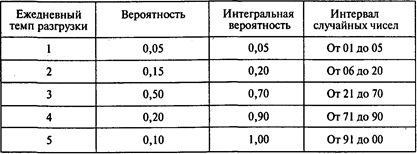
Постройте модель, позволяющую имитировать очередь на раз­грузку.

Решение. Проведем эксперимент, имитирующий очередь на разгрузку барж в порту Астрахани:

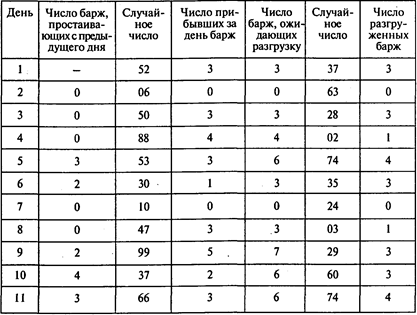
Окончание таблицы

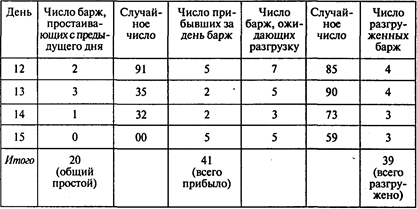
В результате эксперимента получены:

оценка среднего числа барж, простаивающих в течение суток, равная ²⁰/₁₅;

оценка среднего числа барж, прибывающих в течение суток, равная ⁴¹/₁₅;

оценка среднего числа барж, разгруженных в течение суток, равная ³⁹/₁₅.

Пример 3. Имитация стратегии резервирования.

Магазин электрооборудования продает электрические дрели. В течение 300 дней директор магазина Проводков регистрировал дневной спрос на дрели. Распределение вероятностей величины спроса показано в таблице:

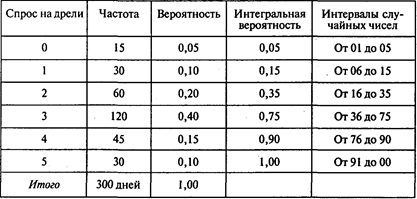
Когда Проводков делает заказ, чтобы возобновить свои запа­сы электрических дрелей, его выполнение происходит с лагом в 1, 2 или 3 дня. Это означает, что время восстановления запаса подчиняется вероятностному распределению. В следующей табли­це указаны сроки, вероятности сроков выполнения заказов и ин­тервалы случайных чисел, которые удалось определить на основе информации о 50 заказах:

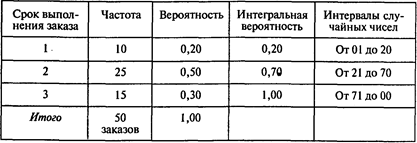
Стратегия резервирования, которую хочет имитировать Про­водков, — делать заказ в объеме 10 дрелей при запасе на складе 5 шт. Проводков оценил, что каждый заказ на дрели обходится ему в 10 руб., хранение каждой дрели — в 5 руб. в день, одна упущен­ная продажа — в 80 руб. Цель эксперимента — оценить величину средних ежедневных затрат для этой стратегии управления запа­сами.

Решение. Реализуется четырехшаговый процесс имитации:

1. Каждый имитируемый день начинается с проверки, посту­пил ли сделанный заказ. Если заказ выполнен, то текущий запас увеличивается на величину заказа (в данном случае — на 10 еди­ниц).

2. Путем выбора случайного числа генерируется дневной спрос для соответствующего распределения вероятностей.

3. Рассчитывается итоговый запас, равный исходному запасу за вычетом величины спроса. Если запас недостаточен для удовлет­ворения дневного спроса, спрос удовлетворяется, насколько это возможно. Фиксируется число нереализованных продаж.

4. Определяется, снизился ли запас до точки восстановления (в примере — 5 единиц). Если да, причем не ожидается поступле­ния заказа, сделанного ранее, то делается заказ.

Первый эксперимент Проводкова (объем заказа — 10 шт., точ­ка восстановления запаса — 5 шт.; СЧ — случайное число):

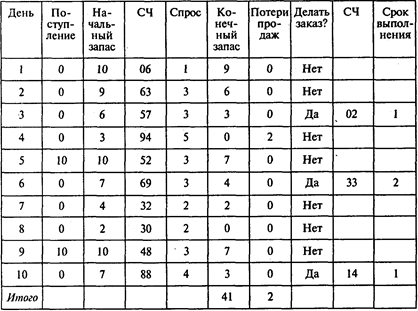
Результат имитационного эксперимента:

конечный суммарный запас — 41 единица;

средний конечный запас 41/10 =4,1 единицы;

число упущенных продаж — 2;

среднее число упущенных продаж 2/10 = 0,2 шт. в день;

среднее число заказов 3/10 = 0,3 заказа в день.

Определим три составляющие затрат:

Ежедневные затраты на заказы = Затраты на один заказ х Сред­нее число заказов в день = 10 • 0,3 = 3 руб.

Ежедневные затраты на хранение = Затраты на хранение одной единицы в течение дня х Средняя величина конечного за­паса = 5 • 4,1 = 20,5 руб.

Ежедневные упущенные продажи = Прибыль от упущенной продажи х Среднее число упущенных продаж в день = 80 • 0,2 = 16 руб.

Таким образом,

Общие ежедневные затраты = Затраты на заказы + Затраты на хранение + Упущенные продажи = 3 + 20,5 + 16 = 39,5 руб.