Приложения первообразной

Понятие криволинейной трапеции.

Пусть на отрезке [а,в] оси Ох задана непрерывная функция f, не меняющая на нём знака. Фигуру, ограниченную графиком этой функции, отрезком [а,в] и прямыми х = а и х = в называют криволинейной трапецией.

Приведём различные примеры криволинейных трапеций.

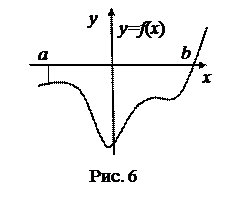
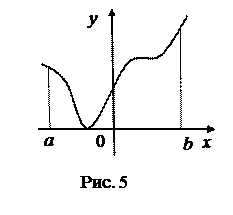
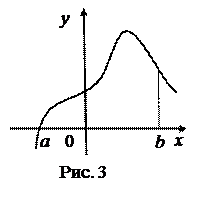
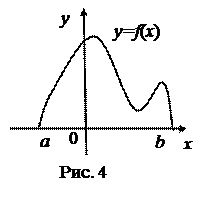
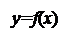
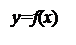
Полезно показать контрпримеры.

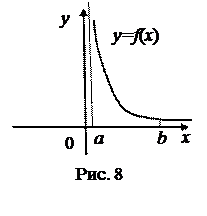
Теорема о площади криволинейной трапеции.

Если f – непрерывная и неотрицательная на отрезке [а,в] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [а,в], то есть S=F(a) - F(b).

Дано: функция f – непрерывна при ,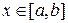

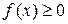при ,

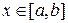F(x) – первообразная f на .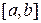

S – площадь соответствующей криволинейной трапеции.

Доказать: S=F(b) - F(a).

Доказательство

1. Зададим на отрезке [а,в] функцию S(x):

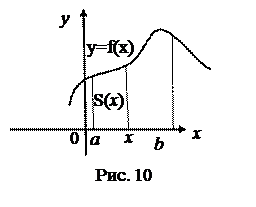если 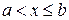, то S(х) – площадь той части криволинейной трапеции, которая расположена левее вертикальной прямой, проходящей через точку М (х;0);

если х = а, то S(a)=0.

2. Докажем, что S(x) – первообразная функции у = f(x) на [а,в], то есть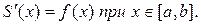

Напомним, что производная – это предел разностных отношений .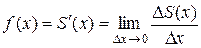

Выясним геометрический смысл числителя DS(x).

Пусть Dх > 0, DS(x)= S(x+Dx) - S(x).

Графически

Подменим криволинейную трапецию DS(x) равновеликим прямоугольником

со стороной х + Dх.

DS(x)=f(c)·Dx. :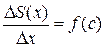

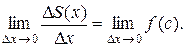
Найдем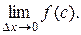

При 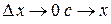. Поэтому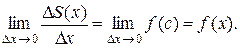

3. S(x)=F(x) + c.

При х = а S(a) = 0. c = - F(a). S = S(b), то есть S = F(b) - F(a).