Как превзойти алгоритм

К вопросу о том, как установить ис­тинность математических утверждений, мы вернемся позднее, в связи с теоремой Ге-деля (см. главу 4). Пока же я бы хотел обратить ваше внимание на то, что дока­зательство Тьюринга носит гораздо более

конструктивный характер и не столь негативно, как могло показаться из предыдущего изложения. Мы ведь не показали, что есть некая определенная машина Тьюринга, для которой абсолютно невозможно ре шить, останавливается она или нет. Более того, если внимательно проследить за доказательством, то выяснится, что для ка­жущихся «чрезвычайно сложными» машин j сама процедура Тьюринга, использованная i для их построения, неявным образом да- \ ет ответ\ Посмотрим, как это происходит. Допустим, у нас есть алгоритм, который иногда позволяет определить, что машина Тьюринга не остановится. Вышеописанная процедура Тьюринга позволяет явно просле­дить за вычислениями машины Тьюринга в случае, когда этот конкретный алгоритм не дает ответа на вопрос об остановке вы­числительного процесса. Однако тем самым эта процедура дает нам в этом случае воз­можность узнать ответ! Конкретная машина Тьюринга, за работой которой мы следим, и вправду никогда не остановится.

Чтобы подробно разобраться в этом во­просе, предположим, что у нас есть некий алгоритм, который иногда позволяет решить проблему остановки. Как и ранее, мы обо­значим этот алгоритм (машину Тьюринга) через Н, но теперь мы допускаем, что этот алгоритм не всегда может точно определить, что машина Тьюринга не остановится:

так что 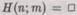возможно в случае,

когда 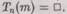Существует немало алгоритмов типа Н(п;т). (Например, Н(п;т) мог бы просто давать на выходе 1, как толь­ко машина Т_п(т) останавливается, хотя та­кой алгоритм едва ли представляет большой практический интерес!)

Мы можем повторить процедуру Тью­ринга, следуя уже пройденным путем, с той только разницей, что теперь некоторые из «» останутся не замененными на нули. Как и ранее, применив диагональный процесс, получим 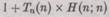в качестве n-го элемента диагонали. (Мы бу­дем иметь D каждый раз, когда 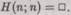Отметим, что .) Это безупречно алгоритмизованное вычисление, поэтому оно может быть произведено не­которой машиной Тьюринга, скажем k-й, и тогда мы получим

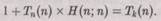
Для k-го диагонального элемента (т.е. n=k)

мы имеем

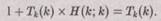
Если вычисления T_k(k) останавливаются, то мы приходим к противоречию (в этом случае Н(k; k) должно равняться единице, но тогда возникнет невыполнимое равен­ство: 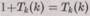). Значит, T_k(k) не мо­жет остановиться, т. е.

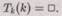
Но алгоритм не может этого «знать», потому что, если бы он давал H(k; k) = 0, мы снова пришли бы к противоречию (мы получи­ли бы тогда неверное соотношение 1 + 0=). Таким образом, если мы можем отыс­кать k, то мы знаем, как построить вы­числительную процедуру, для которой ал­горитм не дает решения проблемы оста­новки, но нам ответ известен! А как нам найти k? Это непростая задача. Необходи­мо тщательно изучить конструкцию Н(п; т) и Т_п(т) и понять, как в точности действует 1 + Т_n(п) х Н(п; п) в качестве машины Тью­ринга. Затем надо определить номер этой машины, который и есть k. Конечно, это выполнить трудно, но вполне возможно. Из-за этих трудностей вычисление T_k(k) нас бы вовсе не интересовало, не будь она специально предназначена для доказатель­ства неэффективности алгоритма Н! Важно то, что мы получили строго определенную процедуру, которая для любого наперед за­данного алгоритма Н позволяет найти та­кое k, что для T_k(k) этот алгоритм не мо­жет решить проблему остановки, т. е. мы тем самым превзошли его. Возможно, мысль о том, что мы «умнее» каких-то алгоритмов, принесет нам некоторое удовлетворение!

На самом деле, упомянутая процедура настолько хорошо определена, что мы мог­ли бы даже найти алгоритм для нахожде­ния k по заданному Н. Поэтому, прежде чем мы «погрязнем» в самодовольстве, мы должны осознать, что этот алгоритм мо­жет улучшить Н, поскольку он, по сути, «знает», что 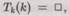— или все-таки нет? В предыдущем изложении было удоб­но использовать антропоморфный термин «знать» по отношению к алгоритму. Одна­ко не мы ли в конечном счете «знаем», тогда как алгоритм просто следует опреде­ленным нами правилам? А может быть мы сами просто следуем правилам, запрограм­мированным в конструкции нашего мозга и в окружающей нас среде? Эта проблема затрагивает не только алгоритмы, но и то, как мы выносим суждения об истинности и ложности. К этим важнейшим проблемам мы вернемся позднее. Вопрос о математиче­ской истине (и ее неалгоритмической при­роде) будет рассмотрен в главе 4. На данный момент мы, по крайней мере, получили не­которое представление о значении слов «ал­горитм» и «вычислимость» и достигли по­нимания некоторых из относящихся к ним вопросов.