ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

Пример: Рассмотрим последовательность 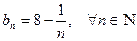. Последовательность имеет вид: 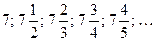. Таким образом, 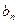с возрастанием номера n приближается к 8. Придадим этому утверждению точную математическую формулировку.

Зафиксируем число 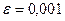и поставим вопрос, каким должно быть n, чтобы модуль 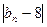был меньше 0,001?

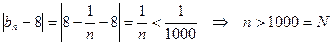
Для произвольного числа 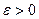неравенство

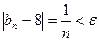(1)

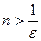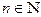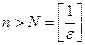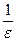равносильно неравенству . Так как , то неравенство (1) выполняется для всех , где – целая часть числа . В этом случае говорят, что предел последовательности равен 8 и пишут .

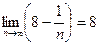Определение 1. Пусть задана числовая последовательность 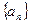. Число a называется пределом этой последовательности, если для каждого заданного числа 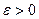найдётся такое натуральное число N, что для любого номера 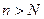выполняется неравенство .

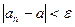В этом случае пишут .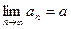

Иначе,

.

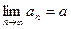
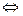
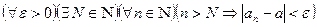Определение 2. Последовательность, имеющая предел, называется сходящейся, а не имеющая предела – расходящейся.

Теорема 1. Если последовательность имеет предел, то она ограничена.

Доказательство:

Пусть 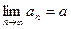. Зафиксируем некоторое 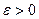, тогда

.

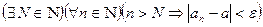Таким образом, 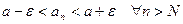. Вне интервала могут оказаться лишь N первых членов последовательности: . Среди чисел 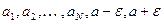найдём наименьшее и наибольшее и обозначим их соответственно m и M. Тогда 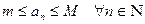. Отсюда последовательность 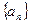ограничена.

Теорема 2. Всякая сходящаяся последовательность имеет только один предел.

Доказательство:

Используем метод от противного. Пусть последовательность 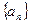имеет два различных предела a и b (для определённости ).

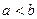Возьмём 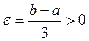, отсюда . Тогда справедливо неравенство:

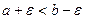. (2)

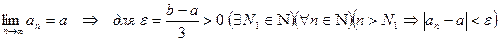
Отсюда , в частности, .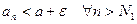

С другой стороны,

.

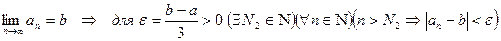Отсюда , в частности, .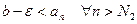

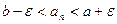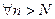Получаем для , где 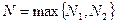, что противоречит неравенству (2). Теорема доказана.