Способ пропорциональных частей(метод хорд) для уточнения изолированного корня алгебраического или трансцендентного уравнения. Оценка погрешности.
Если уравнение достаточно сложно, то его очень редко удается решить точно, кроме того в уравнении могут быть коэффициенты которые получены экспериментально то есть являются приближенными сама задача о получении точного решения теряет смысл, по этому важное значение приобретает способы нахождения приближенного решения степень точности этого решения.
f(x)=0 (1), где f(x) – определена и непрерывна в некотором конечном интервале (a,b) или ( 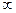 ) в дальнейшем потребуется существование и непрерывность первой производной f,(x) или f,,(x).
) в дальнейшем потребуется существование и непрерывность первой производной f,(x) или f,,(x).
Всякое значение 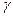 которая обобщает функцию в 0, называют корнем уравнения (1).
которая обобщает функцию в 0, называют корнем уравнения (1).
Будет представлять, что уравнение (1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность не содержащая других корней.
Приближенное нахождение изолированных корней (действительных) корней обычно состоит из 2-х этапов:
1. Определение корней, т.е. установление возможно тесных промежутков ( 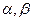 ) в которых существует только один корень.
) в которых существует только один корень.
2. Уточнение корней, доведение корней до требуемой степени точности f(x)=0 (1) для (1) этапа.
Т.1.
Если непрерывная f(x) принимает значение разных знаков на отрезке [ 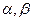 ], f(
], f( 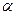 )*f(
)*f( 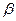 )<0 то внутри отрезка [
)<0 то внутри отрезка [ 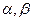 ] найдется хотя бы один корень т.е. Будет существовать
] найдется хотя бы один корень т.е. Будет существовать 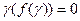
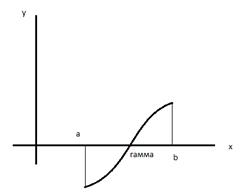
f,(x) существует и сохраняет при этом свой знак на отрезке [ 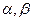 ].
].
Для определения корней часто бывает достаточно провести процесс половинного деления, примерно деля отрезок на 2,4,6 равных интервалов. И определение знака функции f(х) в точке деления.
Следует помнить, что алгебраическое уравнение n-й степени имеет не более n-корней.
Для оценки погрешности приближенного значения корня, справедлива теорема.
Т.2.
Пусть 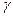 точный корень уравнения (1) а
точный корень уравнения (1) а 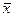 приближенный корень уравнения,
приближенный корень уравнения, 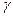 ,
, 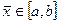 , причем
, причем 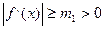 , тогда
, тогда 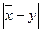 , абсолютная погрешность не превосходит значения
, абсолютная погрешность не превосходит значения 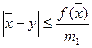 (2)
(2)
Доказательство:
Воспользуемся формулой Лагранжа
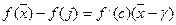
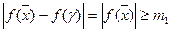 это модуль всегда ли-но
это модуль всегда ли-но 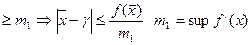
Графическое решение уравнения f(x)=0.
Действительные корни уравнения (1) можно определить как абцису точки пересечения с осью ох, но иногда удобней уравнение (1) привести к виду 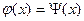 в этом случае искомые корни мы найдем через пересечение 2-х прямых.
в этом случае искомые корни мы найдем через пересечение 2-х прямых.
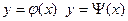
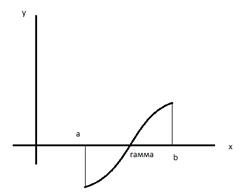
Метод хорд
f(x)=0 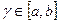 , произведение f(a)*f(b)<0. Разделим отрезок [a,b] -
, произведение f(a)*f(b)<0. Разделим отрезок [a,b] - 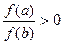 тогда x1=a+h1
тогда x1=a+h1
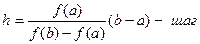
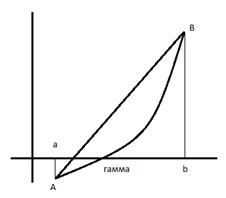
Точки A(a,f(x)) B(b,f(b)) следовательно 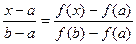
Положим f(x)=0, получим, что x=x1 следовательно 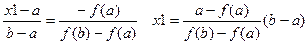 пусть вторая производная f(x)>0
пусть вторая производная f(x)>0
Рассмотрим
1. f(a)<0
2. f(a)>0
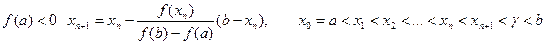
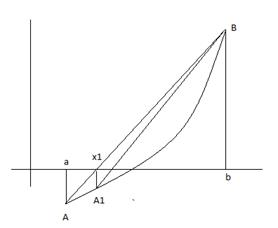

Данная последовательность приближений ограничена сверху и возрастает, следовательно существует предел последовательности 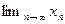
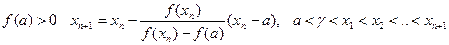
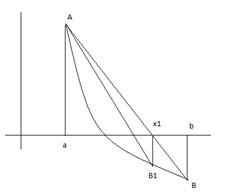
Данная последовательность приближений ограничена снизу и убывает, следовательно существует предел последовательности 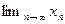
Обобщим:
1. Неподвижным является тот конец отрезка для которого знак функции совпадает со знаком второй производной f(x), а последовательное приближение лежит по ту сторону корня, где функция имеет знак противоположный знаку 2-й производной.
В любом случае каждое следующее значение xn ближе к 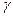 , поэтому как только
, поэтому как только 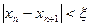 (Е- предельная абсолютная погрешность), (0<E<1),то это гарантирует что
(Е- предельная абсолютная погрешность), (0<E<1),то это гарантирует что 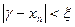
2. Для оценки точности приближения можно воспользоваться 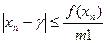
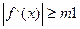 m1- наименьшее значение
m1- наименьшее значение 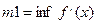 на [a,b] наименьшее значение
на [a,b] наименьшее значение
f(x)=0 (1).
Дата добавления: 2022-05-27; просмотров: 102;










