Процессы наращения и дисконтирования в финансовых операциях.
1.1 Процентная ставка
Простейшие и самые распространенные финансовые операции связаны с кредитом. Если вы хотите занять деньги, то идете в банк. Банк даст вам деньги с определенными условиями возврата, которые включают величину, способы возврата и время возврата денег. Если вы предоставляете свой капитал на определенное время, то тоже указываете в договоре величину, способы возврата и время возврата денег. При заключении финансового договора кредитор и заемщик договариваются о величине процентной ставки. Процентная ставка (rate of interest) является одной из основных характеристик кредитных, финансовых, коммерческих и инвестиционных контрактов. Процентная ставка – одно из основных финансовых понятий.
 Процентная ставка учитывает фактор времени. В контрактах обязательно указывается сроки, периоды выплаты денег.
Процентная ставка учитывает фактор времени. В контрактах обязательно указывается сроки, периоды выплаты денег.
Фраза «доллар сегодня дороже, чем доллар завтра», отражает основной принцип неравноценности денег, относящихся к разным моментам времени (time-value of mоny). Имеющуюся сегодня сумму можно инвестировать и получить в будущем доход, и сегодняшние 1000 руб. имеют большую ценность, чем те же 1000 руб. через три или пять лет с учетом инфляции и рисков невозврата инвестиции (кредита). Фактор времени в долгосрочных операциях иногда оказывается важнее, чем величина суммы денег.
Процентная ставка учитывает временной интервал, который называется периодом начисления (running period). Периодом начисления может быть год, квартал, месяц, день. В практической деятельности и в финансовой статистике обычно подразумеваются годовые процентные ставки.
Процентная ставка учитывает риски финансовых операций и инфляцию. Процентная ставка является мерой эффективности (доходности) финансовой деятельности, кредитования, инвестиции, коммерческой деятельности.
Существуют различные типы процентных ставок. Ставки наращения (interest base rate): простые, сложные и непрерывные. Учетные ставки (discount rate). Процентные ставки бывают фиксированным и плавающими. Базовая процентная ставка показывает изменяющуюся во времени базу и размер надбавки к ней (маржу). Например, межбанковская ставка LIBOR[1] (London interbank offered rate), базовая ставка по рублевым кредитам МИБОР.
Важные для финансовой деятельности процентные ставки имеют специальное название. Это ставки рефинансирования Центрального Банка России (для США Федеральной резервной системы, далее ФРС). Ставка рефинансирования – это процентная ставка, по которой ЦБ выдает кредиты коммерческим банкам. За их изменениями внимательно следят участники финансового рынка.
Процентные ставки изменяются во времени, и зависимость от времени процентной ставки (временная структура процентной ставки) является одной их важнейших характеристик финансового рынка. Информация о процентных ставках публикуется на сайтах государственных финансовых институтов (ЦБ), специальных информационных агентств, фондовых бирж.
Процентные ставки обычно выражаются процентах. Однако далее везде в формулах для удобства вычислений будем использовать процентные ставки в виде десятичной дроби.
Таблица процентных ставок (interest rate)
| Country | Canada | Denmark | Hungary | Iceland | Japan | Korea | United Kingdom | United States | Brazil | China | India | Russian Federation | South Africa |
| 4,25 | 3,69 | 7,98 | 16,15 | 0,26 | 4,50 | 5,08 | 5,24 | 19,98 | 3,33 | 6,00 | 11,00 | 9,00 | |
| 4,26 | 4,24 | 7,01 | 14,04 | 0,50 | 4,99 | 5,60 | 4,24 | 17,85 | 3,33 | 6,00 | 10,00 | 11,00 | |
| 1,50 | 4,40 | 10,12 | 18,25 | 0,21 | 3,27 | 1,65 | 0,16 | .. | .. | 6,00 | 13,00 | 11,50 |
1.2 Процессы наращения и дисконтирования.
Процесс наращения – это увеличение первоначальной суммы денег. Пусть 
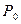 - исходная сумма,
- исходная сумма, 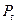 - наращенная сумма за время t или будущая сумма . Эффективность такой финансовой операции за один период Т от t = 0 до t = T рассчитывается как доля прироста капитала к первоначальной сумме
- наращенная сумма за время t или будущая сумма . Эффективность такой финансовой операции за один период Т от t = 0 до t = T рассчитывается как доля прироста капитала к первоначальной сумме
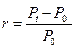 . (1.1)
. (1.1)
Величина 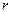 называется процентной ставкой за период наращения Т.
называется процентной ставкой за период наращения Т.
Рис.1.1 Графическое изображение процесса наращения.
Настоящее. Будущее.
Начальная (настоящая) сумма Возвращаемая (будущая)сумма
(РV-present value)[2] (FV –future value)
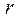
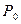
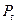
наращение
Наращенная сумма за период t, как следует из формулы (1.1) равна
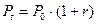 . (1.2)
. (1.2)
Время генерирует деньги.
Если известна возвращаемая сумма 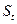 и надо найти отношение прироста к конечной сумме
и надо найти отношение прироста к конечной сумме 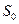 , то этот процесс называется дисконтированием.
, то этот процесс называется дисконтированием.
Рис.1.2 Графическое изображение процесса дисконтирования.
Настоящее. Будущее.
Начальная (настоящая) сумма Возвращаемая (будущая)сумма
(РV-present value) (FV –future value)
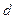

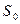
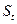
дисконтирование
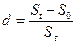 , (1.3)
, (1.3)
Величина d – называется ставкой дисконтированияза время t. Дисконтом D называется разница между суммой возврата 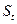 и первоначальной суммой долга.
и первоначальной суммой долга.
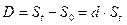 . (1.4)
. (1.4)
Величина 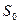 из (1.3) равна
из (1.3) равна
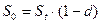 . (1.5)
. (1.5)
В финансовой практике d называется учетной ставкой. Учетная ставка используется тогда, когда плата за кредит (процентный доход) начисляется авансом при выдаче кредита. Заемщику выдается сумма, уменьшенная на величину процентного дохода, а возвращается полная сумма долга.
Из формул (1.2) и (1.5) легко найти связь между процентной ставкой 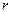 и учетной ставкой
и учетной ставкой 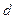 .
.
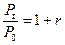 ,
, 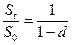 . Если
. Если 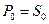 , а
, а 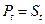 , то
, то 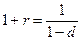 ,
,
следовательно процентная ставка 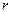 и дисконт
и дисконт 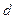 cвязаны соотношением
cвязаны соотношением
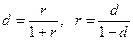 . (1.6)
. (1.6)
Из приведенных формул следует, что теоретическая дисконтная ставка 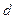 меньше процентной ставки
меньше процентной ставки 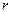 .
.
Наряду с банковским дисконтированием, в котором используется учетная ставка, применяется и математическое дисконтирование, в котором, используется процентная ставка 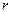 . При математическом дисконтировании сумма за один период равна
. При математическом дисконтировании сумма за один период равна
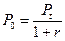 . (1.7)
. (1.7)
Если величина 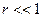 , то можно использовать приближение
, то можно использовать приближение 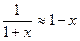 , в результате получим
, в результате получим 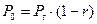 .
.
Выше приведенные соотношения между начальной и наращенной суммой соответствуют одному временному интервалу – периоду начисления (дисконтирования) 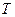 . Если таких периодов несколько, то в формулах наращения (1.2) и дисконтирования (1.5) появляется коэффициенты (множители) наращения и дисконтирования.
. Если таких периодов несколько, то в формулах наращения (1.2) и дисконтирования (1.5) появляется коэффициенты (множители) наращения и дисконтирования.
Пример 1. Фирма получила кредит на один год в размере 10 млн. руб. с условием возврата: а) 15млн. руб., б) 10,5 млн. руб. Найти процентную ставку и дисконт.
Пример 2. Кредит был выдан под 12% годовых. Найти начальную сумму, если возвращаемая сумма равна 650 тыс. руб.
Пример 3. Сравнить наращенные проценты по процентной ставке и учетной ставке, считая их равными.
1.3. Начисление простого процента и сложного процента.
Простой процент.
Простой процент начисляется за все время действия контракта на определенную первоначальную сумму. Этот способ начисления процентов называют “наращением без капитализации”. Наращенная сумма при ежегодном начислении процентов или будущая стоимость (future value) равна
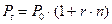 , (1.8)
, (1.8)
где r – годовая процентная ставка n – число лет.
Если начисление процента происходит ежедневно, то для простых процентов наращенная сумма рассчитывается по формуле
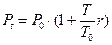 , (1.9)
, (1.9)
где 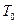 - временная база, или число дней в финансовом году[3], Т – число дней наращения.
- временная база, или число дней в финансовом году[3], Т – число дней наращения.
Процентный доход равен 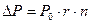 или
или 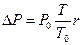 .
.
Пример 4. Кредит в размере 2 млн. руб. был выдан на 60 дней под 12% годовых. Найти наращенную сумму и процентный доход.
Пример 5. Банк предлагает депозит с начислением на первоначальную сумму. Первые три месяца по ставке 4% годовых, в следующие три месяца процентная ставка увеличивается на 0,5%. Найти наращенную сумму и процентный доход, если сумма вклада составляет 30 000руб.
Сложный процент.
Начисление сложного процента осуществляется на наращенную сумму, поэтому этот способ начисления называют «наращением с капитализацией». Наращенная сумма при начислении сложного процента за произвольное число дней 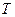 равна
равна
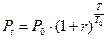 , (1.10)
, (1.10)
где r - годовая процентная ставка, выраженная в виде долей единицы. Величина 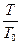 часто бывает нецелым числом. Иногда для расчета наращенной суммы при дробном числе лет применяться приближенная формула.
часто бывает нецелым числом. Иногда для расчета наращенной суммы при дробном числе лет применяться приближенная формула.
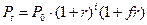 , (1.11)
, (1.11)
где i- целая часть числа 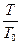 , а f - дробная часть этого числа. Если начисление сложных процентов происходит m раз в году течении n лет, то расчет наращенной суммы за время
, а f - дробная часть этого числа. Если начисление сложных процентов происходит m раз в году течении n лет, то расчет наращенной суммы за время 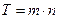 производят по формуле
производят по формуле
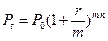 , (1.12)
, (1.12)
где r – годовая процентная ставка (номинальная), 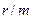 – процентная ставка за период (periodic interest rate). Величина
– процентная ставка за период (periodic interest rate). Величина 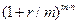 – называется множителем наращения, а
– называется множителем наращения, а 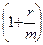 – коэффициентом наращения.
– коэффициентом наращения.
Наращенная сумма зависит от частоты начисления процентов. Чем больше частота начисления процентов, тем больше наращенная сумма. Таким образом, для вкладчика выгоднее частое начисление процентов, а для заемщика наоборот. В кредитных контрактах и депозитных договорах, когда начисление процентов происходит по сложной процентной ставке, указывается годовая процентная ставка, которая называется номинальной.
Непрерывное начисление процентов.
Если частота начисления процентов становится непрерывной, то есть частота начисления процентов бесконечно возрастает 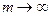 , а временной интервал начисления становится бесконечно малым, то наращенная сумма или будущая стоимость рассчитывается по формуле
, а временной интервал начисления становится бесконечно малым, то наращенная сумма или будущая стоимость рассчитывается по формуле
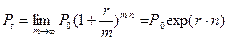 , (1.13)
, (1.13)
где 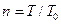 – число лет. При выводе (1.13) использовалось известное приближение
– число лет. При выводе (1.13) использовалось известное приближение 
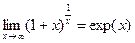 , где
, где 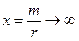 , при
, при 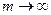 .
.
В практике кредитных расчетов непрерывное начисление процентов применяется редко. Обычно для кредитных расчетов применяется ежедневное начисление процентов. При непрерывном начислении процентов наращенная сумма рассчитывается по формуле
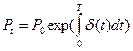 , (1.14)
, (1.14)
где – 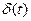 сила роста, которая является фактически непрерывной процентной ставкой. Если сила роста постоянна, то наращенная сумма за время T равна
сила роста, которая является фактически непрерывной процентной ставкой. Если сила роста постоянна, то наращенная сумма за время T равна
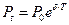 , (1.15)
, (1.15)
Если величина 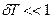 , то используя приближение
, то используя приближение 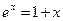 , получим
, получим 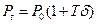 .
.
При нестабильной экономике процентные ставки могут значительно изменяться в течение года. В этом случае наращенная сумма вычисляется по формуле
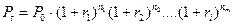 , (1.16)
, (1.16)
где 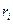 – последовательные значения процентных ставок в соответствующие периоды
– последовательные значения процентных ставок в соответствующие периоды 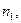 ..
.. 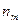 .
.
Если необходимо найти количество лет для увеличения начальной суммы в N раз, то для простых процентов из формулы (1.8) получим
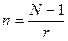 ; (1.17)
; (1.17)
для сложных процентов из формулы (1.12) получим
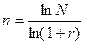 , (1.18)
, (1.18)
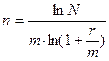 . (1.19)
. (1.19)
Пример 6. Сколько лет потребуется для увеличения первоначальной суммы в 1,2 раза, если номинальная процентная ставка равна 9%, а начисление процентов происходит 4 раза в год.
Решение. По формуле (1.19) найдем необходимое число лет:
N = 1,2; m = 4, 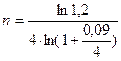
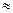 2 года.
2 года.
Пример 7. Рассчитать накопленную сумму для различных вариантов начисления процентов за один год, два года, 5 лет. Начальная сумма равна 1000 руб., годовая процентная ставка равна 10%.
Решение. Расчет проведем по формуле (1.12) в Excel. Результаты расчетов приведены ниже в таблице и на гистограммах ниже.
Таблица 1.1. Наращенные суммы и множители наращения для различной частоты начисления процентов в году.
| сумма | Частота начислений в году | Наращенная сумма | Базисное наращение | Цепное наращение |
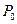
| m | 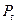
| 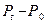
| 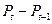
|
Начальная сумма 1000

| ||||
| 1102,5 | 102,5 | 2,5 | ||
| 1103,813 | 103,813 | 1,313 | ||
| 1104,260 | 104,260 | 0,448 | ||
| 1104,713 | 104,713 | 0,453 | ||
| 1105,171 | 105,171 | 0,458 |
| частота начисления % | m | Множитель наращения | ||
| один год | два года | пять лет | ||
| раз в год | 1,1 | 1,21 | 1,61051 | |
| два раза в год | 1,1025 | 1,2155 | 1,6289 | |
| раз в квартал | 1,1038 | 1,2184 | 1,6386 | |
| шесть раз в году | 1,1043 | 1,2194 | 1,6419 | |
| ежемесячно | 1,1047 | 1,2204 | 1,6453 | |
| ежедневно | 1,1052 | 1,2214 | 1,6486 | |
| непрерывное | 1,1052 | 1,2214 | 1,6487 |
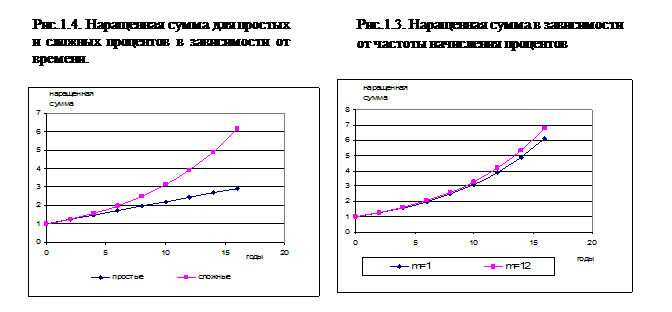
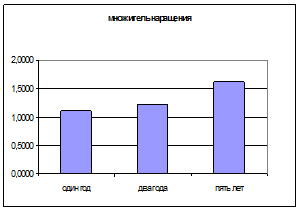
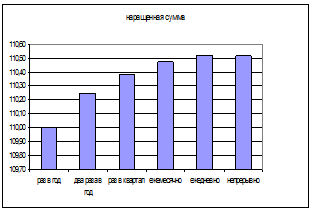
Из приведенных выше расчетов и графика (рис.1.5) видно, что чем больше частота начисления процентов за тот же период начисления 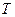 , тем больше наращенная сумма. Причем цепное наращение
, тем больше наращенная сумма. Причем цепное наращение 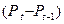 , начиная с частоты равной 6 раз в год, растет практически на постоянную величину
, начиная с частоты равной 6 раз в год, растет практически на постоянную величину 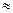 0,45. Эта динамика замедления роста наращенной суммы с ростом частоты начисления процентов видна и на рис. 1.5. Увеличение наращенной суммы с ростом числа лет (периода начисления) не замедляется, поскольку как видно из формулы (1.12)
0,45. Эта динамика замедления роста наращенной суммы с ростом частоты начисления процентов видна и на рис. 1.5. Увеличение наращенной суммы с ростом числа лет (периода начисления) не замедляется, поскольку как видно из формулы (1.12) 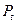 и рисунка является степенной функцией числа лет
и рисунка является степенной функцией числа лет 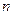 .
.
Рис. 1.5. Зависимость наращенной суммы и величины множителя наращения от частоты начисления процентов.
Эффективная процентная ставка.
 В финансовых расчетах при анализе доходности финансовых операций часто приходится сравнивать различные виды процентных ставок, в которых выражается доходность данной конкретной финансовой операции. Например, банки предоставляют различные виды депозита с различными сроками, частотой начисления процентного дохода, различными номинальными ставками. Какой вариант выбрать? Или, например, вы хотите инвестировать 100000 руб. Возможны несколько вариантов: положить на депозит, купить облигации или купить акции. Эти финансовые операции также характеризуются величиной процентной ставки. Для сравнения результатов финансовых операций обычно применятся эффективная процентная ставка.
В финансовых расчетах при анализе доходности финансовых операций часто приходится сравнивать различные виды процентных ставок, в которых выражается доходность данной конкретной финансовой операции. Например, банки предоставляют различные виды депозита с различными сроками, частотой начисления процентного дохода, различными номинальными ставками. Какой вариант выбрать? Или, например, вы хотите инвестировать 100000 руб. Возможны несколько вариантов: положить на депозит, купить облигации или купить акции. Эти финансовые операции также характеризуются величиной процентной ставки. Для сравнения результатов финансовых операций обычно применятся эффективная процентная ставка.
Эффективная процентная ставка численно равна годичной ставке сложных процентов, дающей то же соотношение между полученной суммой 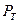 за время t = T и затраченной суммой
за время t = T и затраченной суммой 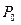 , которая получается при любой схеме выплат.
, которая получается при любой схеме выплат.
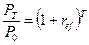 , (1.20)
, (1.20)
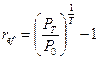 , (1.21)
, (1.21)
где Т измеряется в годах. Эффективная процентная ставка, как видно из формулы (1.21), зависит от отношения конечной и начальной сумм 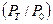 и от продолжительности периода начисления процентов
и от продолжительности периода начисления процентов 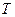 .
.
Если проценты начисляются m раз в год по схеме сложных процентов, то формула (1.20) приобретает более простой вид. Действительно, из формулы (1.12), учитывая, что Т = n получим
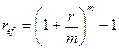 . (1.22)
. (1.22)
Эффективная процентная ставка позволяет сравнить доходности различных финансовых операций или, другими словами, сравнить различные методы получения процентного дохода.
Пример 8. Найти эффективную процентную ставку при ежеквартальном начислении сложных процентов. Номинальная (годовая) процентная ставка равна 18%.
Пример 9. Предприниматель может получить ссуду в размере 100 тыс. руб.: а) на условиях ежеквартального начисления сложных процентов из расчета 75% годовых, б) на условиях полугодового начисления сложных процентов из расчета 80% годовых. Какой вариант предпочесть?
. 1. 4. Процентная ставка в условиях инфляции.
Если имеется инфляция, то для сохранения заданной доходности (реальной доходности) расчеты следует проводить по процентной ставке учитывающей инфляцию[4].
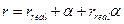 , (1.23)
, (1.23)
 где r – номинальная процентная ставка,
где r – номинальная процентная ставка, 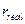 – реальная процентная ставка,
– реальная процентная ставка, 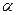 – темп инфляции. Иногда номинальную ставку называют брутто-ставкой. Формулу (1.22) называют формулой Фишера, вывод которой приведен ниже. Обычно в популярной литературе считают, что для сохранения заданной доходности (
– темп инфляции. Иногда номинальную ставку называют брутто-ставкой. Формулу (1.22) называют формулой Фишера, вывод которой приведен ниже. Обычно в популярной литературе считают, что для сохранения заданной доходности ( 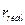 ) достаточно чтобы номинальная ставка превышала реальную доходность на величину темпа инфляции, но это верно для малых величин
) достаточно чтобы номинальная ставка превышала реальную доходность на величину темпа инфляции, но это верно для малых величин 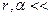 0,2.
0,2.
С темпом инфляции связан индекс цен за период T
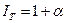 . (1.24)
. (1.24)
Если необходимо вычислить инфляцию за большой период 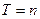 , а она не является постоянной, то инфляция
, а она не является постоянной, то инфляция 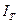 равна
равна
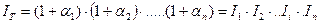 , (1.25)
, (1.25)
где 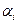 - темп инфляции за соответствующий временной период,
- темп инфляции за соответствующий временной период, 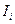 – индекс цен соответствующий i – му моменту времени. Если в течении n периодов инфляция постоянна, то темп инфляции
– индекс цен соответствующий i – му моменту времени. Если в течении n периодов инфляция постоянна, то темп инфляции 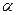 связан с индексом I соотношением
связан с индексом I соотношением 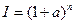 .
.
Вывод формулы Фишера.
Пусть 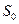 - стоимость товара в начале периода,
- стоимость товара в начале периода, 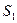 - стоимость товара, например, через год. Темп инфляции равен
- стоимость товара, например, через год. Темп инфляции равен
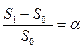 . (1.26)
. (1.26)
Очевидно, что из-за инфляции на ту же сумму денег товаров можно купить меньше. Реальная стоимость денег при инфляции уменьшается. Для того, чтобы купить такое же количество товара нужна сумма 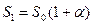 . Пусть имеется сумма
. Пусть имеется сумма 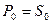 . Если текущая процентная ставка равна r, то через год вы получите сумму равную
. Если текущая процентная ставка равна r, то через год вы получите сумму равную 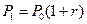 . Чтобы деньги сохранили свою покупательную способность необходимо, чтобы наращенная сумма
. Чтобы деньги сохранили свою покупательную способность необходимо, чтобы наращенная сумма 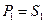 , или
, или
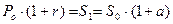 . (1.27)
. (1.27)
Если, кроме избегания инфляции, надо получить доход, то 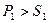 . Пусть эта сумма равна
. Пусть эта сумма равна 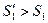 . Реальная процентная равна
. Реальная процентная равна
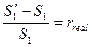 . (1.28)
. (1.28)
Из (1.28) 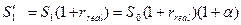 после подстановки
после подстановки 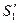 в (1.27) вместо
в (1.27) вместо 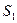 получим
получим
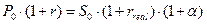 .
.
Если 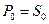 , то процентная ставка равна
, то процентная ставка равна
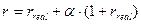 . (1.29)
. (1.29)
Такая процентная ставка обеспечивает реальную эффективность финансовой операции.
Реальная процентная ставка из (1.29) равна
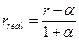 . (1.30)
. (1.30)
Если темп инфляции превышает номинальную ставку 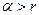 , то реальная процентная ставка становится отрицательной. Это означает, что наращенная сумма не компенсирует потерю покупательной способности денег из-за инфляции.
, то реальная процентная ставка становится отрицательной. Это означает, что наращенная сумма не компенсирует потерю покупательной способности денег из-за инфляции.
Полученная зависимость процентной ставки от темпа инфляции, может быть проверена статистическими методами, например, с помощью построения регрессионной модели. Такая проверка была проведена[5]. Предсказанная линейная зависимость подтвердилась для долгосрочных процентных ставок на срок более пяти лет. Для краткосрочных процентных ставок такая линейная зависимость не подтверждается.
Пример 10. Кредит 12,0 млн. руб. был выдан на 3 года. На этот период прогнозируется рост цен в 2,2 раза. Определить ставку процента при выдаче кредита и наращенную сумму долга, если реальная доходность этой финансовой операции для кредитора должна составлять 12% годовых.
1.5. Дисконтирование и наращение по процентной и учетной ставкам.
Часто при выдаче кредита необходимо найти первоначальную сумму 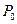 при известной конечной сумме
при известной конечной сумме 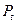 . В зависимости от типа процентной ставки используют два типа дисконтирования. Дисконтирование по процентной ставке
. В зависимости от типа процентной ставки используют два типа дисконтирования. Дисконтирование по процентной ставке 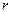 называется математическим дисконтированием, а дисконтирование по учетной ставке
называется математическим дисконтированием, а дисконтирование по учетной ставке 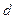 называется банковским дисконтированием. Для того, чтобы различать формулы для банковского и математического дисконтирования или наращения, далее будем использовать следующие обозначения:
называется банковским дисконтированием. Для того, чтобы различать формулы для банковского и математического дисконтирования или наращения, далее будем использовать следующие обозначения:
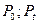 - начальная и наращенная сумма по процентной ставке
- начальная и наращенная сумма по процентной ставке 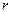 ;
;
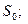
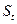 -начальная и наращенная сумма по учетной ставке
-начальная и наращенная сумма по учетной ставке 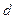 .
.
Математическое дисконтирование.
Начальная сумма 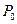 , которая выдается в кредит, находится из формул наращения для простых и сложных процентов (1.8-1.9) и (1.10; 1.12):
, которая выдается в кредит, находится из формул наращения для простых и сложных процентов (1.8-1.9) и (1.10; 1.12):
для простых процентов 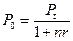 , (1.31)
, (1.31)
для сложных процентов с начислением процентов m раз в году 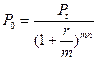 , (1.32)
, (1.32)
для непрерывных процентов 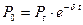 . (1.33)
. (1.33)
Сумма 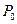 - это начальная сумма, а
- это начальная сумма, а 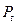 - наращенная (будущая) сумма. Индекс t обозначает временной интервал, для которого рассчитывается наращенная сумма. Например, при ежегодном начислении простых процентов в течении n лет t = n.
- наращенная (будущая) сумма. Индекс t обозначает временной интервал, для которого рассчитывается наращенная сумма. Например, при ежегодном начислении простых процентов в течении n лет t = n.
Банковское дисконтирование.
При банковском[6] дисконтировании, так же как и при математическом дисконтировании, требуется найти начальную сумму 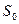 , выданную в кредит при известной сумме погашения кредита
, выданную в кредит при известной сумме погашения кредита 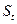 через период t. Процентный доход за кредит выплачивается сразу при выдаче суммы кредита, которая меньше на величину наращенных процентов, рассчитанных по учетной ставке d. Рассмотрим виды банковского дисконтирования.
через период t. Процентный доход за кредит выплачивается сразу при выдаче суммы кредита, которая меньше на величину наращенных процентов, рассчитанных по учетной ставке d. Рассмотрим виды банковского дисконтирования.
Дисконтирование по простой учетной ставке. Учет векселя
При простой ставке дисконтирования d за n периодов дисконтирования начальная сумма 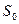 равна
равна
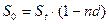 . (1.34)
. (1.34)
Дисконтирование по простой учетной ставке применяется для краткосрочных кредитов. Коммерческий кредит – это предоставление товаров и услуг с оплатой через определенное время. Условия оплаты кредита весьма разнообразны. Распространенным инструментом коммерческого кредита является коммерческий вексель.[7] Процедура учета векселя (дисконтирования) заключается в продаже его векселедержателем банку или другому субъекту по цене ниже номинальной стоимости векселя. Сумма, выдаваемая банком держателю векселя при учете по простой учетной ставке d за 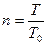 периодов дисконтирования равна
периодов дисконтирования равна
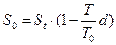 , (1.35)
, (1.35)
где 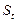 - номинал векселя, или сумма, которую должен получить векселедержатель при его погашении через время Т – число дней, оставшееся до погашения векселя, d –учетная ставка или величина дисконта ( процента), по которой банк или другое лицо приобрело вексель у векселедержателя до срока его погашения,
- номинал векселя, или сумма, которую должен получить векселедержатель при его погашении через время Т – число дней, оставшееся до погашения векселя, d –учетная ставка или величина дисконта ( процента), по которой банк или другое лицо приобрело вексель у векселедержателя до срока его погашения, 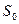 – сумма, которую получит векселедержатель при досрочном погашении,
– сумма, которую получит векселедержатель при досрочном погашении, 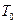 – временная база обычно равная 360 дней. Учетная ставка должна учитывать риски, связанные с погашением векселя. Дисконт при учете векселя равен
– временная база обычно равная 360 дней. Учетная ставка должна учитывать риски, связанные с погашением векселя. Дисконт при учете векселя равен 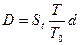 .
.
Дисконтирование по сложной учетной ставке.
При дисконтировании по сложной учетной 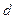 ставке начальная сумма равна
ставке начальная сумма равна
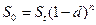 , (1.36)
, (1.36)
где 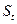 – сумма в конце n-го периода, d – учетная ставка за период,
– сумма в конце n-го периода, d – учетная ставка за период, 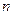 – число периодов дисконтирования. Если дисконтирование проводится m раз в год, то дисконтированная сумма равна
– число периодов дисконтирования. Если дисконтирование проводится m раз в год, то дисконтированная сумма равна
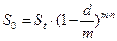 , (1.37)
, (1.37)
где d – годовая учетная ставка, которая называется номинальной учетной ставкой.
При непрерывном дисконтировании по учетной ставке дисконтированная сумма равна
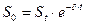 . (1.38)
. (1.38)
Пример 11. Фирма продала товар на условиях коммерческого кредита с оформлением простого векселя номинальной стоимостью 2,5 млн. руб., сроком 60 дней. Через 45 дней фирма решила учесть вексель в банке. Предложенная банком учетная ставка равна 12%. Найти сумму, полученную векселедержателем и дисконт.
Решение. При учете векселя банком владелец векселя получит сумму (1.34) равную

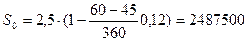 руб.
руб.
Дисконт равен 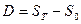 ; или
; или 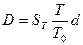 ;
; 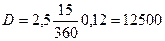 руб.
руб.
Существуют другие способы учета векселей, например, по методу математического дисконтирования (1.31). Владелец векселя в этом случае получит сумму равную 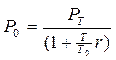 =
= 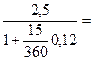 2487562 руб.
2487562 руб.
Дисконт равен 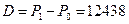 руб. Как видно, при учете векселя по методу математического дисконтирования величина дисконта меньше. В зависимости от условий кредитования возможны различные варианты учета векселей.
руб. Как видно, при учете векселя по методу математического дисконтирования величина дисконта меньше. В зависимости от условий кредитования возможны различные варианты учета векселей.
Наращение по учетной ставке.
Наращенная сумма по учетной ставке d легко находится из формул дисконтирования для учетной ставке (1.35.-1.37). Наращенная сумма 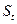
для простой учетной ставки равна 
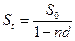 , (1.39)
, (1.39)
для сложной учетной ставки с начислением m раз в году 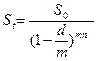 . (1.40)
. (1.40)
Для операций наращения важным является также момент начисления процентов. Начисление процентов возможно в начале периода или в конце периода. Подробнее эти методы описаны в гл.2. Декурсивный (последующий) метод – начисление процентов происходит в конце расчетного периода. При этом наращенная сумма рассчитывается по процентной ставке r по формулам (1.8-1.13). Антисипативный (предварительный) метод – начисление процентов происходит в начале расчетного периода на сумму, которую следует вернуть, наращенная сумма рассчитывается по учетной ставке d (1.39; 1.40).
Пример 12. Срочный вклад в размере 800 тыс. руб. положен в банк на 2,5 года. На вклад начисляются сложные проценты по учетной ставке d = 15% годовых. Рассчитать наращенную сумму по двум методам а) декурсивному 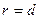 , б) антисипативному.
, б) антисипативному.
Решение. Наращенная сумма по декурсивному методу находится по формуле (1.35)
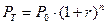 =
= 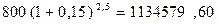 руб.
руб.
Наращенная сумма по антисипативному методу находится по формуле (1.39)
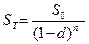 =
= 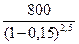 =1201тыс. руб.
=1201тыс. руб.
Как видно, при антисипативном способе начисления процентов наращенная сумма больше.
1.6. Эквивалентность процентных ставок
Процентные и учетные ставки в кредитных операциях решают одну и ту же задачу: определяют величину наращенной или дисконтированной суммы. Очевидно, что можно выбрать такие значения и виды процентных и учетных ставок, при которых результаты финансовых операций будут равноценны. Равноценность финансовых результатов означает, что равны начальные, конечные суммы и сроки кредитов.
 Процентные ставки, обеспечивающие равноценность финансовых результатов, называются эквивалентными или релятивными (относительными). Эквивалентные процентные ставки означают, что безразлично, по какой процентной ставке получается данная конечная сумма. Соотношение эквивалентности для процентных ставок легко получается из условия равенства отношения наращенной суммы к начальной сумме, т.е. равенства дисконтных множителей или множителей наращения.
Процентные ставки, обеспечивающие равноценность финансовых результатов, называются эквивалентными или релятивными (относительными). Эквивалентные процентные ставки означают, что безразлично, по какой процентной ставке получается данная конечная сумма. Соотношение эквивалентности для процентных ставок легко получается из условия равенства отношения наращенной суммы к начальной сумме, т.е. равенства дисконтных множителей или множителей наращения.
Соотношения эквивалентности простой процентной ставки и учетной ставки получается из формул (1.2) и (1.5)
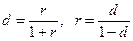 . (1.41)
. (1.41)
Соотношения эквивалентности простой и сложной номинальной ставок легко получить, приравнивая дисконтные множители. При начислении сложных процентов дисконтный множитель за весь период равен 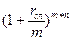 ; для простых процентов дисконтный множитель равен
; для простых процентов дисконтный множитель равен 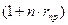 . Приравнивая выражения в правых частей формул, получим процентную ставку сложных процентов эквивалентную ставке простых процентов
. Приравнивая выражения в правых частей формул, получим процентную ставку сложных процентов эквивалентную ставке простых процентов
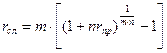 . (1.42)
. (1.42)
Процентная ставка простых процентов эквивалентная сложной процентной ставке равна
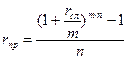 . (1.43)
. (1.43)
Пример 13. Ссуда выдана на 1,5 года под 25% простых годовых процентов. Найти эквивалентную ставку сложных процентов при начислении процентов раз (два) в год.
Пример 14. Какой годовой ставке простых процентов соответствует годовая ставка сложных процентов 20%, если начисление по ней производится ежеквартально?
Эквивалентность простой учетной и номинальной процентной ставок
Соотношения эквивалентности простой учетной и номинальной сложной процентной ставки получим, приравнивая дисконтные множители простой учетной (1.35) и сложной процентной (1.12) ставок. В результате получим, что номинальная ставка эквивалентная простой учетной равна
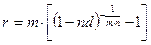 , (1.44)
, (1.44)
а простая учетная ставка эквивалентная номинальной равна
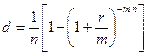 , (1.45)
, (1.45)
где 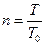 . Используя эквивалентность процентных ставок, можно показать, что метод непрерывного начисления процентов содержит в себе все выше рассмотренные способы начисления процента.
. Используя эквивалентность процентных ставок, можно показать, что метод непрерывного начисления процентов содержит в себе все выше рассмотренные способы начисления процента.
Пример 15. Банк выдал ссуду на 1 год и 3 мес. под 20% годовых сложных процентов с ежемесячным начислением. Найти величину простой учетной ставки, при которой банк получил такую же наращенную сумму.
Упражнение. Оформите таблицу самостоятельно, заполнив пропущенные клетки в таблице
| Таблица 1.2. Таблица эквивалентности процентных ставок. | |||||||
| Вид ставки | Простой процент r | Простая учетная ставка d | Cложный процент m=1
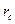
| Cложный процент m раз в год
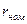
| Эффективная ставка | Сложная учетная ставка 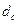
| Непрерывная ставка 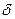
|
| Простой процент r = | 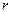
| 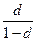
| 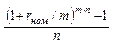
| 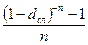
| |||
| Простая учетная ставка d= | 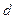
| 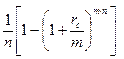
| 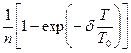
| ||||
Cложный процент m=1
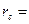
| 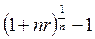
| 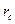
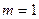
| 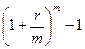
| 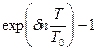
| |||
Cложный процент m раз в год 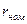
| 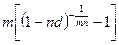
| 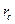
| |||||
Эффективная ставка
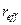 = =
|  
Дата добавления: 2021-11-16; просмотров: 320; |











