В идеально-упругой среде.

Основной задачей в дальнейшем будет рассмотрение взаимосвязей между напряжениями и деформациями, а также теми структурными изменениями в твердых телах, к которым приводят те или иные деформации. Строгого математического описания этих взаимосвязей в настоящее время не существует вследствие сложности процессов , происходящих в телах при их нагружении. Поэтому при теоретическом исследовании деформирования и разрушения твердых тел прибегают к различным идеализациям.

Любое тело, подвергающееся действию внешних сил, испытывает деформации. Каждому типу напряженного состояния соответствует определенная деформация. Если напряжения относительно невелики, то деформированное тело принимает после снятия нагрузки первоначальную форму и размеры, т.е. полностью возвращается в исходное. Это свойство тел называется абсолютной упругостью.

Если после снятия нагрузки начальная форма восстанавливается не полностью, то вводится понятие остаточной деформации. При дальнейшем повышении нагрузки происходят более сложные явления в твердых телах, которые будут нами рассмотрены позже.

Тело может считаться абсолютно упругим до достижения некоторого критического значения деформации, за которым начинается или пластическое состояние или начало трещинообразования.

Напряжение, при котором достигается это критическое состояние, называется пределом упругости материала.

В теории упругости, принимается, что материал обладает свойством сплошности, однородности и изотропности.

Сплошной материал – пренебрегается дискретностью строения реальных тел.

Однородное тело – свойства одинаковы по всему объему.

Изотропность – упругие свойства тел в точке не зависят от направления.

Такие допущения с успехом применяются при исследовании напряженного состояния в реальных грунтах при построении приближенного поля напряженности.

Фактически все эти условия и допущения строго не выполняются – существуют трещины, направленность зерен и кристаллов. Тем не менее, размеры неоднородностей, разрывы сплошности и анизотропия в ряде случаев являются несущественным для феноменологического описания поля напряжений и деформаций.

Зависимость между деформацией и приложенной силой в упругом теле впервые была сформулирована Гуком: “удлинение пропорционально силе” – в этом случае подразумевается удлинение стержня под действием растягивающей силы

,

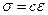где c – постоянная,

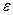- продольная деформация

В случае объемного напряженного состояния рассматриваются напряжения и деформации вдоль главных направлений. В этом случае напряжения называются главными напряжениями, а деформации – главными деформациями.

Если линии 1,2,3 являются главными направлениями деформации, то касательные напряжения вдоль них равны нулю, то – есть, это одновременно и направления главных напряжений.

Для объемного тела в любой точке сплошной среды каждый из шести компонентов напряжений является линейной функцией шести компонентов деформаций и наоборот. Для главных направлений обобщенный закон Гука принимает вид:

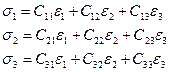(3)

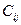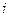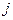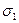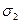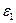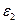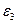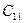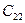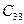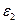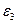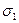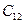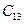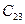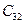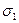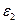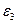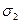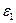Коэффициент является упругой постоянной, связывающей напряжение в направлении c деформациями в направлениях . Для изотропного тела влияние напряжений , , на величину деформации , , одинаково, потому = = . Из того же условия изотропности следует, что удлинения и при действии напряжения одинаковы, откуда = . Аналогично этому = и = . 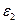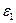Кроме того, влияние на или должно быть таким же, как и влияние на или , и влияние на или .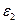

Поэтому

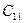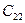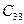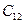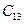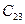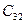= = , = = = = = (3.4)

Из равенства (3.4) следует, что относя деформацию к главным осям, остается только две упругие постоянные, которые обозначим через a и b. Тогда уравнения примут вид:

(3.5)

Принимая a-b=2 и b= и пользуясь обозначением e= 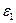+ + 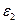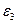(объемная деформация) перепишем (5) в виде:

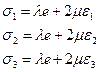(3.6)

где 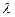, - постоянные Ламе

Для произвольных направлений можно получить:

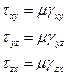
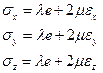(3.7)

Соотношения (3.7) представляют собой простейшее уравнение состояния среды, для характеристики свойств которой введены две постоянные: 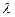и .

Связь между деформациями и напряжениями можно представить также в виде:

(3.8)

Упругая деформация обратима, т.е. кривые деформируемости при разгрузке и сжатии одинаковы, поэтому он называется просто модулем упругости, обозначается через E. Он носит также название модуля Юнга:

(3.9)

Удлинение или укорочение элемента объема материала в направлении x сопровождается сужением или расширением в перпендикулярном направлении, что выражается соотношением:

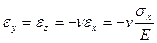(3.10)

где - коэффициент Пуассона

Согласно обобщенному закону Гука (3.8) для рассматриваемого случая одноосного сжатия имеем

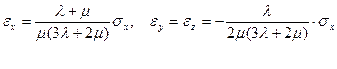(3.11)

Из сравнения(3.9),(3.10) и (3.11) следует

(3.12)

Отношение компонента касательного напряжения к соответствующему компоненту

деформации сдвига называется модулем упругости при сдвиге (модуль сдвига) и обозначается через G:

(3.13)

Из (7) и (13) следует 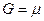. Решая (3.12) относительно , получим

,

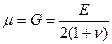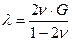
Таким образом, все используемые в механике упругие постоянные могут быть выражены через и и наоборот. .Обобщенный закон Гука можно представить с использованием упругих постоянных в виде

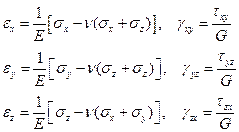(3.14)

Эти же уравнения выраженные через компоненты деформации, имеют вид:

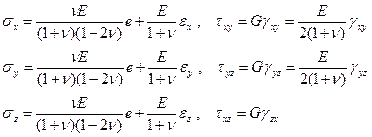(3.15)