Числовые характеристики дискретного случайного процесса.
Математическое ожидание Мx, дисперсия Dx, среднеквадратическое отклонение σξ и коэффициент корреляции ρxh .
Математическое ожидание.
Определение. Математическое ожидание Мx случайной величины x определяется формулой
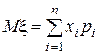
и фактически есть «её среднее значение». Это легко видеть из Таблиц 1 и 2.
Важно отметить, что Мx — математический оператор.
Задача 3. Найти математическое ожидание случайной величины, заданной законом распределения
| x | -1 | |
| pi | 1/3 | 2/3 |
Mx = -1·1/3 +×1·2/3 = 1/3.
Свойства математического ожидания.
1. Если случайная величина x постоянна, т. е. x º С, то её математическое ожидание равно С: М(С) = С.
2. Если Мx = а, и k – константа, то М(kx) = kа, т.е.математическое ожидание случайной величины, умноженной на число, равно математическому ожиданию случайной величины, умноженному на это число.
3. Если Мx=а, и k и b– константы, то М(kx+b) = kа+b, т.е. математическое ожидание суммы случайной величины и числа равно сумме этого числа и математического ожидания случайной величины.
4. Для любых двух случайных величин x и h, определённых на одном и том же пространстве элементарных исходов, справедлива формула: М(x+h) = М(x)+М(h).
5. Если случайные величины x и h независимы, то М(x·h) = Мx×Мh.
Покажем это на примере.
Задача 4.
Заданы законы распределения двух независимых случайных величин x и h
| x | h | -2 | |||||
| pi | 1/2 | 1/2 | pi | 1/3 | 2/3 |
М(x) = 1·1/2+0·1/2 = 1/2,
М(h) = (-2)·1/3+3·2/3 = 4/3. Тогда М(x)·М(h) = 2/3.
Построим закон распределения для случайной величины y = x·h
| y | -2 | |||
| pi | 1/6 | 1/6 | 2/6 | 2/6 |
Упорядочим значения случайной величины по возрастанию
| y | -2 | ||
| pi | 1/6 | 3/6 | 2/6 |
М(y) = М(x·h) = (-2)·1/6+0·3/6+3·2/6 = 2/3.
Среднее значение случайной величины даёт ориентировочное представление о случайной величине, и во многих случаях этого достаточно.
Однако, одного математического ожидания недостаточно. Почему? Вот пример.
| x | -0,01 | 0,01 | h | -100 | ||||
| pi | 1/2 | 1/2 | pi | 1/2 | 1/2 |
М(x) = -0,01·1/2+0,01·1/2 = 0
М(h) = (-100)·1/2+100·1/2 = 0.
Поэтому вводят ещё одну величину, характеризующую колеблемость, как средний квадрат отклонения значения случайной величины от её среднего значения.
Дата добавления: 2021-11-16; просмотров: 79;










