Подпоследовательностей
1.Число  является пределомпоследовательности
является пределомпоследовательности
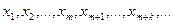 (5.1.)
(5.1.)
тогда и только тогда, когда  — предел подпоследовательности
— предел подпоследовательности
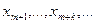 . (5.2)
. (5.2)
Необходимость.Пусть 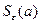 — произвольная окрестность точки
— произвольная окрестность точки  . Так как
. Так как  — пределпоследовательности (5.1), то из условия 3 теоремы 2.5 следует, что вне окрестности
— пределпоследовательности (5.1), то из условия 3 теоремы 2.5 следует, что вне окрестности 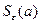 находится лишь конечное число членов последовательности (5.1). По условию теоремы только
находится лишь конечное число членов последовательности (5.1). По условию теоремы только 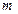 элементов последовательности (5.2) не принадлежит последовательности (5.1). Следовательно, вне окрестности
элементов последовательности (5.2) не принадлежит последовательности (5.1). Следовательно, вне окрестности 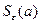 находится лишь конечное число членов последовательности (5.2). Теперь из условия 3 теоремы 2.5 следует, что число
находится лишь конечное число членов последовательности (5.2). Теперь из условия 3 теоремы 2.5 следует, что число  является пределомпоследовательности (5.2).
является пределомпоследовательности (5.2).
Достаточность доказывается аналогично. ■
Замечание.Из утверждения 1 следует, чтопри нахождении предела последовательности можно «отбросить» любое конечное число ее членов. ▲
2.Если предел последовательности  равен
равен  , то предел любой ее подпоследовательности
, то предел любой ее подпоследовательности 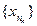 также равен
также равен  .
.
Доказательство. Пусть 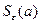 — произвольная окрестность точки
— произвольная окрестность точки  . Так как
. Так как  — пределпоследовательности
— пределпоследовательности  , то из условия 3 теоремы 2.5 следует, что вне окрестности
, то из условия 3 теоремы 2.5 следует, что вне окрестности 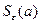 находится лишь конечное число ее членов. Подпоследовательность
находится лишь конечное число ее членов. Подпоследовательность 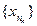 является частью последовательности
является частью последовательности  , поэтому вне окрестности
, поэтому вне окрестности 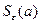 находится лишь конечное число членов подпоследовательности
находится лишь конечное число членов подпоследовательности 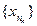 . Теперь из теоремы 2.5 следует, что
. Теперь из теоремы 2.5 следует, что 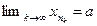 . ■
. ■
Следствие. Последовательность  расходится, если выполняется хотя бы одно из следующих условий.
расходится, если выполняется хотя бы одно из следующих условий.
а) Последовательность  содержит две подпоследовательности, которые сходятся к разным пределам.
содержит две подпоследовательности, которые сходятся к разным пределам.
б) Последовательность  содержит расходящуюся подпоследовательность.
содержит расходящуюся подпоследовательность.
Доказательстволегко получается методом от противного. Если предположить, что последовательность  сходится, то сейчас же вступаем в противоречие с утверждением 2. ■
сходится, то сейчас же вступаем в противоречие с утверждением 2. ■
3.Если последовательность  есть объединение двух своих подпоследовательностей
есть объединение двух своих подпоследовательностей 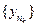 и
и 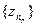 , причем
, причем 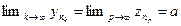 , то
, то 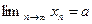 .
.
Доказательство.Пусть число 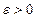 . Так как
. Так как 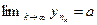 , то из условия 3 теоремы 2.5 вне окрестности
, то из условия 3 теоремы 2.5 вне окрестности 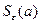 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности 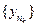 . Ввиду
. Ввиду 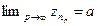 и условия 3 теоремы 2.5 следует, что вне окрестности
и условия 3 теоремы 2.5 следует, что вне окрестности 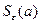 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности 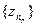 .
.
По условию теоремы 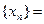
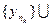
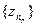 . Значит, вне окрестности
. Значит, вне окрестности 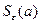 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности  , поэтому условие 3 теоремы 2.5 выполняется. Отсюда вытекает, что
, поэтому условие 3 теоремы 2.5 выполняется. Отсюда вытекает, что 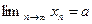 . ■
. ■
Примеры
5.1. Доказать, что 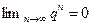 , если
, если 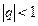 .
.
Решение. Возьмем произвольное число 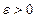 . Имеем следующую цепочку равносильных утверждений:
. Имеем следующую цепочку равносильных утверждений:
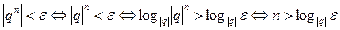 .
.
Теперь из второго утверждения теоремы 2.1 и второго утверждения теоремы 2.5 следует, что 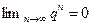 .
.
5.2. Доказать расходимость последовательности  :
:
a) 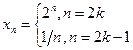 ; б)
; б) 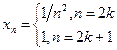 .
.
Решение
а)Последовательность  содержит неограниченную подпоследовательность
содержит неограниченную подпоследовательность 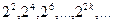 , которая расходится. Из второго утверждения следствия к свойству 3 следует, что последовательность
, которая расходится. Из второго утверждения следствия к свойству 3 следует, что последовательность  расходится.
расходится.
б) Последовательность  содержит подпоследовательность
содержит подпоследовательность
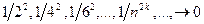 .
.
Кроме того,последовательность  содержит стационарную подпоследовательность
содержит стационарную подпоследовательность
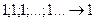 .
.
Итак, последовательность  содержит две подпоследовательности, которые сходятся к разным пределам. Из первого утверждения следствия к свойству 3 следует, что последовательность
содержит две подпоследовательности, которые сходятся к разным пределам. Из первого утверждения следствия к свойству 3 следует, что последовательность  расходится.
расходится.
5.3. Найти предел последовательности 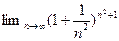 .
.
Решение. Последовательность 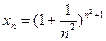 является подпоследовательностью последовательности
является подпоследовательностью последовательности 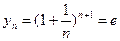 , так как
, так как 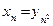 . Из 3-го утверждения в § 2.5 и
. Из 3-го утверждения в § 2.5 и 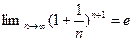 следует, что
следует, что 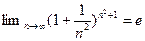 .
.
5.4. Найти предел последовательности
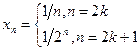 .
.
Решение. Данная последовательность является объединением двух подпоследовательностей, состоящих из четных и нечетных членов. Предел каждой из этих подпоследовательностей равен нулю. Из свойства 4 вытекает, что предел последовательности равен нулю.
5.5. Доказать, используя второе утверждение теоремы 2.5, что 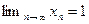 , если
, если 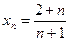 .
.
Решение. При любом 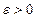 имеем цепочку равносильных утверждений:
имеем цепочку равносильных утверждений:
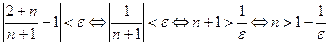 .
.
Теперь из второго утверждения теоремы 2.1 и второго утверждения теоремы 2.5 следует, что 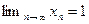 .
.
Замечание. Далее необходимо помнить следующие пределы
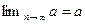 ,
, 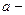 число;
число; 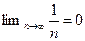 ;
; 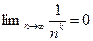 , если
, если 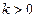 ;
;
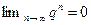 , если
, если 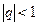 ;
; 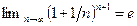 . ▲
. ▲
Задачи
5.1. Доказать, используя второе утверждение теоремы 2.5, что 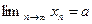 :
:
a) 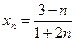 ,
, 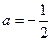 ; б)
; б) 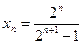 ,
, 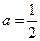 ; в)
; в) 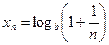 ,
, 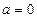 .
.
5.2. Найти предел последовательности 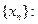
а) 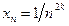 ; б)
; б) 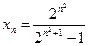 ; в)
; в) 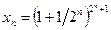 ; г)
; г) 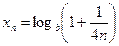 ,
, 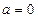 .
.
5.3. Доказать расходимость последовательности 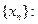
а) 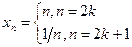 ; б)
; б) 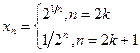 .
.
5.4. Доказать, что монотонная последовательность сходится, если сходится какая-нибудь ее подпоследовательность.
§2.6. Действия со сходящимися последовательностями
Теорема 2.6. Если последовательности  и
и 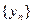 имеют предел, то последовательность
имеют предел, то последовательность 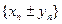 имеет предел и
имеет предел и
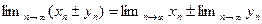 .
.
Доказательство.Пусть 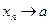 ,
, 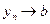 и произвольное
и произвольное 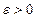 задано. Далее имеем:
задано. Далее имеем: 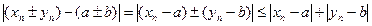 .
.
Согласно условию 2 теоремы 2.5 неравенство 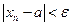 справедливо при всех
справедливо при всех 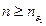 , а неравенство
, а неравенство 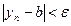 справедливо при всех
справедливо при всех 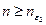 . Обозначим через
. Обозначим через 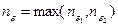 . Тогда при всех
. Тогда при всех  неравенство
неравенство
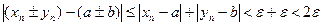
справедливо. Отсюда и из замечания к теореме 2.5 следует, что 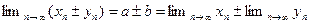 . ■
. ■
Пример
6.1. Найти предел последовательности 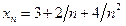 .
.
Решение. Используя теорему 2.6, имеем:
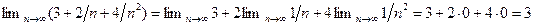 . ●
. ●
6.2. Найти предел последовательности 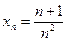 .
.
Решение. По теореме 2.6 имеем:
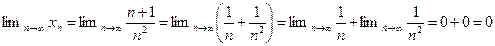 .●
.●
Теорема 2.7.Если последовательности  и
и 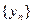 имеют предел, то последовательность
имеют предел, то последовательность 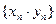 имеет предел и
имеет предел и
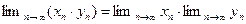 .
.
Доказательство. Пусть 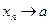 ,
, 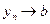 и произвольное
и произвольное 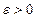 задано. Так как последовательность
задано. Так как последовательность 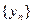 имеет предел, то она ограничена, поэтому
имеет предел, то она ограничена, поэтому 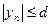 при любом
при любом 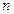 . Далее имеем:
. Далее имеем:
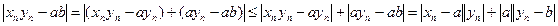 .
.
Согласно теореме 2.5 неравенство 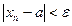 справедливо при всех
справедливо при всех  , а неравенство
, а неравенство 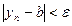 справедливо при всех
справедливо при всех 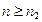 . Если
. Если 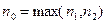 , то при всех
, то при всех 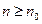 имеем:
имеем:
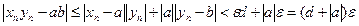 .
.
Из замечания к теореме 2.5 следует, что 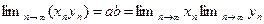 . ■
. ■
Следствие1.Если последовательность  имеет предел и
имеет предел и 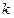 — число, то последовательность
— число, то последовательность 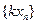 имеет предел и
имеет предел и 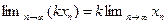 .
.
Доказательство. Последовательность 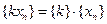 , где
, где 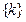 — стационарная последовательность. Теперь утверждение следствия вытекает из теоремы 2.7. ■
— стационарная последовательность. Теперь утверждение следствия вытекает из теоремы 2.7. ■
Следствие 2. Если последовательность  имеет предел, то
имеет предел, то
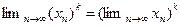 .
.
Доказательство. Имеем следующую цепочку равенств: 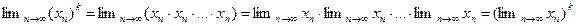 .■
.■
Теорема 2.8. Если последовательность 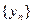 имеет предел, равный
имеет предел, равный 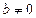 , то
, то 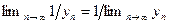 .
.
Доказательство. 1.Из следствия к теореме 7: если 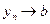 , то
, то 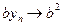 . Из условия
. Из условия 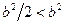 и следствия к теореме 5 получаем:
и следствия к теореме 5 получаем: 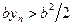
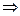
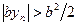 при всех
при всех  . Тогда при всех
. Тогда при всех  верно
верно 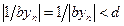 , где
, где 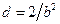 .
.
Теперь имеем цепочку: 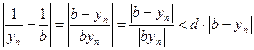 .
.
Так как по условию 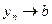 , то согласно условию 2 теоремы 5 неравенство
, то согласно условию 2 теоремы 5 неравенство 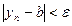 справедливо при всех
справедливо при всех 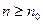 . Теперь при всех
. Теперь при всех 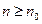 имеем:
имеем:
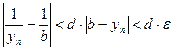 .
.
Из замечания к теореме 2.5 следует, что 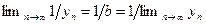 . ■
. ■
Теорема 2.9.Если последовательности  и
и 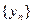 имеют предел и
имеют предел и 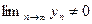 , то последовательность
, то последовательность 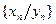 имеет предел и
имеет предел и
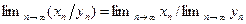 .
.
Доказательство.Используя теоремы 2.7 и 2.8, имеем:
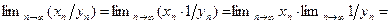
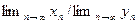 . ■
. ■
Замечание 1. При вычислении предела суммы, произведения или частного двух последовательностей очень часто нельзя сразу применить теоремы 2.6, 2.7 или 2.9, потому что слагаемые, сомножители или числитель и знаменатель дроби, не имеют предела. В этом случае надо так тождественными преобразованиями изменить сумму, произведение или частное, чтобы получилось выражение, к которому уже можно было бы применить теоремы 2.6, 2.7 или 2.9. ▲
Замечание 2. 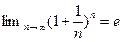 .
.
Так как предел последовательности 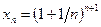 равен
равен 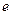 , и
, и
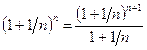 ,
, 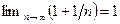 ,
,
то из теоремы 2.10 следует равенство 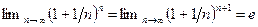 .▲
.▲
Примеры
6.3. Найти предел последовательности: a) 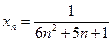 , б)
, б) 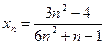 .
.
Решение. Применяя теоремы 2.6— 2.9, найдем:
а) 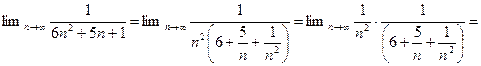
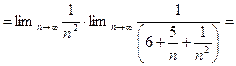
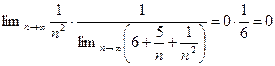 .
.
б) 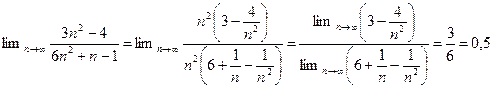 .
.
в) 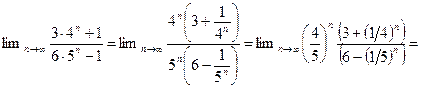
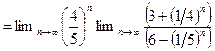
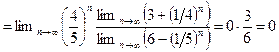 .
.
6.4. Доказать расходимость последовательности 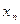 :
:
a) 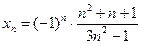 ; б)
; б) 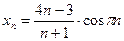 .
.
Решение
а) Подпоследовательность
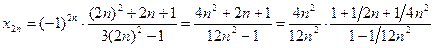
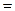
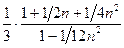 .
.
Отсюда, применяя теоремы 2.6-2.9: 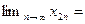
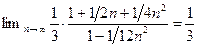 .
.
Подпоследовательность
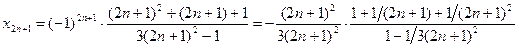
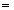
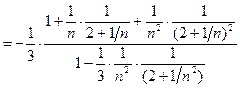 . Отсюда, применяя теоремы 2.6-2.9:
. Отсюда, применяя теоремы 2.6-2.9:
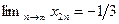 . Две подпоследовательности сходятся к разным пределам. Следовательно, последовательность не имеет предела.
. Две подпоследовательности сходятся к разным пределам. Следовательно, последовательность не имеет предела.
б) Подпоследовательность 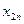 имеет предел:
имеет предел:
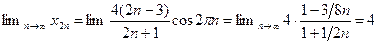 .
.
Подпоследовательность 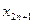 имеет предел:
имеет предел:
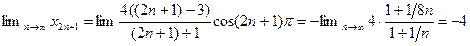 .
.
Две подпоследовательности сходятся к разным пределам. Следовательно, последовательность не имеет предела. ●
Задачи
6.1. Найти предел последовательности  :
:
a) 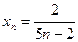 ; б)
; б) 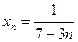 ; в)
; в) 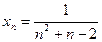 ; г)
; г) 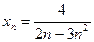 ; д)
; д) 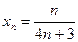 ;
;
е) 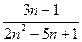 , ж)
, ж) 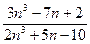 , з)
, з) 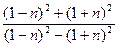 , и)
, и) 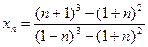 .
.
6.2. Найти предел последовательности  :
:
а) 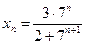 ; б)
; б) 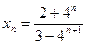 ; в)
; в) 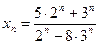 ; г) т.
; г) т.
6.3. Дано, 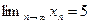 . Найти: а)
. Найти: а) 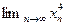 ; б)
; б) 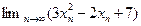 .
.
6.4. Доказать расходимость последовательности 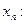
а) 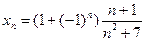 ; б)
; б) 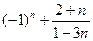 .
.
6.5. Последовательность 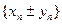 не имеет предела, если одна из последовательностей имеет предел, а другая последовательность не имеет предела.
не имеет предела, если одна из последовательностей имеет предел, а другая последовательность не имеет предела.
§ 2.7.Предельный переход в неравенстве
Теорема 2.10. Справедливы следующие утверждения.
1. Если последовательности  имеет предел и для всех
имеет предел и для всех 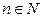 справедливо неравенство
справедливо неравенство 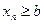
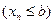 , то
, то 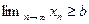
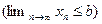 .
.
2.Если последовательности  и
и 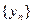 имеют предел и для всех
имеют предел и для всех 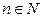 справедливо неравенство
справедливо неравенство 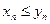 , то
, то 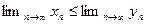 .
.
Доказательство. 1.Пусть 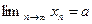 . Надо доказать, что
. Надо доказать, что 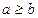 . Предположим, что
. Предположим, что 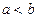 . Тогда из следствия к теореме 2.5 следует, что неравенство
. Тогда из следствия к теореме 2.5 следует, что неравенство 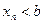 будет выполняться для всех
будет выполняться для всех 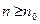 , что противоречит условию теоремы. Случай
, что противоречит условию теоремы. Случай 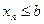 рассматривается аналогично.
рассматривается аналогично.
2.Из теоремы 2.6 вытекает, что предел последовательности 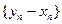 существует и ее члены
существует и ее члены 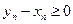 . Из 1-го утверждения теоремы 2.9 следует, что
. Из 1-го утверждения теоремы 2.9 следует, что 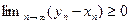 , поэтому
, поэтому 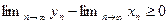 , т.е.
, т.е. 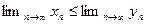 . ■
. ■
Теорема 2.11.(О трех последовательностях). Последовательности  ,
, 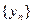 ,и
,и 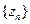 удовлетворяют условиям:
удовлетворяют условиям:
1. 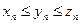 при любом
при любом 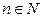 ; 2.
; 2. 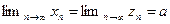 .
.
Тогда 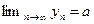 .
.
Доказательство.Пусть 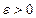 — произвольное число. Так как
— произвольное число. Так как 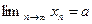 , и
, и 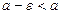 , то из следствия к теореме 2.5 следует, что
, то из следствия к теореме 2.5 следует, что 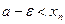 при всех
при всех  . Из условий
. Из условий 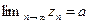 ,
, 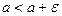 и следствия к теореме 2.5 вытекает, что
и следствия к теореме 2.5 вытекает, что 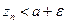 при всех
при всех 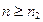 . Если
. Если 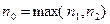 , то при всех
, то при всех 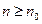 справедливо неравенство
справедливо неравенство 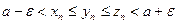 , поэтому при всех
, поэтому при всех 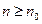 справедливо неравенство
справедливо неравенство 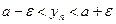 . Теперь из теоремы 2.5 следует, что
. Теперь из теоремы 2.5 следует, что 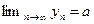 . ■
. ■
§ 2.8. Предел последовательности 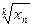
Теорема 2.12. Если предел последовательности  равен
равен 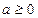 , и члены последовательности
, и члены последовательности 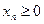 неотрицательны, то
неотрицательны, то
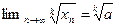 .
.
Доказательство. Сначала рассмотрим случай, когда 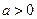 .Возьмем произвольное число
.Возьмем произвольное число 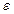 ,
, 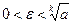 , и рассмотрим цепочку равносильных неравенств:
, и рассмотрим цепочку равносильных неравенств: 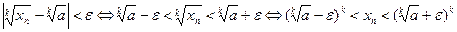 .
.
Так как 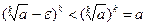 , то из следствия к теореме 2.5 следует, что неравенство
, то из следствия к теореме 2.5 следует, что неравенство 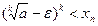 справедливо при всех
справедливо при всех 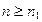 . Из следствия к теореме 2.5 и неравенства
. Из следствия к теореме 2.5 и неравенства 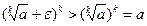 получаем, что неравенство
получаем, что неравенство 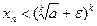 справедливо при всех
справедливо при всех 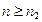 . Теперь неравенство
. Теперь неравенство
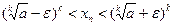
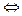
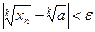
верно при всех 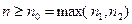 . Из второго утверждения теоремы 2.5 следует, что
. Из второго утверждения теоремы 2.5 следует, что 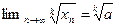 .
.
Пусть теперь 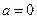 .Возьмем
.Возьмем 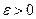 и рассмотрим цепочку равносильных неравенств:
и рассмотрим цепочку равносильных неравенств: 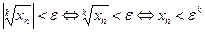 . Отсюда и из второго утверждения теоремы 2.5 следует, что неравенство
. Отсюда и из второго утверждения теоремы 2.5 следует, что неравенство 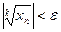 справедливо при всех
справедливо при всех 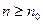 , т.е.
, т.е. 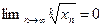 . ■
. ■
Замечание. Если предел последовательности  равен
равен 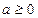 , и члены последовательности
, и члены последовательности 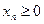 неотрицательны, то
неотрицательны, то
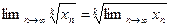 .
.
Доказательство. 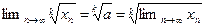 .
.
Следствие. Справедливы утверждения:
а) Если 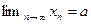 , то
, то 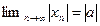 ; б)
; б)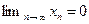
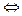
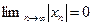 .
.
Доказательство.
а) 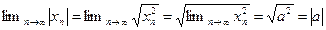 ;
;
б) При любом 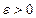 имеем следующую цепочку равносильных утверждений:
имеем следующую цепочку равносильных утверждений: 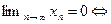
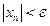 , если
, если 
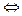
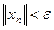 , если
, если 
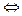
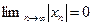 .
.
Пример. 8.1.Вычислить предел последовательности 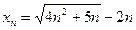 .
.
Решение. Сначала преобразуем общий член последовательности, умножая числитель и знаменатель на выражение 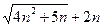 , а затем перейдем к вычислению предела, используя теорему 2.12:
, а затем перейдем к вычислению предела, используя теорему 2.12:
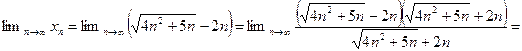
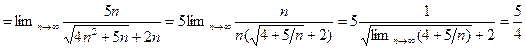 . ●
. ●
Задачи
8.1. Найти предел последовательности 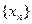 :
:
а) 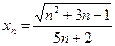 ; б)
; б) 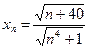 ; в)
; в) 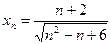 ; г)
; г) 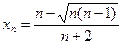 ;
;
д) 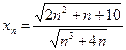 ; е)
; е) 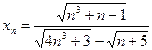 ; ж)
; ж) 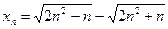 ;
;
з) 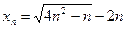 ; и)
; и) 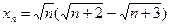 ; к)
; к) 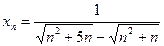 .
.
8.2. Доказать, что если предел последовательности 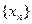 равен
равен 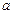 , то
, то
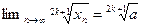 .
.
§2.9. Бесконечно малые и бесконечно большие последовательности
Бесконечно малые последовательности
Последовательность 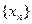 называется бесконечно малой, если ее предел равен нулю, т.е.
называется бесконечно малой, если ее предел равен нулю, т.е. 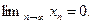 Среди бесконечно малых последовательностей отметим последовательности:
Среди бесконечно малых последовательностей отметим последовательности: 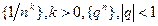 .
.
Свойства бесконечно малых последовательностей
1.Если последовательность 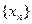 бесконечно малая, а последовательность
бесконечно малая, а последовательность 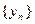 является ограниченной, то
является ограниченной, то 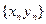 является бесконечно малой последовательностью.
является бесконечно малой последовательностью.
Доказательство.Из ограниченности последовательности 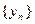 следует, что
следует, что 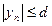 при всех
при всех 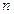 . Возьмем любое
. Возьмем любое 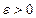 . Поскольку
. Поскольку 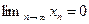 , то неравенство
, то неравенство 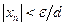 справедливо для всех
справедливо для всех 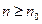 . Теперь неравенство
. Теперь неравенство 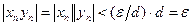 справедливо для всех
справедливо для всех 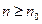 , т.е. выполняется условие 2 теоремы 2.5. Значит
, т.е. выполняется условие 2 теоремы 2.5. Значит 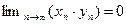 .
.
2. 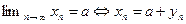 , где
, где 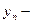 бесконечно малая последовательность.
бесконечно малая последовательность.
Доказательство. 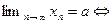
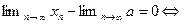
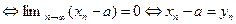 ,
, 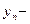 бесконечно малая
бесконечно малая 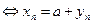 . ■
. ■
Примеры
9.1. Найти предел последовательности 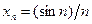 .
.
Решение. Так как 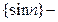 ограниченная последовательность, а
ограниченная последовательность, а 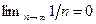 , то из первого свойства бесконечно малых последовательностей следует, что
, то из первого свойства бесконечно малых последовательностей следует, что
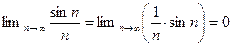 . ●
. ●
Теорема 2.13.Если 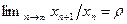 ,
, 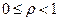 , и члены последовательности
, и члены последовательности 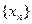 положительны, то
положительны, то 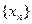 — бесконечно малая последовательность.
— бесконечно малая последовательность.
Доказательство. Так как 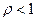 , то можно взять
, то можно взять 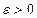 настолько малым, чтобы выполнялось неравенство
настолько малым, чтобы выполнялось неравенство 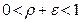 . Из условий
. Из условий 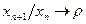 ,
, 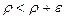 и следствия к теореме 2.5 вытекает, что при всех
и следствия к теореме 2.5 вытекает, что при всех 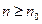 имеем верные неравенства
имеем верные неравенства 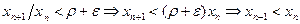 . Следовательно, последовательность
. Следовательно, последовательность 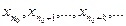 является убывающей, а также она ограничена снизу числом нуль. Поэтому эта последовательность имеет предел. Из 1-го утверждения в §5 вытекает, что последовательность
является убывающей, а также она ограничена снизу числом нуль. Поэтому эта последовательность имеет предел. Из 1-го утверждения в §5 вытекает, что последовательность 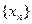 тоже имеет предел.
тоже имеет предел.
Докажем, что 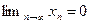 . Если предположить, что
. Если предположить, что 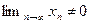 , то
, то
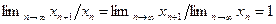 , (9.1)
, (9.1)
так как предел подпоследовательности 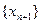 равен пределу последовательности
равен пределу последовательности 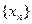 (2-е утверждение в § 2.5). По условию
(2-е утверждение в § 2.5). По условию 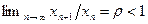 , чтопротиворечит равенству (9.1). Следовательно,
, чтопротиворечит равенству (9.1). Следовательно, 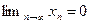 . ■
. ■
Примеры
9.2. Найти предел последовательности 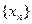 :
:
a) 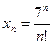 , б)
, б) 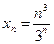
Решение
а) Найдем предел последовательности 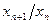 . Так как
. Так как 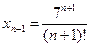 , то
, то
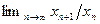 =
= 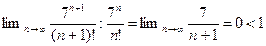 .
.
Из теоремы 2.13 следует, что 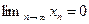 .
.
б) Найдем предел последовательности 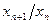 . Так как
. Так как 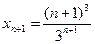 , то
, то
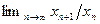 =
= 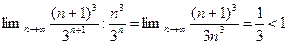 .
.
Из теоремы 2.13 следует, что 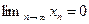 . ●
. ●
Задачи
9.1.Найти предел последовательности 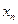 :
:
а) 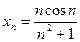 ; б)
; б) 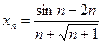 ; в)
; в) 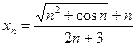 ; г)
; г) 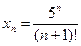 ;
;
д) 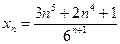 ; е)
; е) 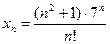 .
.
Бесконечно большие последовательности
Среди неограниченных последовательностей выделяют бесконечно большие последовательности. Именно, последовательность 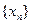 называется бесконечно большой, если для любого
называется бесконечно большой, если для любого 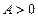 неравенство
неравенство 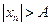 справедливо при всех
справедливо при всех 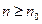 . В этом случае пишут
. В этом случае пишут 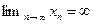 . Если ее члены положительны (отрицательны), то пишут
. Если ее члены положительны (отрицательны), то пишут 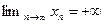
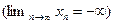 .
.
Замечание. Равносильны следующие утверждения:
1. 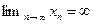
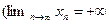 или
или 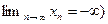 .+
.+
2. Для каждого числа 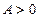 окрестность
окрестность 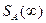
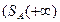 или
или 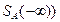 бесконечно удаленной точки содержит члены последовательности
бесконечно удаленной точки содержит члены последовательности 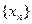 при всех
при всех 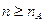 , где
, где 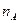 некоторое натуральное число.
некоторое натуральное число.
Доказательство следует из цепочки равносильных утверждений:
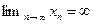
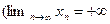 или
или 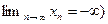
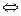
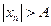
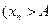 или
или 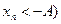 при всех
при всех 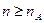
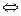
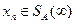
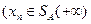 или
или 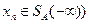 при всех
при всех 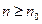 .▲
.▲
Последовательности 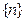 ,
, 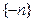 ,
, 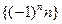 — примеры бесконечно больших последовательностей, причем
— примеры бесконечно больших последовательностей, причем 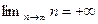 ,
, 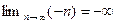 ,
, 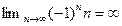 .
.
Бесконечно большая последовательность является неограниченной, но существуют неограниченные последовательности, которые не являются бесконечно большими. Например, последовательность 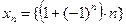 является неограниченной, так как содержит подпоследовательность
является неограниченной, так как содержит подпоследовательность 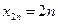 , но неравенство
, но неравенство 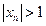 не выполняется для всех элементов с нечетными номерами.
не выполняется для всех элементов с нечетными номерами.
Теорема 2.14.Последовательность 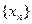 , члены которой не равны нулю, является бесконечно большой тогда и только тогда, когда последовательность
, члены которой не равны нулю, является бесконечно большой тогда и только тогда, когда последовательность 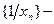 бесконечно малая.
бесконечно малая.
Доказательство. Возьмем любое 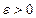 . Тогда число
. Тогда число 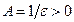 также произвольное число. Доказательство теоремы следует из следующей цепочки равносильных утверждений: последовательность
также произвольное число. Доказательство теоремы следует из следующей цепочки равносильных утверждений: последовательность 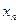 бесконечно большая
бесконечно большая 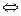
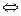
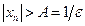 справедливо при всех
справедливо при всех 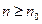
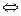
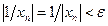 справедливо при всех
справедливо при всех 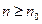
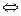 число
число 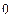 — предел последовательности
— предел последовательности 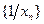
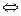 последовательность
последовательность 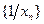 бесконечно малая. ■
бесконечно малая. ■
Следствия.
1.Если 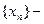 бесконечно большая последовательность,
бесконечно большая последовательность, 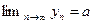 и число
и число 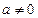 , то последовательность
, то последовательность 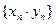 является бесконечно большой.
является бесконечно большой.
2.Если 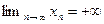 , то
, то 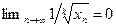 ;
;
Доказательство
1.Так как последовательность 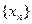 является бесконечно большой, то из теоремы 2.14 следует, что последовательность
является бесконечно большой, то из теоремы 2.14 следует, что последовательность 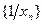 бесконечно малая. Для доказательства следствия достаточно установить, что последовательность
бесконечно малая. Для доказательства следствия достаточно установить, что последовательность 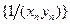 бесконечно малая. Применяя теоремы 2.7 и 2.8, имеем:
бесконечно малая. Применяя теоремы 2.7 и 2.8, имеем:
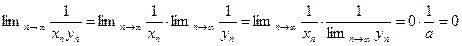 .
.
2.Из теоремы 2.14 следует, что последовательность 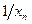 является бесконечно малой. Применяя теорему 2.12, имеем:
является бесконечно малой. Применяя теорему 2.12, имеем:
а) 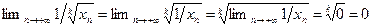 . ■
. ■
Примеры
9.3. Доказать, что последовательность 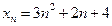 является бесконечно большой.
является бесконечно большой.
Решение. Так как последовательность 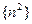 является бесконечно большой, а предел по
является бесконечно большой, а предел по
Дата добавления: 2016-06-05; просмотров: 3549;











