Рассмотрим элементарную ступень осевого компрессора.

Усилия на лопатках и работа вращения колесо ступени

Поворот потока воздуха в рабочем колесе сопровождается воз­никновением на каждой лопатке аэродинамической силы 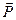, нап­равленной от вогнутой к выпуклой поверхности профиля.

Примем обозначения:

Р_u- окружная составляющая аэродинамической силы направленная параллельно вектору окружной скорости,

Р_а- осевая составляющая аэродинамической силы направленная вдоль оси двигателя.

Осевая составляющая Р_а передается на упорный подшипник вала компрессора. Окружная составляющая Р_u направлена против дви­жения лопаток колеса и стремятся замедлить их вращение. Поэто­му для поддержания постоянной частоты вращения ротора к валу компрессора должен быть приложен соответствующий крутящий момент.

Рассмотрим элементарную ступень осевого компрессора.

Определение: элемент ступени ОК, заключенный между двумя цилиндрическими поверхностями тока, расположенными на малом расстоянии друг от друга, называется элементарной ступенью ОК.

Работа, затрачиваемая на вращение РК такой ступени называется элементарной работой вращения:

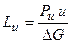, [Дж/кг] (3.1)

где 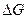- расход воздуха через элементарную ступень.

Для определения силы Р_u используем теорему Эйлера о количестве движения.

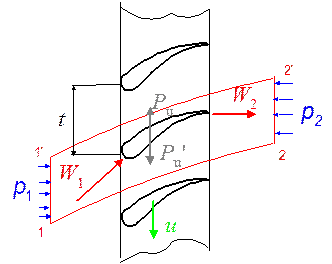Рассмотрим решетку профилей, представляющую собой развертку сечения лопаток РК в элементарной ступени на плоскость.

Определения: 1) расстояние между одина­ковыми точками соседних профилей называют шагом решетки t,

2) линию соединяющую передние кромки всех про­филей, называют фронтом решетки.

Выделим в потоке, обтекающем любой из профилей решетки, объем, ограниченный контрольной поверхностью, которая состоит из:

- двух поверхностей тока 1-2 и 1'-2', отстоящих друг от друга точно на величину шага t,

- двух плоскостей 1-1' и 2-2', парал­лельных фронту решетки и расположенных на таком расстоянии от нее, чтобы можно было пренебречь неравномерностью потока,

- двух плоскостей, параллельных плоскости рисунка, расположенных друг то друга на небольшом расстоянии Δr.

Обозначим:

Р- аэродинамическая сила действующая на одну лопатку PK со стороны потока ,

Р'- сила с которой лопатка воздействует на поток возду­ха,

Р = - Р'

Согласно теореме Эйлера, сумма всех сил, действующих на вы­деленный объем воздуха, должна быть равна разности коли­честв движения (импульсов) потоков, вытекающих и втекающих в этот объем в единицу времени. При этом силы, действующие на поверхностях 1-2 и 1'-2', вследствие периодичности потока в точности компен­сируют друг друга, а расход воздуха через эти поверхности равен нулю. Таким образом, кроме силы Р' будут подлежать учету толь­ко количества движения и силы давления воздуха в сечениях 1-1' и 2-2'.

Тогда, для окружной и осевой составляющих силы Р можно записать:

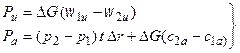. (3.2)

где 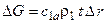- расход воздуха через контроль­ную поверхность.

С учетом (3.1) можно записать:

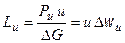, (3.3)

где .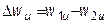

Таким образом, работа вращения колеса элементарной ступени осе­вого компрессора при цилиндрической поверхности тока равна произведению окружной скорости u и закрутки воздуха в колесе .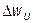

Если поверхности тока в данной элементарной ступени заметно отличаются от цилиндрических, то, применяя теорему Эйлера о моменте количества движения, можно получить:

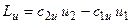. (3.4)

Формулы (3.3) и (3.4) определяют элементарную работу вращения L_u в одном сечении ступени ОК.

Работа вращения колеса ступени в целом может быть найдена путем интегрирования её значений для каждой элементарной ступени (с учетом расхода воздуха через неё) с последующим отношением результата интегрирования ко всему массовому расходу воздуха через ступень G_в :

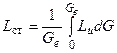. (3.5)

3.4. Изображение процесса сжатия воздуха в ступени в p, v- и T, s- координатах

Процесс сжатия (повышения давления) воздуха в ступени компрессора является, вообще говоря, неравновесным. Но степень этой неравновесности невелика, и поэтому его обычно условно изображают в различных термодинамических координатах. Рассмотрим процесс повышения давления воздуха в ступени компрессора в р, v- и T, s- координатах.

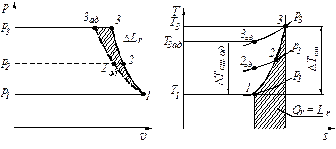
Изобары р = р₁ и р = р₃ соответствуют давлению воздуха перед и за ступенью. Точка 1 изображает состояние воздуха на входе в ступень. Линии 1-2 и 2-3 соответствуют процессам повышения давления в РК и НА.

В авиационных компрессо­рах теплообмен между потоком в компрессоре и окружающей средой на установив­шихся режимах пренебрежимо мал. Если бы, кроме то­го, воздух в компрессоре был бы лишен вязкости, то процесс повышения давления в ступени протекал бы при постоянной энтропии, т. е. по адиабате, изображенной линиями 1-3_ад.

В действительности выделение теплоты, связанной с трением в процессе сжатия при практическом отсутствии теплообмена с окружающей средой, приведет к некоторому увеличению температуры за ступенью по сравнению с температурой, достигаемой в адиабатном процессе. В результате реальный процесс сжатия изобразится линиями 1-3, расположенными правее адиабаты. а температура Т₃ за ступенью окажется выше Т_3ад .

Если принять, что увеличение энтропии в результате выделения теплоты трения опреде­ляется равенством 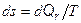, то суммарная теплота трения 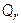будет связана с изменени­ем энтропии в реальном процессе 1-3 условием

,

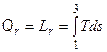откуда следует, что величина L_r может быть выражена в T, s- диаграмме площадью, лежащей между линией 1-3 и осью абсцисс.

Согласно уравнению Бернулли работа вращения колеса ступени, равна

,

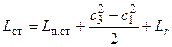где 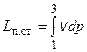- политропная работа сжатия (повышения давления) в ступени. Из рис. видно, что эта работа превышает работу повышения давления в адиабатном процессе 1-3_ад, равную 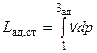, на величину, эквивалентную площади заштрихованного на рис. 3.5 криволинейного треугольника, обозначенной симво­лом ΔL_r . Поскольку это увеличение L_п.ст по сравнению с L_ад.ст явля­ется следствием выделения теплоты трения, в теории компрессоров его принято называть тепловым сопротивлением.

С учетом сказанного уравнение (2.1) может быть записано в виде

,

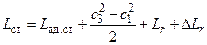откуда следует, что вредная роль гидравлических потерь проявляется в компрессорах двояко: как непосредственно в виде затраты работы L_r на преодоление гидравлических сопротивлений, так и дополнительно в виде теплового сопротивления ΔL_r .