Сила давления жидкости на плоские стенки
Сначала рассмотрим силы давления жидкости на горизонтальные стенки.
Сила давления жидкости на горизонтальное дно сосуда определяется по формуле (рис. 1.9):
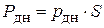 , (1.19)
, (1.19)
а давление на дно, согласно основному уравнению гидростатики, как:
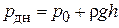 . (1.20)
. (1.20)
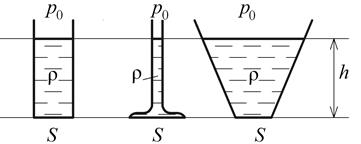
Рис. 1.9. Сила давления жидкости на горизонтальные стенки
ВЫВОДСледовательно, сила давления жидкости на горизонтальное дно зависит от давления на свободной поверхности 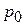 , плотности жидкости r, глубины погружения поверхности h, но не зависит от формы сосуда (гидростатический парадокс).
, плотности жидкости r, глубины погружения поверхности h, но не зависит от формы сосуда (гидростатический парадокс).
ОБЩИЙ СЛУЧАЙ
Рассмотрим более общий случай. Пусть площадь 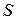 расположена под углом
расположена под углом 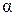 к горизонту и перпендикулярна к плоскости рисунка (рис. 1.10).
к горизонту и перпендикулярна к плоскости рисунка (рис. 1.10).
Через проекцию контура площади S (линия АВ) проведем ось оу
и спроектируем эту площадь на плоскость хоу.
Определим силу давления жидкости на элементарную площадку 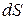 предполагая, что в пределах
предполагая, что в пределах 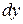 давление не меняется:
давление не меняется:
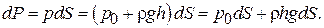
Здесь 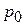 – давление на свободной поверхности, h – глубина погружения площадки dS. Заметим, что
– давление на свободной поверхности, h – глубина погружения площадки dS. Заметим, что 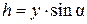 . Для определения полной силы
. Для определения полной силы 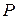 проинтегрируем полученное выражение по всей
проинтегрируем полученное выражение по всей
площади S.
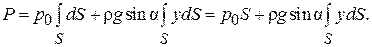
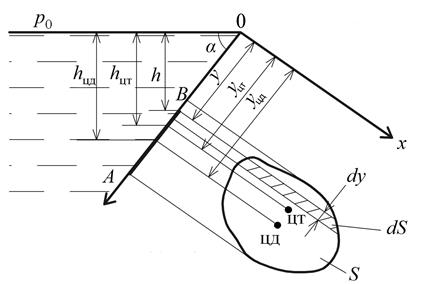
Рис. 1.10. Схема для определения силы давления жидкости
на плоскую стенку
Последний интеграл в правой части уравнения представляет собой статический момент площади 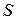 относительно оси ох и равен:
относительно оси ох и равен:
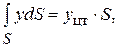
где 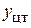 – координата центра тяжести площади
– координата центра тяжести площади 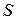 . Заменяя
. Заменяя 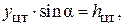 получим:
получим:
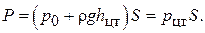 (1.21)
(1.21)
Здесь 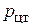 – давление в центре тяжести площади S. Полная сила давления на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.
– давление в центре тяжести площади S. Полная сила давления на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.
Формулу (1.21) представим в другом виде:
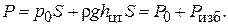 (1.22)
(1.22)
Здесь 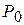 – внешняя сила,
– внешняя сила, 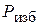 – избыточная сила, вызванная весом жидкости.
– избыточная сила, вызванная весом жидкости.
Внешнее давление 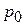 передается всем точкам площади S одинаково, поэтому внешняя сила
передается всем точкам площади S одинаково, поэтому внешняя сила 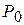 будет приложена в центре тяжести площади S. Сила избыточного давления
будет приложена в центре тяжести площади S. Сила избыточного давления 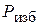 из-за неравномерности распределения избыточного давления по глубине приложена ниже в центре давления
из-за неравномерности распределения избыточного давления по глубине приложена ниже в центре давления 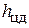 .
.
Координата центра гидростатического давления определяется по формуле:
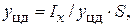 (1.23)
(1.23)
где 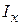 – момент инерции фигуры
– момент инерции фигуры 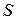 относительно оси ох.
относительно оси ох.
Зависимость (1.23) может быть представлена в виде:
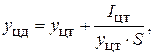 (1.24)
(1.24)
где 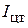 – момент инерции фигуры S относительно оси, проходящей через её центр тяжести.Величина
– момент инерции фигуры S относительно оси, проходящей через её центр тяжести.Величина 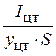 представляет собой эксцентриситет.
представляет собой эксцентриситет.
Зная величины 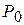 и
и 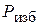 и точки их приложения, можно найти величину и точку приложения общей силы P.
и точки их приложения, можно найти величину и точку приложения общей силы P.
Дата добавления: 2018-05-10; просмотров: 815;










