Частные производные и полный дифференциал функций нескольких переменных
Содержание лекции: Частные производные функции нескольких переменных. Дифференцируемость и дифференциал функции.
Линеаризация функции. Касательная плоскость и нормаль к поверхности.
Производные и дифференциалы высших порядков.
1. Частные производные ФНП *)
Рассмотрим функцию и = f(P), РÎDÌRn или, что то же самое,
и = f( х1, х2, ..., хп).
Зафиксируем значения переменных х2, ..., хп, а переменной х1 дадим приращение Dх1. Тогда функция и получит приращение 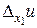 , определяемое равенством
, определяемое равенством
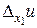 = f (х1+Dх1, х2, ..., хп) – f( х1, х2, ..., хп).
= f (х1+Dх1, х2, ..., хп) – f( х1, х2, ..., хп).
Это приращение называют частным приращением функции и по переменной х1.
Определение 7.1. Частной производной функции и = f( х1, х2, ..., хп) по переменной х1 называется предел отношения частного приращения 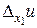 функции к приращению аргумента Dх1 при Dх1® 0 (если этот предел существует).
функции к приращению аргумента Dх1 при Dх1® 0 (если этот предел существует).
Обозначается частная производная по х1 символами
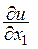 ,
, 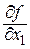 ,
, 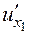 ,
, 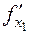 ,
, 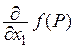 .
.
Таким образом, по определению
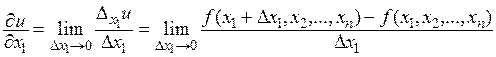
Аналогично определяются частные производные по остальным переменным х2, ..., хп. Из определения видно, что частная производная функции по переменной хi – это обычная производная функции одной переменной хi, когда остальные переменные считаются константами. Поэтому все ранее изученные правила и формулы дифференцирования могут быть использованы для отыскания производной функции нескольких переменных.
Например, для функции u = x3 + 3xy – z2 имеем
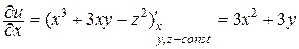
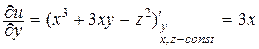
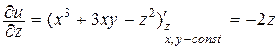
Таким образом, если функция нескольких переменных задана явно, то вопросы существования и отыскания ее частных производных сводятся к соответствующим вопросам относительно функции одной переменной – той, по которой необходимо определить производную.
Рассмотрим неявно заданную функцию. Пусть уравнение F(x, y) = 0 определяет неявную функцию одной переменной х. Справедлива
Теорема 7.1.
Пусть F(x0, y0) = 0 и функции F(x, y), F¢х(x, y), F¢у(x, y) непрерывны в некоторой окрестности точки (х0 , у0), причем F¢у(x0, y0) ¹ 0. Тогда функция у, заданная неявно уравнением F(x, y) = 0, имеет в точке (x0, y0) производную, которая равна
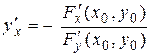 .
.
Если условия теоремы выполняются в любой точке области DÌ R2, то в каждой точке этой области 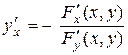 .
.
Например, для функции х3 –2у4 + ух + 1 = 0 находим
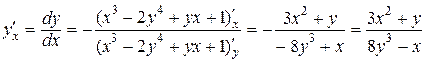 .
.
Пусть теперь уравнение F(x, y, z) = 0 определяет неявную функцию двух переменных. Найдем 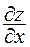 и
и 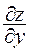 . Так как вычисление производной по х производится при фиксированном (постоянном) у, то в этих условиях равенство F(x, y=const, z) = 0 определяет z как функцию одной переменной х и согласно теореме 7.1 получим
. Так как вычисление производной по х производится при фиксированном (постоянном) у, то в этих условиях равенство F(x, y=const, z) = 0 определяет z как функцию одной переменной х и согласно теореме 7.1 получим
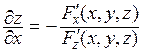 .
.
Аналогично 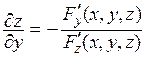 .
.
Таким образом, для функции двух переменных, заданной неявно уравнением 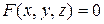 , частные производные находят по формулам:
, частные производные находят по формулам: 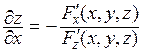 ,
, 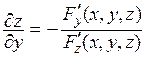
Рассмотрим функцию z = f(x, y). Пусть существуют производные 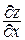 = fх¢(x, y) и
= fх¢(x, y) и 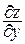 = fу¢(x, y). Так как эти производные сами являются функциями двух переменных, то можно поставить вопрос об их частных производных. Если такие производные существуют, то их называют частными производными второго порядка от функции z = f(x, y) и обозначают
= fу¢(x, y). Так как эти производные сами являются функциями двух переменных, то можно поставить вопрос об их частных производных. Если такие производные существуют, то их называют частными производными второго порядка от функции z = f(x, y) и обозначают
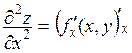 ,
, 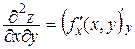 ,
, 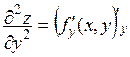 ,
, 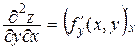 .
.
Производные 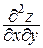 и
и 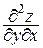 называются смешанными производными второго порядка. Наряду с приведенными обозначениями используются также обозначения
называются смешанными производными второго порядка. Наряду с приведенными обозначениями используются также обозначения
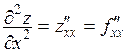 ,
, 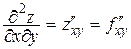 ,
, 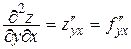 ,
, 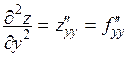 .
.
Дата добавления: 2017-11-21; просмотров: 2882;










