Система базисных функций
Сущность задач анализа реальных сигналов состоит в том, чтобы эти сигналы представить в виде совокупности простых элементарных сигналов, удобных для анализа. Реальный сигнал может быть представлен в виде суммы ортогональных составляющих (элементарных сигналов) [10]
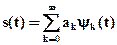 (1.1)
(1.1)
приt принадлежащемотрезку ортогональности [t1,t2]. Формула (1.1) называется разложением сигнала по системе базисных функций yk(t). Коэффициенты ak называются спектром разложения сигнала в ряд базисных функций.
К системе базисных функций предъявляются следующие требования:
- для любого сигнала ряд (1.1) должен сходиться;
- yk(t) должно иметь простую аналитическую форму;
- ak должны вычисляться аналитически просто.
Условие ортогональности базисных функций имеет вид
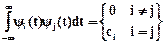 , (1.2)
, (1.2)
где число ci называют нормой базисной функции yi(t). Каждую базисную функцию можно нормировать по ее норме, причем нормированная функция имеет вид
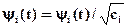 .
.
Система (1.2.) примет вид
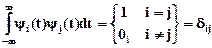 (1.3.)
(1.3.)
где dij - символ Кронекера.
Для определения ak умножим правую и левую части уравнения (1.1) на yk(t) и проинтегрируем обе части на отрезке ортогональности:
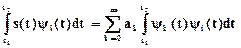 .
.
Приk=iправый интеграл равен единице, тогда
 . (1.4)
. (1.4)
Ортогональное разложение (1.1) называется обобщенным рядом Фурье, а коэффициенты ak - обобщенными коэффициентами Фурье. Набор чисел {ak} называется спектрами сигнала. Пример ортонормированных базисных функций – базис тригонометрического ряда Фурье на отрезке [-p,p]
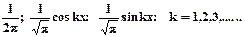 .
.
Аппроксимируем произвольную функцию x(t) линейной комбинацией n ортогональных функций
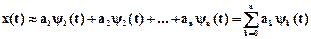 .
.
Определим постоянные ai, при которых среднеквадратическая величина s функции xl(t)®min, где
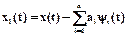 или
или 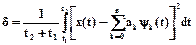 . (1.5)
. (1.5)
Из (1.5) следует, что s есть функция от ai и для ее минимизации необходимо принять 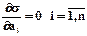 . Так как t2-t1ºconst, из (1.5) получим
. Так как t2-t1ºconst, из (1.5) получим
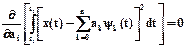 (1.6)
(1.6)
Если возвести в квадрат выражение в квадратных скобках под знаком интеграла, то в силу ортогональности все слагаемые вида

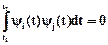 ,
,
т.е. производная всех слагаемых, не содержащих ai, равна нулю, и тогда
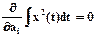 ,
, 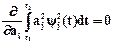 ,
, 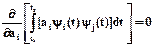 .
.
В формуле (1.6) останется два слагаемых
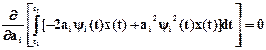 .
.
Изменив порядок интегрирования и дифференцирования, получим
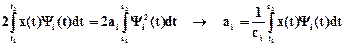 . (1.7)
. (1.7)
Если ai выбирать по формуле (1.7), то
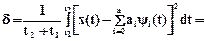
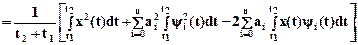 ,
,
Из формулы (1.7) следует, что 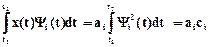 , тогда определим s
, тогда определим s
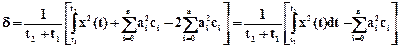 .
.
Дата добавления: 2022-05-27; просмотров: 179;










