Метод конечных элементов

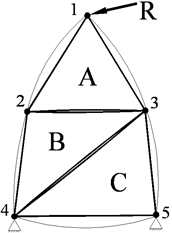
Рассмотрим использование метода конечных элементов на примере прочностного расчета пластины (рисунок 1, а). Пластина (показана тонкими линиями) нагружена силой R и жестко закреплена за основание. Аппроксимируем пластину тремя треугольными конечными элементами (КЭ) – A, B, C. Каждый КЭ соединяется с соседним только в своих вершинах – узлах. Для того чтобы это подчеркнуть, на рисунке *1 стороны некоторых треугольников искусственно отнесены друг от друга. Некоторые узлы принадлежат только одному КЭ (узлы 1 и 5), некоторые – сразу нескольким КЭ. Например, узел 2 принадлежит сразу и элементу А и элементу В; узел 3 принадлежит всем трем элементам, узел 4 – элементам В и С.

а)	б)

Рисунок 1 – Пример разбиения пластины на конечные элементы

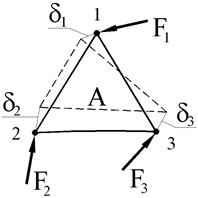
Предварительно рассмотрим какой-нибудь отдельный конечный элемент, например, А (рисунок 1, б). Со стороны остальных элементов и, в общем случае, со стороны внешней среды, на него действуют силы F₁, F₂, F₃. Под действием этих сил треугольник деформируется (показано штриховыми линиями). В результате деформации вершины треугольника переместятся на малые величины, соответственно, d₁, d₂, d₃.

Очевидно, существует связь между величинами сил и соответствующих им перемещений вершин элемента. Традиционно эта связь записывается в матричном виде:

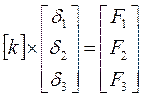
(1)

где k – т.н. матрица жесткости конечного элемента. Порядок ее получения для упругой треугольной пластины подробно рассматривается ниже. Пока же отметим, что компоненты матрицы жесткости зависят от координат вершин треугольника, толщины пластины и механических свойств материала (модуля упругости E и коэффициента Пуассона m).

Далее уравнения вида (1) для всех конечных элементов объединяют в общие матрицы – отдельно матрицу сил и отдельно в глобальную матрицу жесткости. Для этого достаточно сложить все элементы матриц конечных элементов, относящихся к одному узлу. Такой процесс называется ассемблированием.

При составлении матрицы сил силы, приложенные в одном и том же узле, но действующие от разных элементов, обозначим по имени элемента с индексом узла. Например, сила, с которой элемент В действует на 2-ой узел, равна В₂, а сила, с которой элемент А действует на тот же узел, равна А₂ и т.д. Заметим, что силы, с которыми элементы действуют друг на друга, по третьему закону Ньютона равны по величине, но противоположны по направлению. Например, можно записать: A₂ + B₂ = 0, A₃+B₃+C₃=0, B₄+C₄=0. Поэтому при формировании глобальной матрицы сил существует следующее правило: если узлы (в примере 2 и 3) свободны от воздействия внешних сил и закреплений, то соответствующие этим узлам элементы глобальной матрицы сил равны нулю.

В итоге система уравнений (в матричном виде), описывающая равновесие тела под действием заданных сил и закреплений, имеет вид:

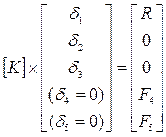
(3)

где К – глобальная матрица жесткости, полученная объединением локальных матриц жесткости каждого отдельного конечного элемента; R – внешняя сила, действующая на тело; F₄, F₅ – силы, действующие в закреплениях.

Запрет на перемещения в узлах 4 и 5 формально можно записать, как d₄=0 и d₅=0. Таким образом, в итоговой системе пяти уравнений (3) остается пять неизвестных, что позволяет найти ее решение – значения перемещений d_i в каждом узле. Зная перемещения вершин (узлов), по формуле (1) рассчитываются силы, действующие на каждый элемент. По значениям действующих сил нетрудно рассчитать вызванные ими напряжения в каждом элементе.