Нормальные формы формул логики высказываний
Высказывания и операции над ними, формулы
Сводка теории
Имена предметов называются индивидными (предметными) константами. В «грамматике» формального языка индивидные константы играют роль существительных.
Выражения, содержащие знаки «переменных» и превращающиеся в имена предметов, если вместо переменных подставить некоторые имена предметов, называются именными формами. Именные формы мы будем называть индивидными (предметными) переменными. Областью изменения индивидных переменных являются не только числа, но и совокупность любых индивидов (в частности, для нематематического языка – любые предметы или даже любые утверждения). В «грамматике» формального языка индивидные переменные играют роль местоимений.
Соединяя два имени чисел знаками равенства или неравенства, получаем записи некоторых утверждений – это высказывания, называемые еще пропозициональными переменными, если они содержат индивидные переменные.
Общее логико-философское определение этого понятия можно сформулировать так: высказывание – это мысленное отражение объективной связи между предметами. Оно истинно, если адекватно отражает эту связь, в противном случае – ложно. В естественном языке высказывание существует в виде повествовательного предложения. Если это предложение простое, т.е. описывает отдельный факт и не может быть разделено на более мелкие осмысленные предложения, то соответствующее высказывание называется простым.
В формальном языке высказывание представляется выражением, содержащим индивидные константы и некоторые специальные символы, обозначающие связь между ними. В математической логике высказывания рассматриваются лишь с позиции их свойства быть истинными или быть ложными, конкретное содержание высказываний игнорируется.
Роль союзов, с помощью которых в естественном языке из простых предложений формируются сложные, в формальном языке играют логические (или пропозициональные) связки, называемые также логическими операциями.
Будем интерпретировать логические связки как функции, определенные на так называемом булевом (по имени английского математика Дж. Буля) множестве В ={И, Л}, {«истина», «ложь»} или {1, 0}, со значениями в этом же множестве следующим образом:
| отрицание | 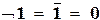 , , 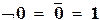 ; ;
|
| конъюнкция | 1&1 = 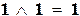 , , 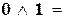 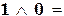 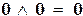 ; ;
|
| дизъюнкция | 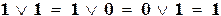 , , 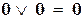 ; ;
|
| импликация | 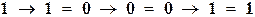 , ,  ; ;
|
| эквивалентность |  . .
|
Действие этих операций (связок) можно представить в виде символических таблиц, которые будем называть таблицами истинности данных логических операций. Например, для операции отрицания таблица истинности выглядит так:
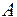
| 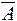
|
Именно эту таблицу (ее надо читать по строкам: «если 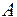 =1, то
=1, то 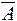 = = 0», т.е. одновременно
= = 0», т.е. одновременно 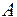 истинно и
истинно и 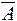 ложно) мы фактически и приняли в качестве определения операции отрицания.
ложно) мы фактически и приняли в качестве определения операции отрицания.
В технических приложениях операцию отрицания называют инверсией. Эту операцию можно условно проиллюстрировать работой следующей электрической цепи (рис. 1.1).
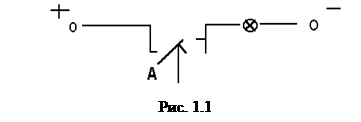
Действие в цепи: если 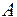 = 1, то кнопка нажата, цепь разомкнута и лампочка не горит, т.е.
= 1, то кнопка нажата, цепь разомкнута и лампочка не горит, т.е. 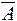 = 0; если
= 0; если 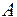 = 0, то цепь замкнута и лампочка горит, т.е.
= 0, то цепь замкнута и лампочка горит, т.е. 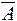 = 1.
= 1.
Таблица истинности для операции конъюнкции, соответствующей союзу «и» естественного языка, выглядит следующим образом:
| A | В | A^B |

В этой таблице каждая строка показывает, истинна или ложна конъюнкция при данном наборе истинных или ложных конъюнктивных членов. В технических приложениях операция конъюнкции называется логическим умножением. Эту операцию можно проиллюстрировать работой следующей электрической цепи (рис. 1.2).
Таблица истинности для операции дизъюнкции (аналог в естественном языке – союз «или») выглядит следующим образом:
| А | В | AÚB |
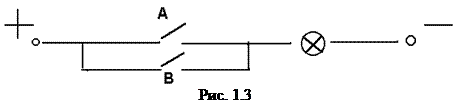
В технических приложениях операцию дизъюнкции называют логическим сложением. Простейшая электрическая цепь, иллюстрирующая эту операцию, имеет вид ( рис. 1.3).
В отдельных технических дисциплинах (а иногда и в математических теориях) используют и исключающее «или», приводящее к операции «альтернативная дизъюнкция», которую обозначают «+2» (а также « 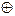 », «
», « 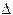 »). Примером такой операции в математике является сложение по модулю 2. Результаты операций A Ú B и A
»). Примером такой операции в математике является сложение по модулю 2. Результаты операций A Ú B и A 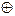 B отличны лишь в одной ситуации: когда A = 1 и B = 1 одновременно.
B отличны лишь в одной ситуации: когда A = 1 и B = 1 одновременно.
Таблица истинности для операции альтернативной дизъюнкции выглядит следующим образом:
| А | В | A 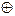 B B
|
Эту операцию можно проиллюстрировать работой следующей электрической цепи (рис.1.4).
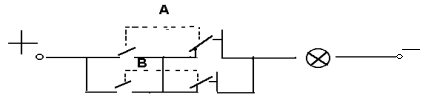
Таблица истинности для операции импликации (ближайший аналог в естественном языке – оборот «если..., то...») такова:
| A | В | A  B B
|
Соответствующая электрическая цепь имеет вид (рис. 1.5).

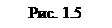
Приведем таблицу истинности для эквивалентности (соответствует оборотам естественного языка типа «тогда и только тогда, когда...», «для того, чтобы..., необходимо и достаточно...» и др.):
| A | В | A 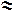 B B
|
Электрическая цепь, реализующая операцию эквивалентности, имеет вид (рис. 1.6)

Понятие формулы алгебры логики (высказываний) определим следующим образом:
1) пропозициональная переменная есть формула;
2) если А и В – формулы, то
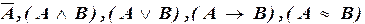 – формулы;
– формулы;
3) других формул, кроме построенных по пп. 1, 2, нет.
Подформулой формулы А называется любая ее часть, которая сама является формулой.
Каждая формула может интерпретироваться как функция, определенная на множестве В,со значениями в этом же множестве, полученная из  по правилам построения данной формулы. Значением формулы А при данных значениях переменных во множестве Вназывается значение функции, соответствующей формуле А, при этих значениях переменных.
по правилам построения данной формулы. Значением формулы А при данных значениях переменных во множестве Вназывается значение функции, соответствующей формуле А, при этих значениях переменных.
Формула называется выполнимой (опровержимой), если существует такой набор значений переменных, при которых эта формула принимает значение 1 (0).
Формула называется тождественно-истинной, или тавтологией (тождественно-ложной, или противоречием), если эта формула принимает значение 1 (0) при всех наборах значений переменных.
Примеры
Пример 1.1
Пусть X – высказывание «В огороде бузина», Y – высказывание «В Киеве дядька».
а) Записать с помощью формул логики высказываний следующие высказывания:
i) «В огороде бузина, а в Киеве дядька»;
ii) «Если неверно, что в огороде бузина, то, или в Киеве дядька, или в огороде бузина»;
iii) «Неверно, что если в Киеве нет дядьки и в огороде нет бузины, то, или в огороде бузина, или неверно, что в Киеве нет дядьки».
б) Записать на естественном языке высказывания, представленные следующими формулами:
i) 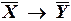 ;
;
ii) 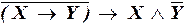 .
.
Решение
аi)  ;
;
аii)  ;
;
aiii) 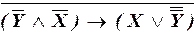 ;
;
бi) Если в огороде нет бузины, то в Киеве нет дядьки;
бii) Если неверно, что если в огороде бузина, то в Киеве дядька, то в огороде бузина, и в Киеве нет дядьки.
Пример 1.2
Разбить высказывание на элементарные и записать в виде формул логики высказываний:
а) «Функция непрерывна и дифференцируема»;
б) «Если функция не является непрерывной, то она недифференцируема»;
в) «Утверждение либо верно, либо неверно»;
г) «Теорема неверна или в доказательстве допущена ошибка»;
д) «Необходимое и достаточное условие счастья для шейха состоит в том, чтобы иметь вино, женщин и услаждать свой слух музыкой».
Решение
а)  , где X – «функция непрерывна», Y – «функция дифференцируема»;
, где X – «функция непрерывна», Y – «функция дифференцируема»;
б) 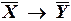 , где X – «функция непрерывна», Y – «функция дифференцируема»;
, где X – «функция непрерывна», Y – «функция дифференцируема»;
в)  , где А – «утверждение верно»;
, где А – «утверждение верно»;
г) 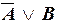 , где А – «теорема верна», В – «в доказательстве допущена ошибка»;
, где А – «теорема верна», В – «в доказательстве допущена ошибка»;
д) 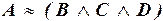 , где А – «шейх счастлив», В – «шейх имеет вино»; С – «шейх имеет женщин»; D – «шейх услаждает свой слух музыкой».
, где А – «шейх счастлив», В – «шейх имеет вино»; С – «шейх имеет женщин»; D – «шейх услаждает свой слух музыкой».
Пример 1.3
Пусть A – высказывание «Завтра экзамен», B – высказывание «Студент пишет шпаргалки».
Сформулировать словесно:
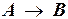 ;
; 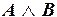 ;
; 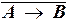 ;
;  ;
;  ;
; 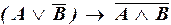 .
.
Решение
«Если завтра экзамен, то студент пишет шпаргалки»;
«Завтра экзамен и студент пишет шпаргалки»;
«Неверно, что если завтра экзамен, то студент пишет шпаргалки»;
«Если студент не пишет шпаргалки, то завтра нет экзамена»;
«Студент пишет шпаргалки в том и только том случае, когда завтра экзамен»;
«Если завтра экзамен или студент не пишет шпаргалки, то завтра нет экзамена, и студент не пишет шпаргалки».
Пример 1.4
Какой логической операции соответствует употребление «или» в высказываниях:
а) Родители разрешили завести или собаку, или кошку.
б) Кошелек или жизнь!
в) Либо студент сдает сессию, либо его отчисляют.
Решение
а) Альтернативная дизъюнкция, так как предполагается одно условие из двух, но не оба вместе.
б)Дизъюнкция (хотя, если говорящий «честен», то возможна альтернативная дизъюнкция).
в) Альтернативная дизъюнкция.
Пример 1.5
Тождественно ли истинны высказывания и формулы:
а) Если Земля столкнется с Солнцем, то пойдет дождь;
б)  ;
;
в) 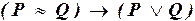 .
.
Решение
а) Тождественно-истинно, так как посылка – ложна, а из лжи следует все что угодно.
б) Импликация ложна в единственном случае, когда из истины следует ложь. Если 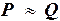 истинно, то P и Q принимают одинаковые истинностные значения. Значит, импликация
истинно, то P и Q принимают одинаковые истинностные значения. Значит, импликация 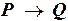 истинна и внешняя импликация – тоже. Если
истинна и внешняя импликация – тоже. Если 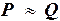 ложно, то внешняя импликация всегда истинна. Итак, вся формула – тождественно-истинна.
ложно, то внешняя импликация всегда истинна. Итак, вся формула – тождественно-истинна.
По-другому исследование можно провести, построив таблицу истинности для нашей формулы. Построим сокращенную таблицу истинности (т.е. для каждой переменной будем отводить только по одному столбцу, в месте ее первого вхождения в формулу; для каждой логической связки – тоже по одному столбцу, используя при этом запись самой формулы):
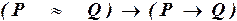
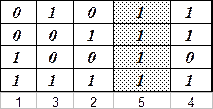
Здесь приведена сокращенная таблица истинности формулы: сначала заполняются столбцы возможных значений P и Q, таких наборов будет 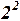 ; затем – столбцы для «внутренних» логических связок (эквивалентность и правая импликация) и, наконец, столбец для внешней (левой) импликации, который и дает истинностные значения всей формулы. Цифры под таблицей показывают порядок заполнения столбцов. Поскольку на любых наборах истинностных значений переменных формула принимает только значение 1, то она является тождественно-истинной.
; затем – столбцы для «внутренних» логических связок (эквивалентность и правая импликация) и, наконец, столбец для внешней (левой) импликации, который и дает истинностные значения всей формулы. Цифры под таблицей показывают порядок заполнения столбцов. Поскольку на любых наборах истинностных значений переменных формула принимает только значение 1, то она является тождественно-истинной.
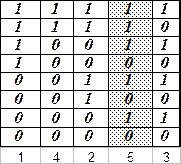
в) Рассмотрим сразу таблицу истинности:
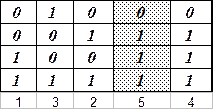
Поскольку формула может принимать оба истинностных значения (см. выделенный столбец), то она не является тождественно-истинной.
Пример 1.6
Составить таблицы истинности для формул:
а) 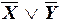 ;
;
б) 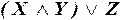 ;
;
в) 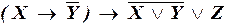 ;
;
г) 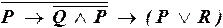 .
.
Решение
а) 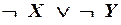

б) 
в) 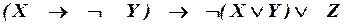
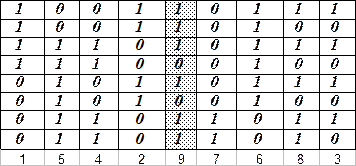
г) 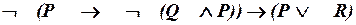

Задачи
1.1.Записать в виде формул логики высказываний, обозначив за переменные элементарные высказывания:
а) достаточные условия экстремума в точке для функции f(x);
б) необходимые условия экстремума в точке для функции f(x);
в) необходимые и достаточные условия экстремума в точке для функции f(x);
1.2.Определить, является ли данная последовательность формулой:
а) 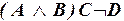 ;
;
б) 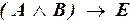 ;
;
в) 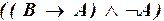 ;
;
г)  .
.
1.3.Сколькими способами можно расставить скобки в последовательности, чтобы получилась формула:
а) 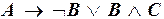 ;
;
б) 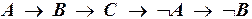 ?
?
1.4.Выписать все подформулы формулы:
а) 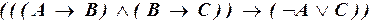 ;
;
б) 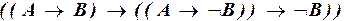 .
.
в) 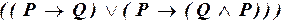 ;
;
г) 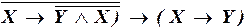 .
.
1.5.Составить таблицы истинности для формул;
а) 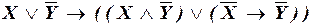 ;
;
б) 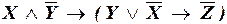 ;
;
в) 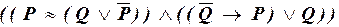 ;
;
г)  .
.
1.6.Доказать выполнимость формул:
а) 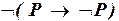 ;
;
б) 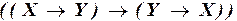 ;
;
в) 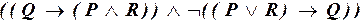 .
.
1.7. Доказать тождественную истинность формул:
а) 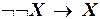 ;
;
б) 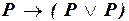 ;
;
в) 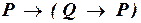 ;
;
г) 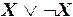 ;
;
д) 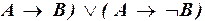 ;
;
е) 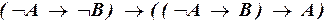 ;
;
ж) 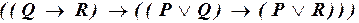 ;
;
з)  .
.
1.8.При каких значениях переменных X, Y, Z, U, V, W следующие формулы ложны:
а) 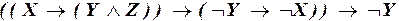 ;
;
б) 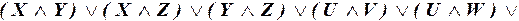
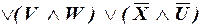 ;
;
в) 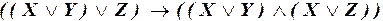 ;
;
г)  ;
;
д)  ?
?
1.2. Упрощение формул. Тождественные преобразования.
Доказательство равносильности, тождественной
истинности и тождественной ложности
формул и булевых функций
Сводка теории
При использовании формального определения формулы алгебры логики запись формул часто содержит «лишние» скобки, которыми можно пренебрегать без ущерба для смысла, если применять некоторые общепринятые правила.
Во-первых, в отдельно стоящих формулах (или если границы формулы ясны из контекста) можно опускать внешние скобки.
Во-вторых, как и арифметические операции, связки и кванторы можно упорядочить по их «силе», т.е. расположить в определенном порядке, считая, что те символы, которые в этом порядке находятся правее, «связывают сильнее», т.е. их следует выполнять в первую очередь:
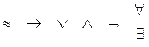
Таким образом, дизъюнкция и конъюнкция связывают сильнее, чем импликация, но слабее, чем отрицание. Конъюнкция связывает сильнее дизъюнкции. Слабее всего связывает эквивалентность. Равноправны в отношении связывания кванторы (об этом подробно в разделе 2), они связывают сильнее, чем любые логические связки.
По сравнению с общим определением формулы формального языка для формул логики высказываний (далее в этом разделе – просто формул) внесем следующие уточнения:
1) в качестве пропозициональных букв (индивидных переменных) будем рассматривать только простые высказывания x, y, z, ... 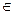 B, B={1,0};
B, B={1,0};
2) сложные формулы из простых будем строить только с помощью логических операций и скобок.
При таком подходе любая формула будет полностью определяться своей таблицей истинности.
Булевой функцией (или функцией алгебры логики,логической функцией) называется всякая функция n переменных (n= 1, 2, ...) с областью определения 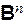 , множество значений которой содержится в B.
, множество значений которой содержится в B.
Любую булеву функцию можно, очевидно, задать таблицей истинности точно такого же вида, как те таблицы, которые сопоставляются формулам. Если таблица истинности, задающая булеву функцию f, совпадает с таблицей истинности некоторой формулы Ф, то говорят, что формула Ф представляет (или задает, или реализует ) функцию f.
Две формулы Ф и  называются равносильными(что обозначается Ф
называются равносильными(что обозначается Ф 
 ), если они представляют одну и ту же булеву функцию.
), если они представляют одну и ту же булеву функцию.
Для любых двух формул не представляет никаких трудностей проверить, равносильны ли они: достаточно сравнить их истинностные таблицы.
Булевы функции (от любого числа переменных), принимающие значение 1 независимо от значений аргументов, называются (как и реализующие их формулы) тавтологиями (или тождественно-истинными).
Булевы функции (и реализующие их формулы), всегда принимающие значение 0, называются противоречиями (или тождественно-ложными).
Убедиться в тождественной истинности или тождественной ложности конкретной формулы можно по той же таблице истинности (итоговый столбец таблицы будет содержать только соответствующую константу).
Другой способ доказательства равносильности формул или проверки их тождественной истинности или ложности состоит в использовании так называемых основных логических законов (основных равносильностей), обоснование которых можно провести путем построения соответствующих таблиц истинности. К основным логическим законам обычно относят следующие соотношения:
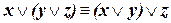
| (ассоциативность дизъюнкции) | (I.1) |
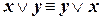
| (коммутативность дизъюнкции) | (I.2) |
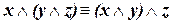
| (ассоциативность конъюнкции) | (I.3) |
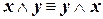
| (коммутативность конъюнкции) | (I.4) |
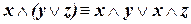
| (дистрибутивность конъюнкции по отношению к дизъюнкции) | (I.5) |

| (дистрибутивность дизъюнкции по отношению к конъюнкции) | (I.6) |

| (идемпотентность или «законы поглощения») | (I.7) (I.8) |
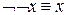
| («закон отрицания отрицания») | (II.1) |
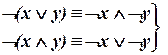
| («законы де Моргана») | (II.2) (II.3) |

| (III.1) | |
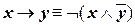
| (III.2) | |
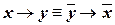
| («закон контрапозиции») | (III.3) |
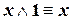
| (IV.1) | |
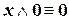
| (IV.2) | |

| (IV.3) | |

| (IV.4) | |
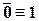
| (IV.5) | |
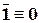
| (IV.6) | |
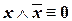
| («закон противоречия») | (IV.7) |
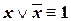
| («закон исключенного третьего») | (IV.8) |
Результаты вычислений таблиц истинности обеих частей равносильностей не зависят от того, как получены значения переменных, входящих в эти соотношения, т.е. от того, являются ли эти переменные независимыми или, в свою очередь, получены в результате каких-либо вычислений. Поэтому приведенные равносильности остаются справедливыми при подстановке вместо переменных любых логических функций и, следовательно, любых формул, представляющих эти функции. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной: при подстановке формулы Ф вместо переменной x все вхождения переменной x в исходное соотношение должны быть одновременно заменены формулой Ф.
Во всякой алгебре (в том числе и в булевой алгебре функций) соотношение
Ф 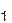
 Ф
Ф 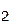 означает, что формулы Ф
означает, что формулы Ф 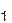 и Ф
и Ф 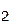 описывают одну и ту же булеву функцию f. Следовательно, если какая-либо формула Ф содержит Ф
описывают одну и ту же булеву функцию f. Следовательно, если какая-либо формула Ф содержит Ф 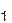 в качестве подформулы, то замена Ф
в качестве подформулы, то замена Ф 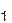 на Ф
на Ф 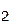 не изменяет элемента булевой алгебры f, над которым производятся операции в формуле Ф; поэтому Ф', полученная из Ф такой заменой, равносильна Ф. Это утверждение есть правило замены подформул, которое позволяет по имеющимся равносильностям получать формулы, равносильные данной.
не изменяет элемента булевой алгебры f, над которым производятся операции в формуле Ф; поэтому Ф', полученная из Ф такой заменой, равносильна Ф. Это утверждение есть правило замены подформул, которое позволяет по имеющимся равносильностям получать формулы, равносильные данной.
Отметим разницу между правилами подстановки и замены. При подстановке переменная заменяется на формулу; формула может быть любой, но требуется одновременная ее подстановка вместо всех вхождений переменной. При замене подформул заменяется любая подформула, однако не на любую другую, а только на равносильную ей. При этом замена всех вхождений исходной подформулы не обязательна.
Пусть имеется равносильность Ф 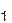
 Ф
Ф 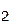 , где Ф
, где Ф 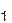 и Ф
и Ф 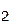 содержат переменную x. Если вместо всех вхождений x в Ф
содержат переменную x. Если вместо всех вхождений x в Ф 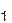 и Ф
и Ф 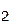 подставить произвольную формулу Ф, то получатся новые формулы Ф'
подставить произвольную формулу Ф, то получатся новые формулы Ф' 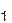 и Ф'
и Ф' 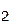 , причем не обязательно Ф
, причем не обязательно Ф 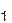
 Ф'
Ф' 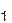 и Ф
и Ф 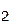
 Ф'
Ф' 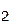 ; однако между собой новые формулы равносильны: Ф'
; однако между собой новые формулы равносильны: Ф' 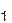
 Ф'
Ф' 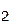 . Если же в Ф
. Если же в Ф 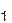 какую-либо подформулу заменить на равносильную ей, то получится новая формула Ф'
какую-либо подформулу заменить на равносильную ей, то получится новая формула Ф' 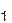 , равносильная Ф
, равносильная Ф 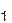 .
.
Такие преобразования, использующие равносильности формул (запас которых можно расширять с помощью правила подстановки) и правило замены, называются тождественными преобразованиями. Тождественные преобразования являются мощным средством доказательства равносильности формул и тождественной истинности или тождественной ложности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных (т.е. чем составление таблиц истинности).
Отметим, что «тактика» доказательства равносильности может быть разная: либо преобразуем одну из формул, приводя ее к виду другой, либо преобразуем обе формулы, приводя их к одной и той же формуле.
Примеры
Пример 1.7
Доказать равносильность формул, используя их таблицы истинности:
а) 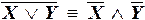 ;
;
б)  ;
;
в) 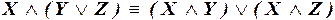 .
.
Решение
а) Сравним таблицы истинности для правой и левой частей:
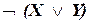
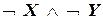

Итоговые столбцы таблиц истинности (выделены фоном) совпадают, значит, формулы равносильны.
б) 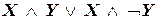
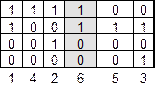
Итоговый столбец совпадает с первым столбцом, значит, эта формула равносильна Х.
в) 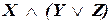
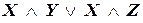

Пример 1.8
Исключить возможно большее число скобок:
а) 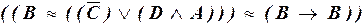 ;
;
б) 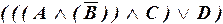 .
.
Ответы
а) 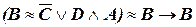 ;
;
б)  .
.
Пример 1.9
Восстановить максимальное число скобок, ориентируясь на формальное определение формулы:
а) 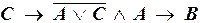 ;
;
б) 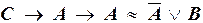 .
.
Ответы
а) 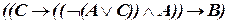 ;
;
б) 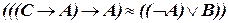 .
.
Пример 1.10
Оптимизировать формулы:
а)  ;
;
б)  .
.
Решение
а) Удаляя «лишние» скобки, получим:
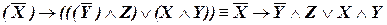 .
.
б) Применяя последовательно основные логические законы (III.2.), (II.1.), (I.5.), (IV.8.) и (IV.1.) и удаляя «по пути» скобки, получим:
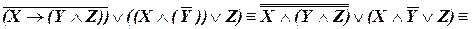

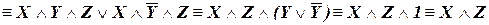 .
.
Пример 1.11
Доказать равносильность формул, используя логические законы:
а) 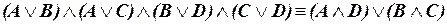 ;
;
б) 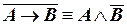 .
.
Решение
а) Преобразуем левую формулу к виду правой формулы, последовательно применив логические законы (I.6.), (I.6.) и (I.2.):
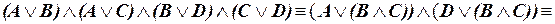
 .
.
б) Применим к левой формуле логические законы (III.1.), (II.2.) и (II.1.):
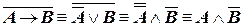 .
.
Пример 1.12
Определить, является ли формула тавтологией, противоречием или ни тем, ни другим:
а) 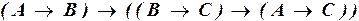 ;
;
б)  ;
;
в) 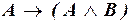 ;
;
г) 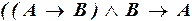 .
.
Решение
а) Приведем формулу к наиболее простому виду, последовательно исключая импликации по логическому закону (III.1.) и убирая двойные отрицания по закону (II.1.):
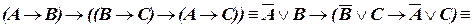
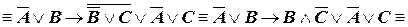
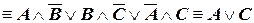 .
.
Полученная формула не является логической константой, следовательно, исходная формула не является ни тавтологией, ни противоречием.
б) Применим логические законы (II.2.), (IV.7.) и (IV.2.):
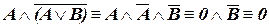 .
.
Исходная формула – противоречие.
в) Применим (III.1), (I.6), (IV.8) и (IV.1):
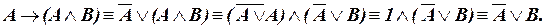
Исходная формула не является ни тавтологией, ни противоречием.
г) Применим (III.1), (II.3), (II.2), (II.1), (I.2), (IV.1), (I.5), (IV.3):
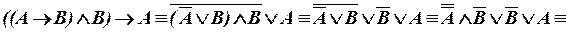
 Исходная формула не является ни тавтологией, ни противоречием.
Исходная формула не является ни тавтологией, ни противоречием.
Задачи
1.9.Доказать равносильность формул, используя таблицы истинности:
а)  ;
;
б) 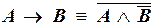 .
.
1.10.Доказать равносильность формул задачи 1.9, используя основные логические законы.
1.11.Доказать равносильность формул (некоторые из них часто тоже относят к основным логическим законам):
а) 
| (поглощение); |
б) 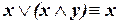
| (поглощение); |
в) 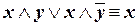
| (склеивание); |
г) 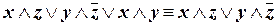
| (обобщенное склеивание); |
д) 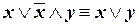
| |
е) 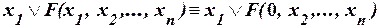 , ,
| где F – произвольная формула. |
1.12. Доказать, что:
а) 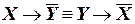 ;
;
б) 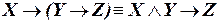 ;
;
в) 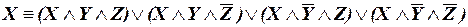 .
.
1.13.Построить формулу U такую, чтобы данная формула была тождественно истинной:
а)  ;
;
б)  .
.
1.14.Построить формулу от трех переменных, которая истинна в том и только в том случае, когда ровно две переменные ложны.
1.15.Построить формулу от трех переменных, которая принимает такое же значение, как и большинство (меньшинство) переменных.
Нормальные формы формул логики высказываний
Сводка теории
Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная или ее отрицание встречаются не более одного раза.
Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).
Следует отметить, что ДНФ функции (или формулы) может быть не единственной.
Алгоритм приведения к ДНФ может быть описан с привлечением приведенных ранее равносильностей или основных логических законов (см. разд. 1.2). Сначала с помощью закона (II.1) и законов де Моргана (II.2), (II.3) все отрицания «спускаются» до переменных. Затем раскрываются скобки, с помощью логических законов (I.7), (I.8), (IV.7) и (IV.8) удаляются лишние конъюнкции и повторения переменных в конъюнкциях, а с помощью логических законов (IV.1.) – (IV.6) удаляются константы.
Элементарная конъюнкция называется правильной, если в нее каждая переменная входит не более одного раза (включая ее вхождения под знаком отрицания).
Правильная элементарная конъюнкция называется полной относительно переменных 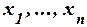 , если каждая из этих переменных входит в нее один и только один раз (может быть, под знаком отрицания).
, если каждая из этих переменных входит в нее один и только один раз (может быть, под знаком отрицания).
Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных 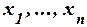 называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильны и полны относительно переменных
называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильны и полны относительно переменных 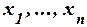 .
.
Поскольку из вида СДНФ бывают ясны ее переменные, будем говорить просто СДНФ, опуская слова: «относительно переменных 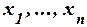 ».
».
Всякую ДНФ можно привести к СДНФ расщеплением конъюнкций, которые содержат не все переменные, например:
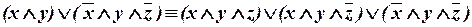 .
.
Если из формулы F с помощью некоторых равносильностей можно получить формулу Ф, то Дата добавления: 2022-05-27; просмотров: 136;
<== предыдущая лекция
|
следующая лекция ==>
Конструктивные особенности спортивной обуви | Общее представление об исчислении высказываний










