Общее представление об исчислении высказываний
Формулы логики предикатов и их преобразование
Сводка теории
Функция n переменных (n = 1,2,...) с непустой областью определения, множество значений которой содержится во множестве {1,0}, называется n-местным предикатом.
Если область определения n-местного предиката имеет вид 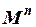 , т.е. все независимые переменные пробегают одно и то же множество, то говорят, что предикат определен на множестве М.
, т.е. все независимые переменные пробегают одно и то же множество, то говорят, что предикат определен на множестве М.
n-местный предикат может, в частности, принимать для всех наборов значений независимых переменных одно и то же значение, т.е. быть тождественно-истинным или тождественно-ложным.
Если в многоместном предикате фиксировать значения некоторых, но не всех независимых переменных, получается новый предикат с меньшим числом мест.
Если F – свойство элементов множества M и F(x) – соответствующий этому свойству предикат (определенный на M), то предложение: «все элементы множества M обладают свойством F» или «каждый (или любой, или всякий) элемент множества M обладает свойством F»- записывается в виде: 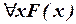 ; а предложение: «во множестве M существует (или есть, или имеется, или найдется) элемент, обладающий свойством F» – в виде
; а предложение: «во множестве M существует (или есть, или имеется, или найдется) элемент, обладающий свойством F» – в виде 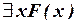 .
.
Читаются эти выражения так: «Для всякого (или для всех)  »; «Существует x такое, что F(x)».
»; «Существует x такое, что F(x)».
Выражения 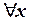 и
и  называются квантором общности (или всеобщности) и квантором существования соответственно. При этом обычно говорят: «квантор по переменной x».
называются квантором общности (или всеобщности) и квантором существования соответственно. При этом обычно говорят: «квантор по переменной x».
Можно рассматривать постановку квантора общности и квантора существования перед знаками предикатов («навешивание» кванторов или «квантификация») как особые операции.
Навешивание квантора общности есть операция, сопоставляющая одноместному предикату F(x) высказывание 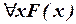 – истинное, если F(x)тождественно-истинен, и ложное в противном случае. Навешивание квантора существования есть операция, сопоставляющая одноместному предикату F(x) высказывание
– истинное, если F(x)тождественно-истинен, и ложное в противном случае. Навешивание квантора существования есть операция, сопоставляющая одноместному предикату F(x) высказывание 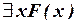 – ложное, если F(x) тождественно ложен, и истинное в противном случае.
– ложное, если F(x) тождественно ложен, и истинное в противном случае.
Операции навешивания кванторов общности и существования сопоставляют каждому n-местному предикату 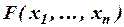 (n-1)-местные предикаты
(n-1)-местные предикаты  и
и  соответственно. В последних двух предикатах переменная
соответственно. В последних двух предикатах переменная  называется связанной, остальные переменные
называется связанной, остальные переменные  – свободными (или параметрами).
– свободными (или параметрами).
Логико-математический язык первого порядка (первой ступени) L задается набором из четырех множеств:
a) (индивидные) переменные x, y, z, ...;
b) n-местные (индивидные) функциональные символы F, G, H, ... для каждого n;
c) n-местные (индивидные) предикатные символы P, B, S, ... для каждого n;
d) логические связки и кванторы.
Любой 0-местный функциональный символ является (индивидной) константой, 0-местный предикатный символ – логической (пропозициональной) константой.
Если задан язык L, то можно определить некоторые правильно построенные тексты, составленные из символов L и вспомогательных символов – скобок и запятых. Эти тексты называются выражениями языка L и подразделяются на термы и формулы.
Определение
i) Переменная языка Lесть терм;
ii) если 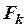 – k-местный функциональный символ языка L и
– k-местный функциональный символ языка L и  - термы, то выражение F(
- термы, то выражение F(  )есть терм языка L. Коротко это запишем в виде правила вывода:
)есть терм языка L. Коротко это запишем в виде правила вывода:
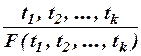 .
.
Это обобщенное индуктивное определение показывает, что каждый терм имеет один и только один вид из следующих двух: переменная или константа (из правила ii как 0-местная функция) языка L, либо функция от термов. Таким образом, термы – это те выражения языка, значениями которых являются индивиды. Роль термов состоит в том, чтобы описывать именные формы и имена индивидов.
Определение
Если P – k-местный предикатный символ языка L, а  суть термы, то выражение P(
суть термы, то выражение P(  ) называется атомарной (или элементарной) формулой.
) называется атомарной (или элементарной) формулой.
В частности, если P – пропозициональная буква (0-местный предикатный символ), то Pсама по себе является атомарной формулой.
Определение
i) Каждая атомарная формула есть формула;
ii) 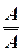 , т.е. если уже построена формула A, то разрешается построить новую формулу
, т.е. если уже построена формула A, то разрешается построить новую формулу  ; подобным образом следует трактовать и следующий пункт:
; подобным образом следует трактовать и следующий пункт:
iii)  , где
, где 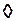 – любая логическая связка;
– любая логическая связка;
iv)  , т.е. если уже построена формула A, и x – произвольная переменная языка L, то разрешается построить новую формулу
, т.е. если уже построена формула A, и x – произвольная переменная языка L, то разрешается построить новую формулу 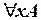 ; так же следует трактовать и следующий пункт:
; так же следует трактовать и следующий пункт:
v) 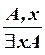 .
.
В формулах вида 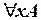 ,
, 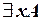 выражение
выражение 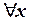 или
или  называют кванторной приставкой, x – переменной кванторной приставки, а формулу A – областью действия кванторной приставки.
называют кванторной приставкой, x – переменной кванторной приставки, а формулу A – областью действия кванторной приставки.
Как уже отмечалось, вхождение переменной x в формулу A может быть связанным (если оно попадает в область действия квантора по x или в саму кванторную приставку с переменной x) или свободным.
Заметим, что одна и та же переменная может иметь и свободные, и связанные вхождения в одну и ту же формулу. Переменная xназывается свободной переменной формулыA, или параметромA, если x входит (хотя бы один раз) свободно в A. Формула, не содержащая параметров, называется замкнутой (она является высказыванием).
Свободные и связанные переменные играют различные роли в формуле. Во-первых, вместо связанной переменной нельзя подставить конкретное значение – получится бессмысленное выражение. Во-вторых, связанная переменная не имеет самостоятельного значения, ее можно заменить на другую переменную, и смысл формулы от этого не изменится.
Все формулы: 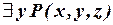 ,
, 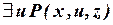 ,
, 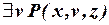 -выражают один и тот же предикат, одну и ту же функцию от x, z. Такая операция называется переименованием связанной переменной.
-выражают один и тот же предикат, одну и ту же функцию от x, z. Такая операция называется переименованием связанной переменной.
При переименовании связанной переменной смысл формулы не меняется, если при этом никакая свободная переменная в любой подформуле данной формулы не может после переименования оказаться связанной.
Например, если в формуле 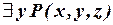 мы решим заменить переменную y на переменную x, то получится формула
мы решим заменить переменную y на переменную x, то получится формула 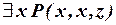 , которая имеет совершенно иной смысл, чем исходная формула. Формула
, которая имеет совершенно иной смысл, чем исходная формула. Формула 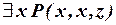 зависит уже лишь от одного параметра z, а не от двух. Причина состоит в том, что после неудачного переименования связанной переменной y первое вхождение переменной x, которое раньше было свободным, стало связанным. Это явление называют коллизией переменных при переименовании связанных переменных. Коллизия переменных недопустима.
зависит уже лишь от одного параметра z, а не от двух. Причина состоит в том, что после неудачного переименования связанной переменной y первое вхождение переменной x, которое раньше было свободным, стало связанным. Это явление называют коллизией переменных при переименовании связанных переменных. Коллизия переменных недопустима.
Главным рабочим инструментом в логике предикатов, как и в логике высказываний, служит понятие равносильности формул.
Определение
Формулы Ф и Yравносильны (Ф 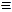 Y), если:
Y), если:
· множества их свободных переменных совпадают;
· при любом замещении входящих в формулы Ф и Y предикатных символов конкретными предикатами эти формулы переходят либо в один и тот же предикат, либо в высказывания, имеющие одно и то же истинностное значение (последнее – в случае, когда Ф и Y замкнуты, т.е. множества их свободных переменных пусты).
Разумеется, все вхождения одного и того же предикатного символа как в Ф, так и в Y должны замещаться одним и тем же предикатом.
Определение
Формула называется тождественно-истинной (тождественно-ложной), если при любом замещении входящих в нее предикатных символов конкретными предикатами она переходит в тождественно-истинный (тождественно-ложный) предикат (если она не замкнута) или в истинное (ложное) высказывание (если она замкнута).
Замечания
1) Тождественно-истинная формула и тождественно-истинный предикат – не одно и то же. Тождественная истинность конкретного предиката относится только к его области определения, в то время как тождественная истинность формулы – это «абсолютная истинность», истинность для любых предметных областей. Аналогично – для тождественной ложности.
2) Из определения непосредственно следует, что формула 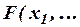
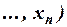 со свободными переменными
со свободными переменными 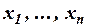 тождественно-истинна тогда и только тогда, когда тождественно-истинна формула
тождественно-истинна тогда и только тогда, когда тождественно-истинна формула 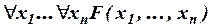 .
.
3) Отрицание тождественно-истинной формулы есть, очевидно, формула тождественно-ложная, а отрицание тождественно-ложной – тождественно-истинная.
Для расширения возможностей тождественных преобразований формул логики предикатов используются основные свойства кванторов.
I) Перестановка одноименных кванторов:
 ; (I.1)
; (I.1)
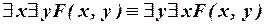 . (I.2)
. (I.2)
2) Связь между разноименными кванторами:
 ; (II.1)
; (II.1)
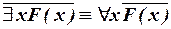 . (II.2)
. (II.2)
3) Вынесение кванторов за скобки:
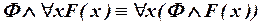 ; ;
| (где Ф не содержит свободной переменной x) | (III.1) |
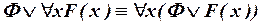 ; ;
| (III.2) | |
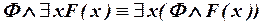 ; ;
| (III.3) | |
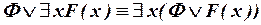 . .
| (III.4) |
Замечание
Условие, чтобы формула Ф не содержала свободной переменной x, в соотношениях (III.1 – III.4) является существенным: если оно не выполнено, то соотношения могут нарушаться (после вынесения квантора переменная x в формуле Ф из свободной может превратиться в связанную).
4) Переименование связанных переменных:
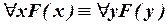 ; ;
| (вместо x и y можно брать любые другие переменные) | (IV.1) |
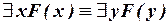 . .
| (IV.2) |
Замечание
Все введенные равносильности останутся справедливыми, если заменить в них F(x) (соответственно F(x, y)) любой формулой G, содержащей свободную переменную x (соответственно x и y) и, возможно, также и другие свободные переменные.
Отметим в общем виде самый простой из частных случаев, когда для доказательства равносильности формул логики предикатов удается воспользоваться средствами логики высказываний.
Утверждение 2.1
Если в равносильных формулах логики высказываний заменить элементарные высказывания произвольными предикатными символами так, чтобы одно и то же элементарное высказывание заменялось в обеих формулах одним и тем же символом, то возникающие при этом формулы логики предикатов будут также равносильны.
Утверждение 2.2
Если в тождественно-истинной формуле логики высказываний заменить элементарные высказывания произвольными предикатными символами, то возникающая при этом формула логики предикатов также тождественно-истинна (то же справедливо для тождественно-ложных формул).
С помощью свойств кванторов можно производить над формулами логики предикатов тождественные преобразования, причем ввиду утверждения 2.1 в этих преобразованиях можно использовать также любые равносильности логики высказываний. Производя тождественные преобразования в определенном порядке, можно для каждой формулы получить ей равносильную, имеющую особенно простое строение.
Примеры
Пример 2.1
Записать фразы в виде формул логики предикатов, указав области определения используемых предикатов:
а) если х делится на у и у делится на z, то х делится на z;
б) х – простое число.
Решение
а) Разбивая фразу на простые предложения, видим, что используется только одно свойство двух объектов, поэтому введем предикат 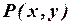 = «
= « 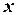 делится на
делится на 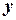 «. Речь идет, очевидно, о делимости нацело, поэтому областью определения предиката будет множество целых чисел:
«. Речь идет, очевидно, о делимости нацело, поэтому областью определения предиката будет множество целых чисел: 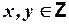 .
.
Структура всей фразы описывается конструкцией «если..., то...», значит, самой внешней (последней) связкой нашей формулы будет импликация. Посылка этой импликации описывается конъюнкцией простых предложений, поэтому итоговая формула имеет вид:
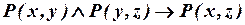 .
.
б) Самый простой подход: ввести предикат  = «
= « 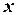 – простое число», который и описывает всю фразу.
– простое число», который и описывает всю фразу.
Но математические термины должны быть определены однозначно (что такое «простое» число, которое записывается одной цифрой? или которое записано с помощью повторения одной цифры? или которое можно легко запомнить или записать?), поэтому точный смысл этой фразы может быть воспроизведен с помощью строгого определения. То есть « 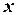 делится только на 1 и на себя» или, еще точнее, «либо
делится только на 1 и на себя» или, еще точнее, «либо 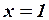 , либо
, либо 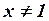 и если
и если 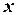 делится на любое
делится на любое 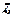 , то, или
, то, или 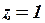 , или
, или 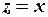 «.
«.
В последней фразе использован предикат делимости 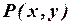 (см. пункт а), предикат равенства
(см. пункт а), предикат равенства 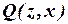 = «
= « 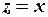 « и квантор всеобщности. Поскольку понятие простого числа обычно вводят только для натуральных чисел, то
« и квантор всеобщности. Поскольку понятие простого числа обычно вводят только для натуральных чисел, то 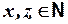 . Формула, описывающая последнюю фразу, имеет вид:
. Формула, описывающая последнюю фразу, имеет вид:
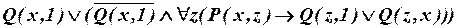 .
.
Пример 2.2
Указать свободные и связанные вхождения переменных в формулы:
а) 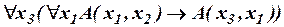 ;
;
б)  ;
;
в)  .
.
Решение
Проанализируем область действия каждого квантора, отмечая связанные вхождения общей прямой с засечками снизу, а свободные вхождения переменных стрелочкой сверху. Отметим, что в третьей формуле F и G – функциональные символы (в теориях первого порядка аргументом предиката не может выступать другой предикат).
¯ ¯




 а)
а) 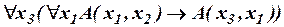 ;
;
¯ ¯ 



 б)
б)  ;
;
¯ 










 в)
в)  .
.
 |
Пример 2.3
Доказать тождественную истинность формул:
а)  ;
;
б) 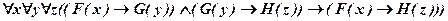 .
.
Решение
Будем преобразовывать бескванторную часть формул, используя основные логические законы.
а) 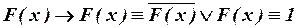 . Значит, исходная формула тождественно истинна.
. Значит, исходная формула тождественно истинна.
б) 

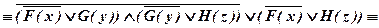
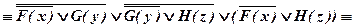
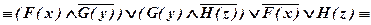
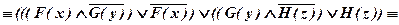
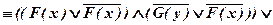
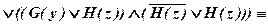
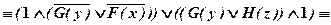
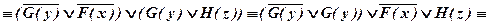
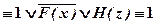 .
.
Значит, исходная формула тождественно истинна.
Пример 2.4
Доказать тождественную ложность формул:
а) 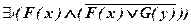 ;
;
б) 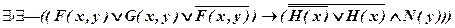 .
.
Решение
Будем преобразовывать бескванторную часть формул, используя основные логические законы.
а) 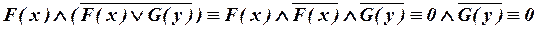 .
.
Значит, исходная формула тождественно ложна.
б) 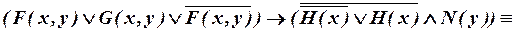
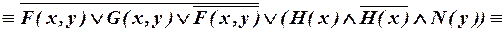

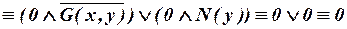 .
.
Значит, исходная формула тождественно ложна.
Задачи
2.1.Записать фразы в виде формул логики предикатов, указав области определения используемых предикатов:
а) «Если произведение двух чисел делится на простое число, то на него делится хотя бы один из сомножителей»;
б) «Через всякую точку, не лежащую на прямой, можно провести прямую, перпендикулярную данной»;
в) «Через каждые две точки можно провести прямую, причем, если эти точки различны, то такая прямая единственна»;
г) «Когда у некоего деятеля денег в избытке, он может воспевать что угодно, в том числе и отсутствие денег»;
д) «Всякий кулик свое болото хвалит, а чужое хает».
2.2.Пусть 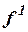 – одноместный,
– одноместный, 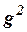 – двухместный,
– двухместный, 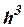 – трехместный функциональные символы. Являются ли термами следующие слова:
– трехместный функциональные символы. Являются ли термами следующие слова:
а)  ;
;
б) 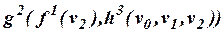 ;
;
в) 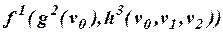 ?
?
2.3. Пусть 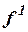 ,
, 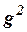 ,
, 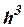 – те же, что и в задаче 2.2,
– те же, что и в задаче 2.2, 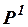 – одноместный,
– одноместный, 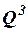 – трехместный предикатные символы. Являются ли формулами следующие слова:
– трехместный предикатные символы. Являются ли формулами следующие слова:
а) 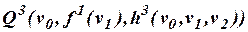 ;
;
б) 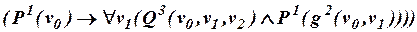 ;
;
в)  ;
;
г) 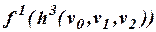 ?
?
2.4.Выписать все подформулы формулы:
а) 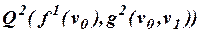 ;
;
б) 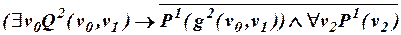 .
.
2.5.
а) Найти такие два замещения предикатного символа 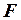 конкретным предикатом в формуле
конкретным предикатом в формуле 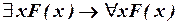 , чтобы при одном замещении получилось истинное предложение, при другом – ложное.
, чтобы при одном замещении получилось истинное предложение, при другом – ложное.
б) То же для формулы  .
.
в) То же для формулы  .
.
2.6.Доказать тождественную ложность формул:
а)  ;
;
б) 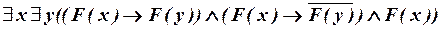 .
.
2.7.Доказать, что:
а) 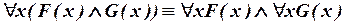 ;
;
б) 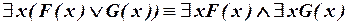 .
.
2.2. Приведение формул к предваренной
нормальной форме (ПНФ)
Сводка теории
Определение
Предваренной (или пренексной) формулой называется формула вида  , где Qiсуть кванторы, а формула A (называемая матрицей предваренной формулы) уже кванторов не содержит.
, где Qiсуть кванторы, а формула A (называемая матрицей предваренной формулы) уже кванторов не содержит.
Если  и B – предваренная формула, то B называют предваренной (нормальной) формой (ПНФ) формулы A.
и B – предваренная формула, то B называют предваренной (нормальной) формой (ПНФ) формулы A.
В частности, не исключается и случай n= 0, т.е. бескванторная формула также считается предваренной.
Теорема 2.1
Для всякой формулы существует ПНФ.
Доказательство. С помощью основных логических законов устраняем в формуле все знаки логических операций, кроме  (если таковые имеются).
(если таковые имеются).
К полученной формуле последовательно применяем в произвольном возможном порядке преобразования двух типов: А и В.
Преобразование типа А. Находим в формуле некоторую часть (подформулу) Ф, имеющую вид  , или
, или 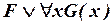 , или
, или 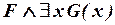 , или
, или  , где F, G(x) – какие-то формулы и G(x) содержит свободную переменную x. Пусть для определенности
, где F, G(x) – какие-то формулы и G(x) содержит свободную переменную x. Пусть для определенности 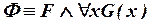 (в остальных случаях все делается точно так же).
(в остальных случаях все делается точно так же).
Преобразуем Ф следующим образом: проверяем, содержит ли F переменную x, и если нет, то замещаем Ф на 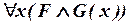 (соотношение (III.1)), если да, то заменяем все вхождения x в
(соотношение (III.1)), если да, то заменяем все вхождения x в 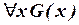 вхождениями какой-либо новой переменной, скажем, t, не встречающейся в нашей «боль-шой» формуле (соотношение (IV.1)), и затем заменяем
вхождениями какой-либо новой переменной, скажем, t, не встречающейся в нашей «боль-шой» формуле (соотношение (IV.1)), и затем заменяем 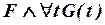 на
на 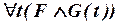 . Таким же образом поступаем с подформулами остальных трех видов (это возможно ввиду коммутативности конъюнкции и дизъюнкции).
. Таким же образом поступаем с подформулами остальных трех видов (это возможно ввиду коммутативности конъюнкции и дизъюнкции).
Преобразование типа В. Находим в формуле некоторую подформулу, имеющую вид 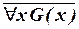 (или
(или 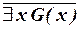 ), где G(x) – формула со свободной переменной x, и заменяем ее на
), где G(x) – формула со свободной переменной x, и заменяем ее на  (соответственно на
(соответственно на 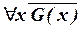 ) по соотношениям (II.1), (II.2).
) по соотношениям (II.1), (II.2).
Применяя преобразования типов А и В, мы шаг за шагом «вытаскиваем наружу» все кванторы и, в конце концов, приходим к формуле, в которой ни один квантор не стоит внутри конъюнкции или дизъюнкции, или вслед за отрицанием. Но в такой формуле квантор может стоять только либо вслед за другим квантором, либо в самом начале формулы, т.е. получена ПНФ для исходной формулы.
Замечания
1) В доказательстве указан практический способ приведения формул к ПНФ. При фактическом приведении удобно «по пути» устранять двойные отрицания всякий раз, когда они возникают (а также производить любые другие упрощения, если они возможны).
2) В силу соотношений II. 1 – II 2 отрицание формулы  равносильно формуле
равносильно формуле 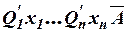 , где
, где  – квантор, «противоположный» Qi.
– квантор, «противоположный» Qi.
Помимо рассмотренных предваренных формул (и соответственно ПНФ), иногда вводят и более специальные виды нормальных форм, например, нормальную форму Сколема, которая имеет предваренный вид (т.е. все кванторы вынесены в начало формулы), не содержит функциональных символов и все ее кванторы всеобщности предшествуют кванторам существования либо, наоборот, все кванторы существования предшествуют кванторам всеобщности (понятно, что к такой форме легко перейти от ПНФ, используя свойства кванторов группы II).
Примеры
Пример 2.5
Привести формулы к ПНФ:
а)  ;
;
б) 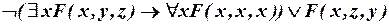 .
.
Решение
Преобразуем формулы, устраняя «лишние» логические связки и «опуская» отрицания на предикаты, а затем последовательно «вытаскива-ем» кванторы из-под логических связок с помощью преобразований типа А или типа В, при необходимости применяя переименование переменных.
а) 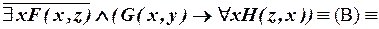
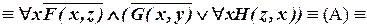
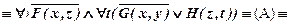
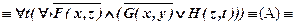
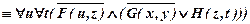 .
.
б) 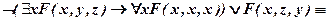
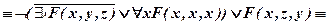
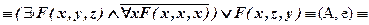

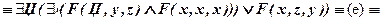
 .
.
Задачи
2.8.Привести к ПНФ:
а) 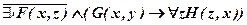 ;
;
б) 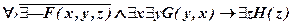 ;
;
в) 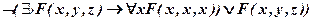 ;
;
г)  ;
;
д) 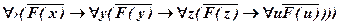 ;
;
е)  ;
;
ж) 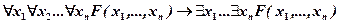 ;
;
з) 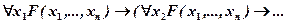
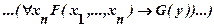 .
.
Контрольные вопросы
1. Дайте общее определение предиката. Что такое «местность» предиката? тождественно-истинный предикат? тождественно-ложный предикат?
2. Как определяются логические операции над предикатами?
3. Чем отличается формула логики высказываний от формулы логики предикатов?
4. Что такое интерпретация формулы логики предикатов? Параметр формулы? Замкнутая формула?
5. Что называют коллизией переменных?
6. Какие формулы логики предикатов называют равносильными? Конгруэнтными? Тождественно-истинными? Тождественно-ложными?
7. Дайте определение кванторов существования и всеобщности в случае одноместного и многоместного предиката.
8. Попробуйте доказать свойства кванторов.
9. Какие понятия формального языка выполняют роли, аналогичные тем, которые в естественном языке выполнятся: подлежащим? Сказуемым? Дополнениями? Местоимением? Союзами?
10. Что такое терм? Функциональная сложность терма?
11. Что такое формула? Логическая сложность формулы?
12. Что такое предваренная нормальная форма?
3. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ И ИСЧИСЛЕНИЕ
ПРЕДИКАТОВ
Общее представление об исчислении высказываний
Сводка теории
Таблицы истинности позволяют ответить на многие важные вопросы, касающиеся логических связок: является ли данная формула тавтологией, противоречием или ни тем и ни другим; влечет ли она логически другую данную формулу или являются ли две формулы логически равносильными.
Более сложные вопросы логики уже не могут быть решены с помощью истинностных таблиц или каких-либо других подобных эффективных процедур. Поэтому используется другой метод – аксиоматический.
При формализации математической теории полностью отвлекаются от ее содержания. Теоремы воспринимаются просто как формулы, которые могут быть выведены по определенным правилам. Поэтому формальные теории иначе называют исчислениями. О знаках и формулах исчисления приходится, однако, рассуждать содержательно: так, рядом с формальной теорией возникает «метатеория», которая тоже пользуется некоторыми обозначениями. Эти обозначения метатеории следует строго отличать от знаков и формул, относящихся к собственно формальной теории.
Существует много вариантов формализации логики высказываний. Опишем подробнее один из них; назовем его «теория L». Формальная (аксиоматическая) теория L считается определенной, если выполнены следующие условия:
1) Задано некоторое счетное множество символов теории L(языка теории). Основные символы теории Lсуть: пропозициональные буквы  , ...,
, ...,  , ... ; логические связки
, ... ; логические связки 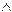 , Ú,
, Ú,  , Ø ; скобки (, ).
, Ø ; скобки (, ).
Конечные последовательности символов теории называются выражениями теории L.
2) Имеется подмножество выражений теории L, называемых формулами теории и определяемых индуктивно с помощью следующих двух пунктов:
i) пропозициональные буквы суть формулы L;
ii) если A и B – формулы, то формулами являются и следующие выражения: 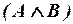 ,
, 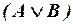 ,
, 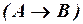 ,
,  .
.
3) Выделено некоторое множество формул, называемых аксиомами теории L, в рассматриваемом варианте теории их десять:
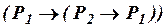 , (ив1)
, (ив1)
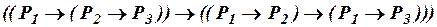 , (ив2)
, (ив2)
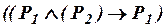 , (ив3)
, (ив3)
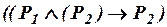 , (ив4)
, (ив4)
 , (ив5)
, (ив5)
 , (ив6)
, (ив6)
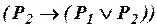 , (ив7)
, (ив7)
 , (ив8)
, (ив8)
 , (ив9)
, (ив9)
 (ив10)
(ив10)
Здесь 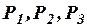 – конкретные пропозициональные переменные, так что (ив1) – (ив10) есть список из десяти конкретных формул языка L.
– конкретные пропозициональные переменные, так что (ив1) – (ив10) есть список из десяти конкретных формул языка L.
4) Принимаются правила вывода, по которым можно из уже установленных теорем получать новые. В теории L – два таких правила вывода.
Первое правило имеет вид (MP) 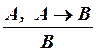 .
.
Это правило, называемое modus ponens (правило заключения), утверждает, что если формулы 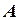 и
и 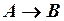 установлены как теоремы, то формула
установлены как теоремы, то формула 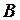 также является теоремой.
также является теоремой.
Второе правило имеет вид: (S)  .
.
Здесь 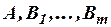 суть формулы,
суть формулы, 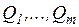 – попарно различные пропозициональные буквы. Через
– попарно различные пропозициональные буквы. Через 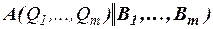 обозначен результат одновременного замещения всех вхождений букв
обозначен результат одновременного замещения всех вхождений букв 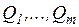 в
в 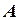 на формулы
на формулы 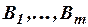 соответственно. Отметим, что это правило подстановки (S)можно применять и к пропозициональным буквам
соответственно. Отметим, что это правило подстановки (S)можно применять и к пропозициональным буквам 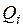 , которые вовсе не входят в
, которые вовсе не входят в 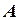 . В этом случае соответствующее
. В этом случае соответствующее 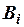 никуда не подставляется и просто не играет никакой роли.
никуда не подставляется и просто не играет никакой роли.
Выводом назовем любую конечную последовательность формул 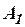 ,
, 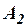 ,...,
,..., 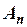 , такую, что каждая формула этой последовательности есть либо аксиома, либо совпадает с какой-либо предыдущей формулой этой последовательности, либо получается из каких-то предыдущих формул этой последовательности с помощью одного из правил вывода. Скажем, что вывод
, такую, что каждая формула этой последовательности есть либо аксиома, либо совпадает с какой-либо предыдущей формулой этой последовательности, либо получается из каких-то предыдущих формул этой последовательности с помощью одного из правил вывода. Скажем, что вывод 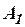 ,
, 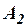 ,...,
,..., 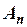 является выводом своей последней формулы
является выводом своей последней формулы 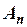 , и формулу
, и формулу 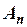 назовем выводимой, или, что то же самое, теоремой теории. Будем записывать это в виде: L
назовем выводимой, или, что то же самое, теоремой теории. Будем записывать это в виде: L 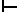 A или просто
A или просто 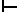 A.
A.
В дальнейшем будем употреблять сокращенный вывод, когда в качестве 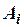 могут стоять теоремы теории L, полученные раньше, имея в виду, что мы всегда можем дополнить вывод, вставляя недостающие его отрезки.
могут стоять теоремы теории L, полученные раньше, имея в виду, что мы всегда можем дополнить вывод, вставляя недостающие его отрезки.
Примеры
Пример 3.1
Вывести в теории L теорему (A  A).
A).
Решение
Возьмем в качестве примера первой формулы вывода 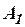 аксиому (ив2). Применим к ней правило подстановки в виде:
аксиому (ив2). Применим к ней правило подстановки в виде:
( 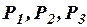
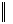 A, (A
A, (A  A), A).
A), A).
Получим
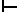 ((A
((A  ((A
((A  A)
A)  A))
A))  ((A
((A  (A
(A  A))
A))  (A
(A  A))). (а)
A))). (а)
Из аксиомы (ив1) подстановкой (