Оценка области параметрических ограничений, заданной в виде интервала изменения параметров
Рассмотрим подход к оценке области 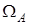 , заданной в виде
, заданной в виде
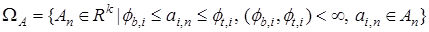 , (20)
, (20)
на основе анализа НИП и метода секущих для объекта
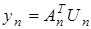 , (21)
, (21)
где 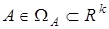 — вектор параметров, принадлежащий ограниченной области
— вектор параметров, принадлежащий ограниченной области 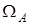 (20) с неизвестными параметрами
(20) с неизвестными параметрами 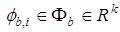 ,
, 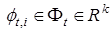 .
.
Для объекта (21) имеется информация 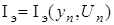 и получен наблюдаемый информационный портрет
и получен наблюдаемый информационный портрет 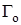 .
.
Введем вектор 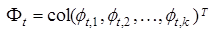 , который мажорирует вектор
, который мажорирует вектор 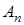 в (21). Рассмотрим частный случай области
в (21). Рассмотрим частный случай области 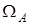 , соответствующей верхней границе области ограничений
, соответствующей верхней границе области ограничений
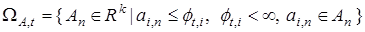 .
.
Для оценки вектор 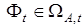 можно применить математическую модель
можно применить математическую модель
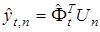 . (22)
. (22)
Ставится задача: для объекта (21) на основе анализа данных 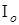 и отображения
и отображения 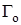 получить оценки вектора
получить оценки вектора 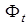 в (20) с помощью модели (22) таким образом, чтобы выполнялось условие доминирования
в (20) с помощью модели (22) таким образом, чтобы выполнялось условие доминирования
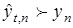 для почти
для почти 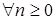 . (23)
. (23)
Под доминированием будем понимать выполнение неравенства 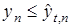 для почти
для почти 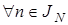 .
.
Для решения задачи может применяться несколько подходов. Изложим один из них, основанный на проверке условия доминирования, используя в качестве вторичного критерия математическое ожидание исследуемых переменных.
Рассмотрим проекции НИП 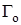 на плоскости
на плоскости 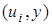 и построим секущие
и построим секущие 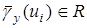
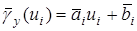 ,
, 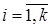 (24)
(24)
со следующими областями определения и значений:
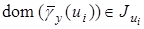 ,
, 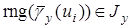 ,
,
где 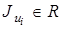 ,
, 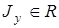 — интервалы изменения переменных
— интервалы изменения переменных 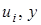 ;
; 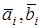 — некоторые числа.
— некоторые числа.
Полагаем 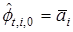 и получаем приближенную оценку области
и получаем приближенную оценку области 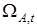
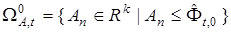 ,
,
где 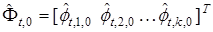 . Неравенство
. Неравенство 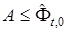 понимается как поэлементное.
понимается как поэлементное.
Индекс 0 обозначает уровень подстройки вектора 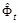 модели (22) и не совпадает с шагом изменения интервала
модели (22) и не совпадает с шагом изменения интервала 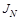 .
.
Далее по модели (22) с 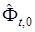 находим прогноз
находим прогноз 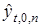 выхода объекта
выхода объекта 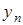 и величину коэффициента взаимной корреляции
и величину коэффициента взаимной корреляции 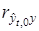 . Проверяем условие доминирования
. Проверяем условие доминирования
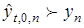 .
.
Если оно выполняется для почти всех 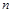 , то полагаем
, то полагаем 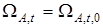 и процесс определения области параметрических ограничений на этом заканчиваем. В противном случае применяем алгоритм коррекции области
и процесс определения области параметрических ограничений на этом заканчиваем. В противном случае применяем алгоритм коррекции области 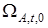 , который обеспечивает выполнение условия доминирования.
, который обеспечивает выполнение условия доминирования.
Алгоритм коррекции состоит в следующем. Вычисляем математические ожидания для 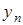 и
и 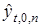
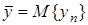 ,
, 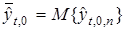
и определяем величину
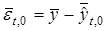
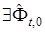 . (25)
. (25)
Лемма. 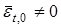 .
.
Величина 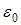 показывает насколько переменная
показывает насколько переменная 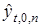 “недотягивает” до области доминирования над
“недотягивает” до области доминирования над 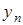 . Если
. Если 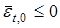 , то
, то 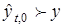 п. н.
п. н.
На основе 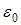 формируем множество поправок вектора
формируем множество поправок вектора 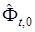 . Для этого находим величины
. Для этого находим величины
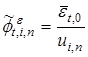
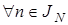 , (26)
, (26)
для которых определяем математические ожидания 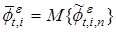 . Далее формируем вектор поправок
. Далее формируем вектор поправок
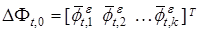 . (27)
. (27)
Так как необходимо обеспечить условие доминирования, то коррекцию вектора 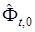 осуществляем по формуле
осуществляем по формуле
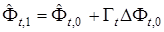 , (28)
, (28)
где 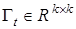 — диагональная матрица с
— диагональная матрица с 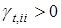 , и с помощью модели (22) определяем прогноз
, и с помощью модели (22) определяем прогноз 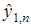 для
для 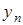
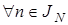 . Далее находим
. Далее находим 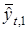 и
и 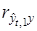 . Если окажется, что
. Если окажется, что 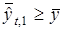 и
и
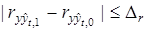 ,
, 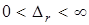 ,
,
то полагаем 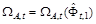 и на этом процесс построения области параметрических ограничений заканчивается. В противном случае адаптация вектора
и на этом процесс построения области параметрических ограничений заканчивается. В противном случае адаптация вектора 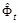 должна продолжаться.
должна продолжаться.
Утверждение 1. Если начальное значение вектора 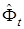 определяется на основе секущих (24), а его коррекция в уравнении (22) осуществляется согласно (27), (28), то оценка области параметрических ограничений
определяется на основе секущих (24), а его коррекция в уравнении (22) осуществляется согласно (27), (28), то оценка области параметрических ограничений
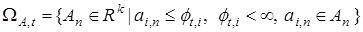 (29)
(29)
является допустимой, если выполняется условие доминирования 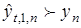 для почти
для почти 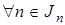 и
и
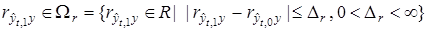 . (30)
. (30)
Условие (30) накладывает ограничение на класс допустимых моделей (22). За центр области 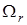 принимается значение
принимается значение 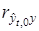 .
.
| Замечания | |
| @ | 1. В (26) вместо 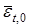 можно использовать текущее (по времени можно использовать текущее (по времени 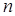 ) значение невязки ) значение невязки 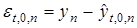 . 2. Если процессы в системе носят стохастический характер, то для принятия решения о доминировании следует установить допустимый уровень доминирования (см. ниже). . 2. Если процессы в системе носят стохастический характер, то для принятия решения о доминировании следует установить допустимый уровень доминирования (см. ниже).
|
Итак, в общем случае алгоритм адаптации вектора 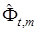 можно записать в виде
можно записать в виде
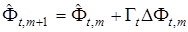 , (31)
, (31)
где 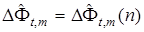 и формируется согласно изложенной выше процедуре.
и формируется согласно изложенной выше процедуре.
Для оценки качества работы системы идентификации параметров области 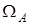 введем количественный критерий. Будем считать, что
введем количественный критерий. Будем считать, что 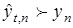 почти на всем интервале
почти на всем интервале 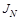 , если вероятность
, если вероятность
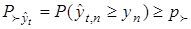
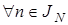 , (32)
, (32)
где 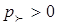 — заданная величина.
— заданная величина.
Определение. Вектор 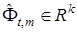 будем называть оптимальным, если он позволяет получить допустимую оценку области параметрического оценивания будем называть оптимальным, если он позволяет получить допустимую оценку области параметрического оценивания 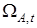 и обеспечивает при этом максимальное значение показателя и обеспечивает при этом максимальное значение показателя 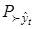 . .
|
Утверждение 2. Выход модели (22) с вектором 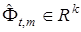 , соответствующим оптимальной мажоритарной оценке области
, соответствующим оптимальной мажоритарной оценке области 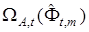 , имеет максимальную информационную мощность.
, имеет максимальную информационную мощность.
Алгоритм (31) относится к классу конечно-сходящихся. Его свойства следуют из следующей теоремы.
Теорема 1. Система идентификации (21), (22), (31) с допустимым вектором параметров 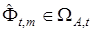 будет иметь ограниченные траектории, если матрица
будет иметь ограниченные траектории, если матрица 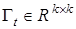 в алгоритме (22) удовлетворяет неравенству
в алгоритме (22) удовлетворяет неравенству
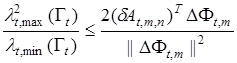 ,
,
где 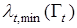 ,
, 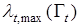 — минимальное и максимальное собственные числа матрицы
— минимальное и максимальное собственные числа матрицы 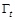 . Оптимальное значение матрицы
. Оптимальное значение матрицы 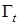 равно
равно
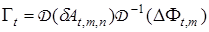 .
.
где 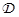 — оператор преобразования вектора
— оператор преобразования вектора 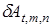 в диагональную матрицу.
в диагональную матрицу.
Аналогично ищется минорирующая оценка для области 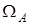 (21). В этом случае условие доминирования (23) записывается в виде
(21). В этом случае условие доминирования (23) записывается в виде
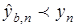 для почти
для почти 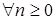 ,
,
где 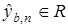 — выход модели
— выход модели
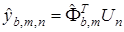 (33)
(33)
с вектором параметров 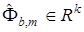 , настраиваемым с помощью алгоритма
, настраиваемым с помощью алгоритма
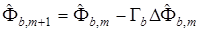 .
.
Невязка вектора 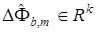 формируется согласно (26), (27) с учетом замечания. В (33)
формируется согласно (26), (27) с учетом замечания. В (33) 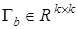 является диагональной матрицей с
является диагональной матрицей с 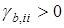 .
.
Пример. Рассмотрим объект (22) с вектором параметров
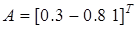
и действующим на выходе аддитивным ограниченным возмущением 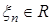 ,
, 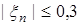 . Вектор
. Вектор 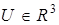 . Необходимо оценить область параметрических ограничений (28).
. Необходимо оценить область параметрических ограничений (28).
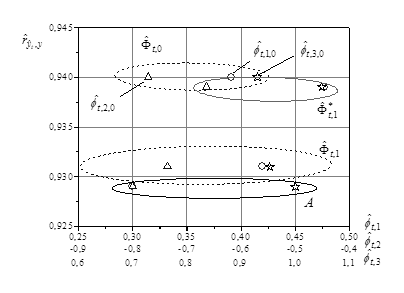
Рис. 7. Оценивание вектора F
На рис. 7 показаны результаты идентификации вектора 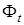 для области
для области 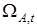 с помощью системы (22), (26), (31). Здесь приведен также вектор параметров
с помощью системы (22), (26), (31). Здесь приведен также вектор параметров 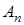 объекта (21). На основе метода наименьших квадратов получена следующая оценка вектора
объекта (21). На основе метода наименьших квадратов получена следующая оценка вектора 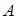 :
: 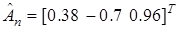 . Векторы
. Векторы 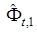 и
и 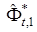 определялись с помощью алгоритма (31) с
определялись с помощью алгоритма (31) с 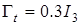 и
и 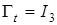 , где
, где 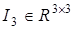 — единичная матрица. Соответствующие значения
— единичная матрица. Соответствующие значения 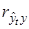 равны
равны 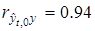 ,
, 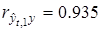 ,
, 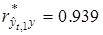 .
.
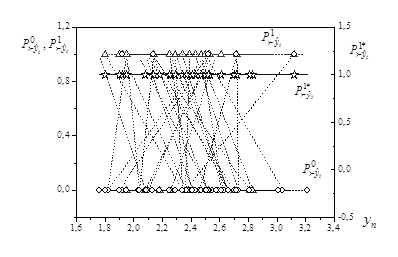
Рис. 8. Доминирование переменной 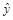 при различных значениях
при различных значениях
вектора 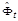
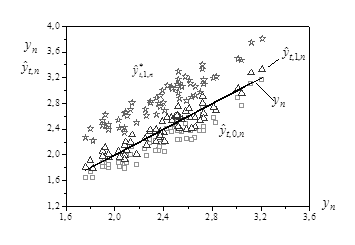
Рис. 9. Оценки выхода модели (22) в пространстве 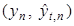
Согласно утверждению 1 полученные оценки являются допустимыми. Для принятия окончательного решения находим показатели доминирования с помощью (32). Для каждой из найденных оценок они равны (рис. 8)
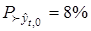 ,
, 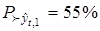 ,
, 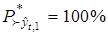 .
.
Эти же результаты подтверждает информационный портрет (рис. 9) в пространстве 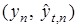 . Минорируюшая оценка для
. Минорируюшая оценка для 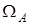 имеет вид:
имеет вид:
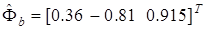 .
.
Дата добавления: 2017-02-13; просмотров: 728;










