ДЛЯ ОБЪЕКТОВ С САМОВЫРАВНИВАНИЕМ
Тип регулятора Оптимальный переходный процесс
____________________________________________________________________________
апериодический колебательный с 20 % - ным колебательный с мини-
перерегулированием мальной площадью
П K P = 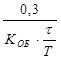 K P =
K P = 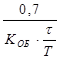 K P =
K P = 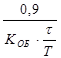
ПИ K P = 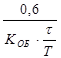 K P =
K P = 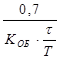 K P =
K P = 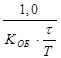
T И = 0,8 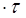
 0,5
0,5 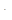 T T И =
T T И = 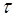
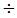 0,3
0,3 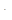 T T И =
T T И = 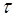
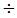 0,35
0,35  T
T
ПИД K Р = 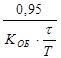 K P =
K P = 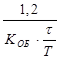 K P =
K P = 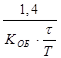
T И = 2,4 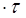 T И = 2,0
T И = 2,0 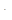
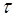 T И = 1,3
T И = 1,3 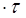
T ДИФ = 0,4 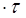 T ДИФ = 0,4
T ДИФ = 0,4 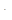
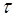 T ДИФ = 0,5
T ДИФ = 0,5 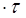
Построение переходных процессов.Построение переходных процессов в САУ,
вызванных основными для данной системы воздействиями, является завершающим этапом исследования системы. Существуют две группы методов построения пере-ходных процессов: аналитические и графические с использованием частотных характеристик.
Аналитические методы основаны на решении дифференциального уравнения системы. Общая методика решения дифференциальных уравнений приведена в раз-деле 2.2.5. В качестве конкретного примера рассмотрим построение переходного процесса по возмущающему воздействию при регулировании уровня ёмкости.
САУ описывается следующими уравениями:
Уравнение объекта –
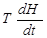 + H = K Y S Y + K B S B. (2.125)
+ H = K Y S Y + K B S B. (2.125)
Уравнение ПИ – регулятора –
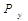 =
= 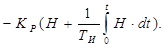 . (2.126)
. (2.126)
Уравнение исполнительного механизма –
S Y = P Y. (2.127)
Подставляя значение S y в уравнение (2.125), получим
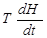 +
+ 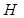 +
+ 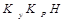 +
+ 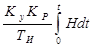 =
= 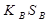 . (2.128)
. (2.128)
После дифференцирования имеем уравнение системы регулирования
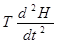 +
+ 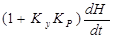 +
+ 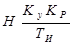 =
= 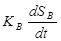 . (2.129)
. (2.129)
Допустим, что в некоторый момент t= 0 возникло ступенчатое возмущение
S B = 1.
Начальные условия:
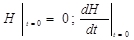 =
= 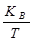 .(2.130)
.(2.130)
Последнее условие получено из уравнения (2.128) при t = 0 и S B = 1.
Характеристическое уравнение системы (2.129) имеет вид
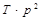 +
+ 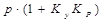 +
+ 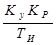 = 0 . (2.131)
= 0 . (2.131)
Корни уравнения (2.131) равны
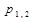 =
= 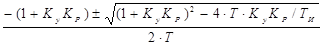 , (2.132)
, (2.132)
Если корни 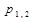 вещественные, то решение дифференциального уравнения имеет вид
вещественные, то решение дифференциального уравнения имеет вид
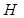 =
= 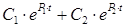 . (2.133)
. (2.133)
Постоянные интегрирования С 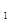 и С
и С 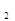 определим из начальных условий.
определим из начальных условий.
При t = 0 из уравнения (2.133) имеем
0 = С 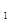 + С
+ С 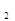 . (2.134)
. (2.134)
Дифференцируя уравнение (2.133) при t = 0 имеем
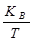 =
= 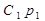 +
+ 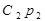 . (2.135)
. (2.135)
Из уравнений (2.134) и (2.135) определяем С 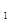 и С
и С 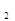
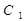 = -
= - 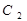 =
= 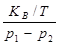 . (2.136)
. (2.136)
Подставляя значения С 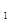 и С
и С 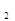 в уравнение (2.133) окончательно будем иметь решение в виде
в уравнение (2.133) окончательно будем иметь решение в виде
 =
= 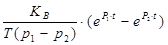 . (2.137)
. (2.137)
По уравнению (2.137) может быть построен график переходного процесса (рис. 30.)
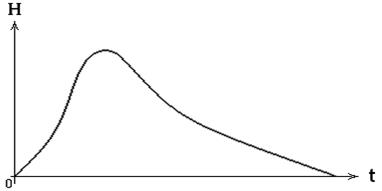
Рис. 30.
Графические методы построения переходных процессов основаны на примене-нии частотных характеристик.
Амплитудно-фазовую характеристику замкнутой САУ можно представить в виде
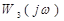 =
= 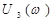 +
+ 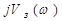 . (2.138)
. (2.138)
Переходная функция связана с действительной частотной характеристикой выра-жением
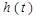 =
= 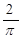
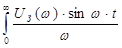
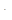
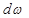 . (2.139)
. (2.139)
С помощью выражения (2.139) можно построить искомую переходную функцию h(t) путём графического нахождения входящих в неё интегралов по заданному гра-фику частотной характеристики U 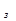 (
( 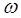 ). Методика такого построения, разработан-ная В.В. Солодовниковым, называется методом трапеции. Действительную харак-теристику U
). Методика такого построения, разработан-ная В.В. Солодовниковым, называется методом трапеции. Действительную харак-теристику U 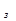 (
( 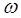 ) заменяем ломаной линией (рис.31,а). В результате U
) заменяем ломаной линией (рис.31,а). В результате U 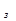 (
( 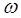 ) пред-ставляем алгебраической суммой нескольких трапеций U
) пред-ставляем алгебраической суммой нескольких трапеций U 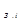 (
( 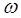 ) (трапеции 1 – 3 на рис.31,б). Соответственно искомую переходную характеристику h(t) можно запи-сать в виде алгебраической суммы нескольких составляющих, каждая из которых определяется одной из трапеций, т.е.
) (трапеции 1 – 3 на рис.31,б). Соответственно искомую переходную характеристику h(t) можно запи-сать в виде алгебраической суммы нескольких составляющих, каждая из которых определяется одной из трапеций, т.е.
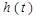 =
= 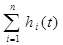 , (2.140)
, (2.140)
где
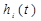 =
= 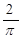
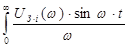
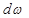 .
.
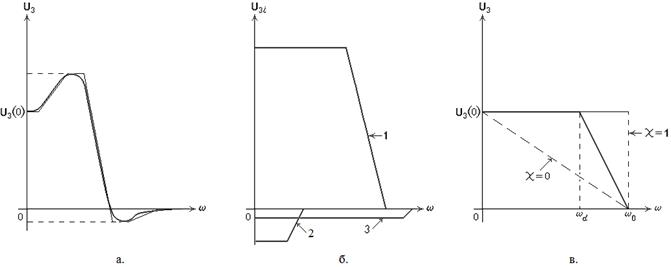
Рис. 31. Построение переходной характеристики.
Для характеристики, изображённой на рис.31.а, получаются три трапеции: трапе-ция 1 входит в сумму (2.140) со знаком плюс, а трапеции 2 и 3 со знаком минус.
Построение отдельных составляющих h 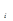 (t) осуществляется с помощью специальных таблиц переходных функций h(
(t) осуществляется с помощью специальных таблиц переходных функций h( 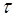 ), рассчитанных для нормированных трапеций. Нормированные трапеции имеют параметры U
), рассчитанных для нормированных трапеций. Нормированные трапеции имеют параметры U 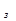 (0) = 1,
(0) = 1, 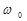 = 1, и, таким образом, каждая характеризуется одним варьируемым параметром
= 1, и, таким образом, каждая характеризуется одним варьируемым параметром 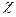 =
= 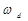 /
/ 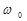 , который может иметь значение от нуля (трапеция превращается в треугольник) до единицы (трапеция превращается в прямоугольник).
, который может иметь значение от нуля (трапеция превращается в треугольник) до единицы (трапеция превращается в прямоугольник).
Для каждой составляющей характеристики находим три определяющих её пара-метра: высоту U 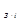 (0) и частоты
(0) и частоты 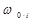 и
и 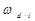 (рис.31,в). По значениям
(рис.31,в). По значениям 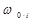 и
и 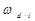 вычисляем коэффициент
вычисляем коэффициент 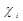 =
= 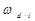 /
/ 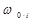 и в таблице находим соответствующую ему функцию
и в таблице находим соответствующую ему функцию 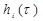 . Искомую составляющую
. Искомую составляющую 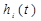 получаем из этой функции путём умножения ординат
получаем из этой функции путём умножения ординат 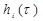 на величину
на величину 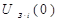 и деления абсцисс
и деления абсцисс 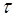 на величину
на величину 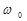 .
.
Дата добавления: 2021-04-21; просмотров: 122;










