Тогда дебит будет равен

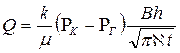.(7.24)

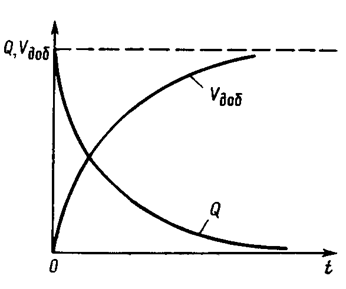Из формулы (7.24) следует, что дебит галереи убывает с течением времени по закону 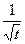и при t→ ¥ стремится к нулю.

Рис. 44

Накопленная к моменту времени t добыча V_доб определяется по формуле

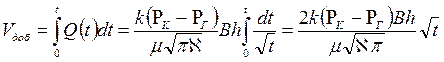
т.е. сразу после начала отбора из галереи V_доб быстро возрастает, а затем растет очень медленно.

4. Плоскорадиальный фильтрационный поток упругой жидкости; основная формула теории упругого режима

Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пласте одинаково и равно Р_К. В момент времени t=0 скважина пущена с постоянным объемным дебитом Q₀=const. В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости.

Распределение давления в пласте Р(r,t) определяется интегрированием уравнения (7.10), которое для плоскорадиального движения (в полярных координатах) запишется в виде

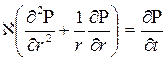. (7.25)

Начальные и граничные условия задачи:

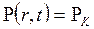при t = 0;

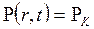при r® ¥; (7.26)

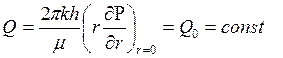при r=0, t>0.

Последнее условие запишем в виде

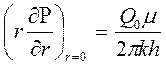. (7.27)

Проведем анализ размерностей.

Искомое распределение давления в пласте Р(r,t) зависит от пяти определяющих параметров: r, t, À, P_K , Qm/2khp , размерности которых следующие:

.

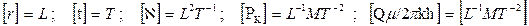Тогда давление, приведенное к безразмерному виду 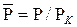зависит от двух безразмерных параметров (т.к. из пяти параметров три имеют независимые размерности – r, t, P_K: n = 5, k = 3, n-k = 2):

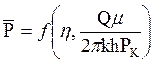, (7.28)

где 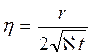- безразмерный комплекс.

Таким образом, задача автомодельна и уравнение (7.27) можно свести к обыкновенному.

Дифференцируя (7.28), найдем аналогично предыдущему

;

;

.

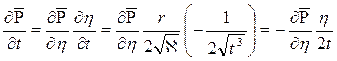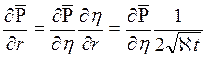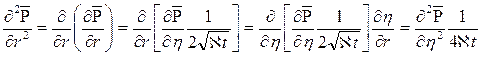Подставляя полученные выражения в уравнение (7.25), получаем обыкновенное дифференциальное уравнение вида

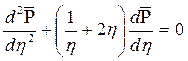, (7.29)

которое нужно проинтегрировать при условиях, полученных из (7.26) и (7.27):

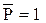при

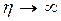
и 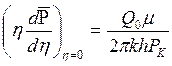. (7.30)

Используем подстановку 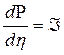, тогда вместо (7.29) будем иметь

,

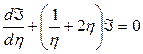или

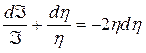. (7.31)

Интегрируя (7.31), получаем

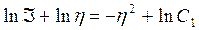, (7.32)

где С₁ – постоянная интегрирования.

Потенцируя (7.32), имеем

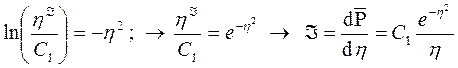. (7.33)

Интегрируя (7.33) и учитывая первое из условия (7.30), получаем

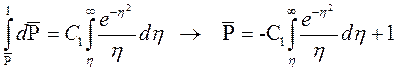. (7.34)

Умножая (7.33) на h, устремляя h® 0 и используя второе из условий (7.30), находим

.

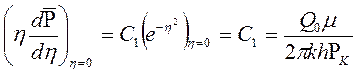Тогда из (7.34) получим

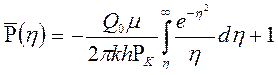. (7.35)

Интеграл в последней формуле легко свести к табличному следующей подстановкой

.

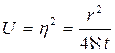Тогда .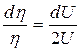

Перейдем от безразмерного давления 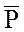к размерному 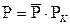, получим

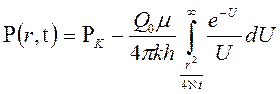. (7.36)

Интеграл в (7.36) называется интегральной показательной функцией, которая табулирована и обозначается

.

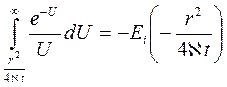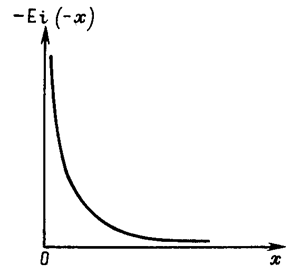Качественное изменение этой функции показано на рис. 45.

Рис. 45

Следовательно, давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется по формуле

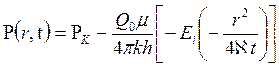. (7.37)

Формула (7.37) называется основной формулой теории упругого режима фильтрации. Она носит широкое практическое применение, и в частности используется при интерпретации результатов исследования скважин.

При малых значениях аргумента 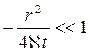- интегральная показательная функция имеет простую асимптотику:

,

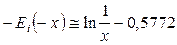где 0,5772 = ln 1,781 = С_Э – константа Эйлера;

т.е. 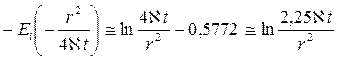; (7.38)

при этом погрешность не превышает

0,25 %, если ;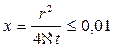

1,0 % , если .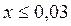

Таким образом, при малых значениях 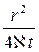, т.е. при больших значениях времени t, можно пользоваться приближенной формулой, вытекающей из (7.37) и (7.38)

,

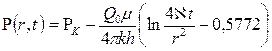или

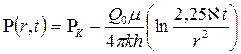. (7.39)

Из (7.37) находим, что расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соответственно по формулам

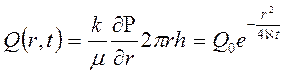; (7.40)

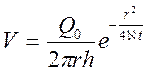. (7.41)

Из последней формулы следует, что стационарная скорость 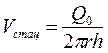достигается очень быстро на небольших расстояниях от скважины, т.к. значение коэффициента пьезопроводности À очень велико.

Заметим, что формула (7.37) справедлива лишь для точечного стока, т.е. для r = 0 в неограниченном пласте (R_K = ¥).

Для оценки влияния конечного радиуса возмущающей скважины r_C на результаты расчетов давления В.Н.Щелкачев использовал параметр Фурье 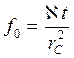. Сравнивая результаты расчетов давления по формуле (7.37) с точными данными Ван-Эвердингера и Херста, учитывающими конечный радиус скважины r_C, В.Н.Щелкачевым было показано, что для скважин обычных размеров формула (7.37) обеспечивает высокую степень точности уже на самой ранней стадии (а тем более на поздней стадии) процесса перераспределения давления.

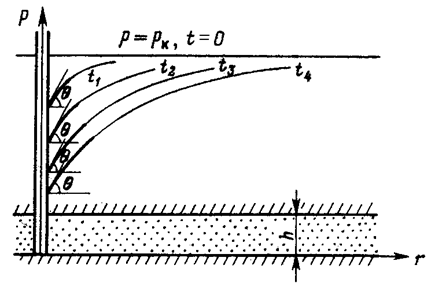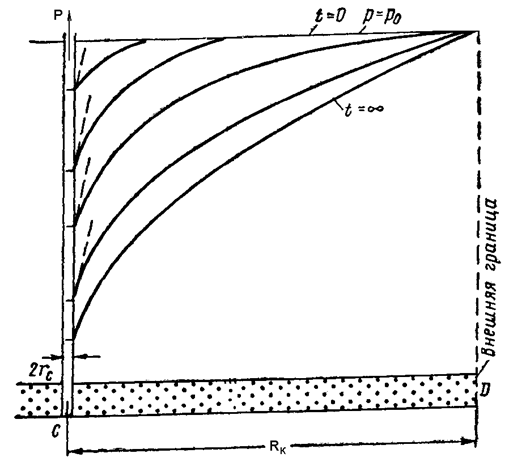
Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса r_C с постоянным дебитом Q₀ (рис.46).

Рис. 46

Для точек вблизи забоя скважины можно пользоваться формулой (7.39); дифференцируя ее по координате r, найдем градиент давления

.

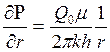Из этой формулы следует, что градиент давления для значений 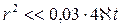практически не зависит от времени и определяется по той же формуле, что и для установившейся плоскорадиальной фильтрации несжимаемой жидкости (3.7), (3.9). Для указанных значений r пьезометрические кривые представляют собой логарифмические линии (рис.46), у которых углы наклона q касательных одинаковы для всех кривых у забоя скважины.

Таким образом, вокруг скважины, непрерывно увеличиваясь, образуется область, в пределах которой давление распределяется как при установившемся режиме (область квазиустановившегося процесса) – на рис.46 показаны жирными линиями.

Решение дифференциального уравнения упругого режима для различных случаев фильтрации упругой жидкости в ограниченных открытых и закрытых пластах представляются бесконечными рядами по функциям Бесселя. В то же время непосредственными расчетами В.Н. Щелкачев показал, что в громадном большинстве практически интересных случаев поведение возмущающей скважины в конечном открытом пласте (рис.47) можно в течении достаточно длительного времени изучать при помощи простой формулы (7.37) для бесконечного пласта. В частности расхождение в значениях 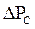для бесконечного и конечного пластов не превосходят 1%, есл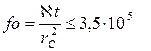и

и 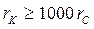или есл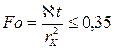и

и .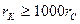

Характер распределения давления Р(r,t) для случаев ограниченного открытого и закрытого пластов показан на рис.47 и 48 соответственно.

Рис.47

Особенностью перераспределения давления в закрытом пласте (рис.48) является то, что после некоторого времени во всех точках пласта давление падает с одинаковой скоростью, о чем свидетельствует равноудаленность всех точек любой пары пьезометрических кривых.

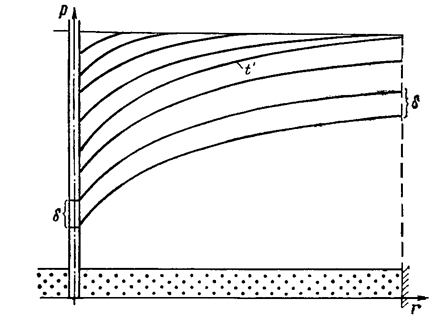
Рис. 48

5. Принцип суперпозиции в задачах упругого режима

Принцип суперпозиции (наложения) фильтрационных потоков применяется и в задачах неустановившихся процессов при упругом режиме, поскольку основное дифференциальное уравнение упругого режима (7.10) является линейным.

Сущность метода суперпозиции состоит в том, что при совместной работе нескольких добывающих и нагнетательных скважин изменение пластового давления, вызванное работой каждой из скважин, подсчитывается так, как если бы данная скважина работала одна; затем изменения давления, вызванные работой каждой скважины, алгебраически суммируются по всем скважинам. При этом скорости фильтрации в любой данной точке пласта, вызванные работой каждой скважины, суммируются геометрически.

Наличие прямолинейных границ пласта учитывается методом отображения источников и стоков, как и в случае установившейся фильтрации несжимаемой жидкости.

С помощью метода суперпозиции можно исследовать перераспределение пластового давления, вызванные пуском, остановкой или изменением темпов отбора жидкости из скважины.

Для расчета изменения пластового давления используется основная формула упругого режима фильтрации (7.37), которую можно использовать, как об этом уже было сказано ранее, с достаточно высокой степенью точности и в расчетах притока упругой жидкости к скважине конечного радиуса в открытом или закрытом конечном пласте.

Рассмотрим пример, связанный с остановкой скважины.

Предположим, что в некоторый момент времени, принимаемый за начальный (t=0), в невозмущенном пласте с давлением Р_К пущена в эксплуатацию скважина с постоянным дебитом Q и через промежуток времени t₁ остановлена. Под остановкой ее подразумевается мгновенное прекращение притока жидкости к забою скважины. Требуется определить давление в любой точке пласта в любой момент времени как при работе скважины, так и после ее остановки.

До момента времени t₁ скважина работала одна, следовательно, пластовое давление в любой точке пласта определяется по формуле (7.37)

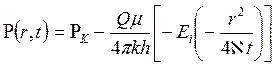, (7.42)

где t изменяется в интервале от 0 до t₁.

Начиная с момента времени t₁ (скважина уже остановлена), следуя методу суперпозиции, мысленно допустим, что вместе с продолжающей работать добывающей скважиной в той же точке начала работать нагнетательная скважина с таким же расходом Q. Следовательно, с момента t₁ в пласт в одной и той же точке закачивается столько же жидкости, сколько из него и отбирается; значит, суммарный фактический отбор жидкости из пласта оказывается равным 0, что свидетельствует об остановке добывающей скважины по условию задачи.

К моменту времени t после остановки скважины ( 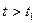) понижение давления в любой точке пласта определяется по методу суперпозиции:

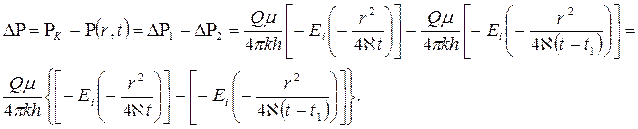
Примерный график понижения забойного давления при работе и остановке добывающей скважины показан на рис. 49.

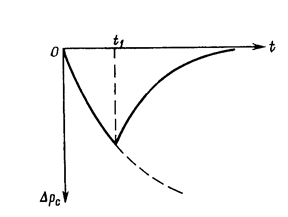Cледует заметить, что подъем давления на забое возмущающей скважины начинается сразу же после ее остановки с момента t₁. В любой другой точке пласта после момента времени t₁ будет еще некоторое время продолжаться снижение пластового давления, причем чем дальше находится эта точка пласта от возмущающей скважины, тем дольше в ней будет продолжаться процесс понижения пластового давления после остановки скважины. Затем и в этой точке пласта начинается повышение давления.

Рис. 49

6. Определение коллекторских свойств пласта по данным

исследования скважин при упругом режиме

Методы исследования пластов и скважин, основанные на изучении неустановившихся процессов изменения забойного давления в возмущающих и реагирующих скважинах, тесно связаны с теорией упругого режима. После пуска или остановки скважины на ее забое и в окружающих реагирующих скважинах возникают (в условиях упругого режима) длительные процессы перераспределения давления. При помощи самопишущих скважинных манометров можно записать повышение или понижение давления и построить график изменения забойного давления, с течением времени – кривую восстановления давления (КВД).

Чаще всего при гидродинамическом исследовании скважины наблюдают (измеряют) восстановление забойного давления после остановки скважины, ранее продолжительное время работавшей с постоянным дебитом Q.

Очевидно, что коллекторские свойства пласта влияют на форму графиков восстановления забойного давления , поэтому по форме КВД можно определить коллекторские свойства пласта – его проницаемость и пьезопроводность.

Для упрощения обработки КВД прибегают к преобразованию графиков восстановления давления, изменяя их криволинейную форму в прямолинейную.

Наиболее распространенный метод определения коллекторских свойств пласта по данным о восстановлении забойного давления в остановленных скважинах – метод построения преобразованного графика восстановления забойного давления в полулогарифмических координатах (DR, lg t), имеющего форму прямой. Прямолинейную зависимость DR от lg t установить несложно.

На основании основной формулы теории упругого режима (7.37) можно получить следующую зависимость между изменением забойного давления DR_С и временем t с момента пуска скважины в эксплуатацию с постоянным дебитом Q.

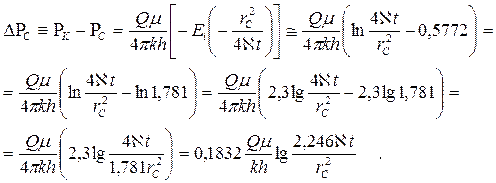
Последнее выражение можно представить в виде

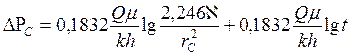, (7.43)

или

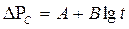, (7.44)

где

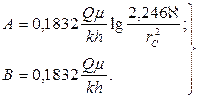(7.45)

Как видно из формул (7.43) и (7.44) изменение (снижение) забойного давления в пущенной с постоянным дебитом Q скважине оказывается линейной функцией логарифма времени. Следовательно, эти формулы можно рассматривать как уравнение графика изменения забойного давления после пуска скважины в эксплуатацию.

Рассмотрим теперь кривую восстановления забойного давления, т.е. рост забойного давления после мгновенной остановки скважины. Будем считать, что до остановки скважина длительное время работала с постоянным дебитом Q и вокруг нее в пласте имело место установившееся распределение пластового давления в соответствии с формулой (3.25)

,

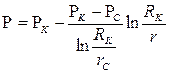т.е. пьезометрическая линия является кривой логарифмического типа.

Изменение забойного давления после мгновенной остановки скважины можно определить, используя принцип суперпозиции:

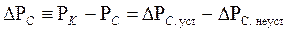, (7.46)

где DR_{С. уст} – депрессия на пласт при установившейся работе добывающей скважины с дебитом Q:

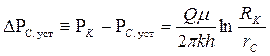; (7.47)

DR_{С. неуст} – изменение давления на забое воображаемой нагнетательной скважины, пущенной в момент t=0 с расходом Q:

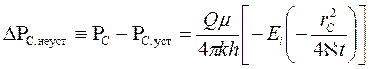. (7.48)

Так как DR_уст величина постоянная (от времени не зависит), то изменение забойного давления DR_С будет определяться по формуле (7.48), которая совпадает с формулами (7.43) и (7.44).

Обработка кривых восстановления забойного давления и определения по ним коллекторских свойств пласта проводятся следующим образом. Снятую скважинным манометром кривую восстановления забойного давления после остановки скважины перестраивают в координатах (DR_С, lg t). По прямому участку этой кривой (рис.50) находится отрезок, отсекаемый ее продолжением на оси DR_С (отрезок А), и тангенс угла наклона этой прямой к оси абсцисс (B=tg j). Затем с помощью второго равенства (7.45) определяется параметр 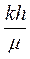, называемый гидропроводностью пласта, т.е.

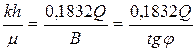. (7.49)

Если известны вязкость жидкости в пластовых условиях m и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта

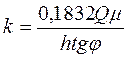. (7.50)

Далее по известному угловому коэффициенту B=tgj и радиусу скважины из первого равенства (7.45)

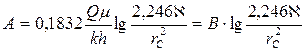
можно определить коэффициент пьезопроводности пласта

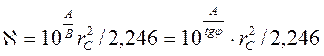. (7.51)

Отметим, что область применения указанных простых приемов интерпретации результатов исследования нефтяных скважин ограничивается условиями, при которых справедлива формула (7.37), а именно:

скважина рассматривается как источник постоянной интенсивности в бесконечном однородном пласте, и возможна мгновенная остановка притока флюида в скважину.

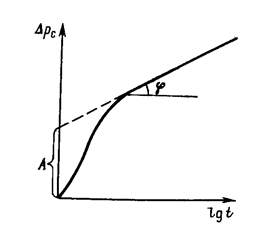График, построенный по результатам реальных промысловых исследований скважин, принимает форму прямой не сразу. На форму начальных участков графиков прослеживания забойного давления влияет изменение проницаемости в призабойной зоне пласта. В зарубежной литературе это влияние именуется «скин-эффектом» (skin – пленка, оболочка).

Рис. 50

В случае ограниченного пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД в скважине начнет искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой ограничена (рис.50). Кроме того в реальных условиях скважину нельзя остановить мгновенно. После ее закрытия на устье приток флюида из пласта продолжается еще некоторое время из-за упругости жидкости и газов, заполняющих скважину. Время выхода на асимптоту, должно очевидно превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД проявляется через значительный промежуток времени, либо даже вообще не существует.

Поскольку длительная остановка скважины нежелательна, были развиты методы определения параметров пласта на неустановившихся режимах, лишенных указанных недостатков и учитывающие, в частности, время работы скважины до ее остановки (метод Хорнера), а также приток флюида в скважину после ее остановки.