Наибольший общий делитель
Определение 3.1. Рассмотрим 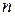 целых чисел
целых чисел 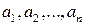 и целое число
и целое число 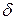 , причем
, причем 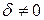 . Число
. Число 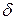 называется общим делителем чисел
называется общим делителем чисел 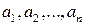 , если каждое из этих чисел делится на
, если каждое из этих чисел делится на 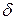 :
: 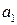

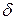 ,
, 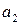

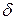 ,…,
,…, 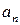

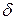 .
.
Определение 3.2. Рассмотрим 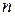 целых чисел
целых чисел 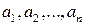 и целое число
и целое число  . Число
. Число  называется наибольшим общим делителем чисел (НОД) чисел
называется наибольшим общим делителем чисел (НОД) чисел 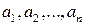 , если
, если
1)  является общим делителем чисел
является общим делителем чисел 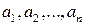 ,
,
2)  делится на любой из общих делителей чисел
делится на любой из общих делителей чисел 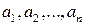 .
.
НОД чисел 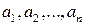 обозначают
обозначают 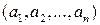 .
.
Определение 3.3. Если 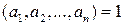 , то числа
, то числа 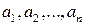 называются взаимно простыми.
называются взаимно простыми.
Свойства НОД
Теорема 3.1. НОД чисел 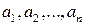 определен однозначно с точностью до знака, т. е., если числа
определен однозначно с точностью до знака, т. е., если числа 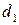 и
и 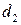 – наибольшие общие делители чисел
– наибольшие общие делители чисел 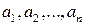 , то либо
, то либо 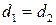 , либо
, либо 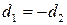 .
.
Доказательство. Из определения НОД следует, что 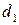

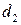 и
и 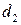

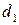 , поскольку оба этих числа являются общими делителями чисел
, поскольку оба этих числа являются общими делителями чисел 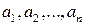 . Тогда по следствию 2 к свойству 5 делимости чисел либо
. Тогда по следствию 2 к свойству 5 делимости чисел либо 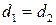 , либо
, либо 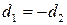 .
.
Замечание. По теореме 3.1. каждая совокупность целых чисел обладает ровно двумя НОД, отличающимися друг от друга только знаками. Поэтому можно рассматривать только случай, когда НОД чисел положителен. Далее будем считать, что 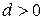 .
.
Теорема 3.2. Пусть 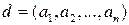 (т. е. число
(т. е. число  является наибольшим общим делителем чисел
является наибольшим общим делителем чисел 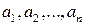 ). Тогда число
). Тогда число  является наибольшим по величине общим делителем этих чисел.
является наибольшим по величине общим делителем этих чисел.
Доказательство. Пусть 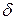 – общий делитель чисел
– общий делитель чисел 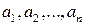 . Тогда из определения НОД следует, что
. Тогда из определения НОД следует, что 

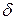 . По свойству 5 делимости чисел
. По свойству 5 делимости чисел 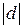
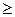
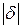 . Мы условились считать, что НОД чисел положителен, следовательно,
. Мы условились считать, что НОД чисел положителен, следовательно, 
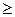
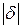 . Учитывая, что
. Учитывая, что 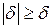 , получим требуемое утверждение.
, получим требуемое утверждение.
Теорема 3.3. Пусть 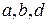 – целые числа. Для того, чтобы число
– целые числа. Для того, чтобы число  было НОД чисел
было НОД чисел  и
и  необходимо и достаточно, чтобы существовали такие взаимно простые числа
необходимо и достаточно, чтобы существовали такие взаимно простые числа 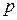 и
и 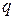 , что
, что 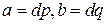 .
.
Доказательство. Необходимость. Пусть 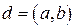 . Докажем, что существуют такие взаимно простые числа
. Докажем, что существуют такие взаимно простые числа 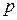 и
и 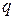 , что
, что 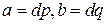 . Поскольку числа
. Поскольку числа  и
и  делятся на
делятся на  , имеем
, имеем 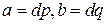 . Докажем, что числа
. Докажем, что числа 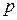 и
и 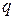 – искомые, т. е.
– искомые, т. е. 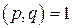 . Предположим, что это утверждение неверно, это значит, что
. Предположим, что это утверждение неверно, это значит, что 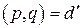 , где
, где 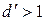 . Тогда
. Тогда 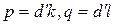 , где
, где 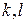 – целые числа. Следовательно,
– целые числа. Следовательно, 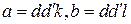 . Значит,
. Значит, 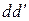 – общий делитель чисел
– общий делитель чисел  и
и  , причем
, причем 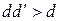 . Получили, что число
. Получили, что число  не является наибольшим общим делителем чисел
не является наибольшим общим делителем чисел  и
и  , что противоречит условию. Следовательно, сделанное нами предположение неверно, что и доказывает требуемое утверждение.
, что противоречит условию. Следовательно, сделанное нами предположение неверно, что и доказывает требуемое утверждение.
Достаточность. Пусть 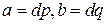 , где
, где 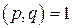 . Докажем, что
. Докажем, что 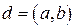 . Из условия утверждения следует, что
. Из условия утверждения следует, что 

 и
и 

 , следовательно,
, следовательно,  – делитель чисел
– делитель чисел  и
и  .
.
Предположим, что  – не является наибольшим общим делителем чисел
– не является наибольшим общим делителем чисел  и
и  . Пусть
. Пусть 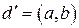 . Тогда
. Тогда 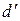

 . Это значит, что
. Это значит, что 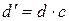 , где
, где  – целое число, причем
– целое число, причем 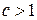 . Из определения НОД получим, что
. Из определения НОД получим, что 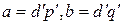 . Тогда
. Тогда 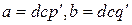 . Из единственности частного следует, что
. Из единственности частного следует, что 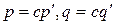 . Значит, числа
. Значит, числа 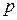 и
и 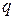 не являются взаимно простыми, что противоречит сделанному нами предположению. Полученное противоречие доказывает справедливость утверждения.
не являются взаимно простыми, что противоречит сделанному нами предположению. Полученное противоречие доказывает справедливость утверждения.
Дата добавления: 2021-02-19; просмотров: 127;










