Решение в двойных тригонометрических рядах
Аналогично решению Навье для пластины, шарнирно опертой по всем кромкам, прогиб, удовлетворяющий всем граничным условиям
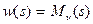
представляется в виде
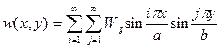 . (14.4)
. (14.4)
Подставляем (14.4) в (14.1)
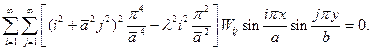 (14.5)
(14.5)
Поскольку система тригонометрических функций ортогональна в области 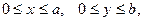 уравнение (14.5) может выполниться только в случае, когда сумма равна нулю почленно.
уравнение (14.5) может выполниться только в случае, когда сумма равна нулю почленно.
Кроме тривиального решения 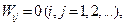 соответствующего исходной форме равновесия, отсюда следуют и нетривиальные, возможные, если равна нулю хотя бы одна из скобок. Это дает спектр собственных значений задачи
соответствующего исходной форме равновесия, отсюда следуют и нетривиальные, возможные, если равна нулю хотя бы одна из скобок. Это дает спектр собственных значений задачи
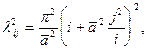 (14.6)
(14.6)
из которых нас интересует наименьшее. Очевидно, что наименьшее из 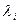 при любом фиксированном
при любом фиксированном 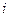 будет при
будет при 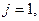 что соответствует одной полуволне в направлении, перпендикулярном сжатию. Значение же
что соответствует одной полуволне в направлении, перпендикулярном сжатию. Значение же 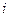 , дающее наименьшее из
, дающее наименьшее из 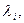 зависит от удлинения
зависит от удлинения 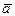 пластины. Здесь формулу (14.6) наглядней записывать в виде
пластины. Здесь формулу (14.6) наглядней записывать в виде
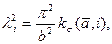
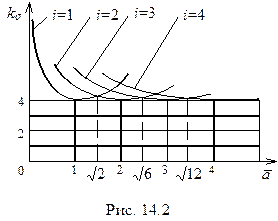
где коэффициент
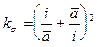 (14.7)
(14.7)
графически показан на рис.14.2.
При различных 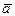 минимум обеспечивается разными
минимум обеспечивается разными 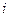 , что соответствует разному числу полуволн в направлении сжатия. Пластина теряет устойчивость с образованием квадратных впадин - выпуклостей.
, что соответствует разному числу полуволн в направлении сжатия. Пластина теряет устойчивость с образованием квадратных впадин - выпуклостей.
Приравнивая значения
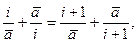
|
легко установить, что при 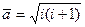 с равной вероятностью могут реализоваться как
с равной вероятностью могут реализоваться как 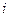 , так и
, так и 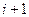
 полуволна.
полуволна.
Окончательный результат обычно записывается в виде
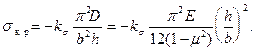 (14.8)
(14.8)
При 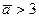 допустимо принимать
допустимо принимать
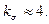
Дата добавления: 2016-09-06; просмотров: 2102;











