Метод элементарных преобразований для нахождения ранга.

Бывает лучше упростить матрицу, чтобы видеть, какие миноры равны 0 или не равны 0. Как и при вычислении определителей, можно прибавлять к строке другую строку, умноженную на число, то же самое со столбцами. Но при нахождении ранга даже больше возможных действий, чем при вычислении определителя: можно менять местами строки (столбцы), умножать строки (столбцы) на коэффициент. Соответствующие миноры в этом случае меняют знак или умножаются на с, но ведь свойство быть равными 0, либо не равными 0, от этого не меняется.

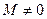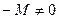Если число , то и .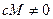

Пример.

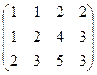
из 2-й строки вычесть 1-ю, а из 3-й удвоенную 1-ю.

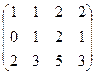
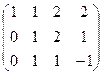
теперь из 3-й строки вычтем 2-ю 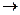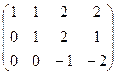. Ниже главной диагонали получились нули.

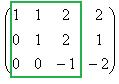
Теперь лучше видно базисный минор порядка 3. Ранг = 3. Если бы оказалось, что последняя строка состоит из нулей, то тогда был бы ответ ранг матрицы = 2.

Ранг системы векторов (количество векторов в максимальной независимой подсистеме) и ранг матрицы (порядок наибольшего невырожденного минора). На самом деле, не случайно используется одно и то же слово: если матрицу мысленно разрезать на строки, будет система векторов, и у неё ранг точно такой же, как был у исходной матрицы. Аналогичное верно и для системы столбцов. Существует такой факт:

Теорема о ранге матрицы. Ранг матрицы равен рангу системы её строк (столбцов).

Доказательство.Докажем, что если 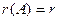, то:

1) она содержит 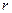линейно-независимых столбцов:

2) всякий другой столбец линейно выражается через эти 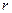столбцов.

Пусть максимальный невырожденный минор расположен в верхнем левом углу (если не так, то можно менять строки и столбцы, пока он не окажется там).

1) Докажем, что первые 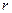столбцов образуют ЛНС векторов.

Допустим, что они линейно-зависимы. Тогда 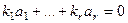, где

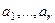- столбцы. В этом случае верно равенство с точно такими же коэффициентами и для «укороченных» столбцов минора 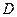, а это противоречит тому, что он невырожденный.

2) Докажем, что при добавлении любого столбца сверх указанных 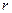, система векторов-столбцов становится линейно-зависимой.

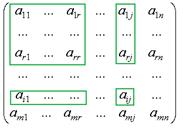
Возьмём 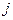-й столбец. Построим вспомогательный минор 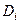порядка 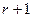, выбрав какую-либо 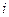-ю строку, 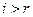. Этот минор порядка 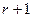, поэтому он вырожденный, так как ранг равен 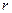. Но можно разложить его по последней строке:

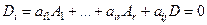
При этом 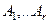не зависят от выбора строки 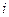, так как находятся в первых 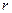строках.

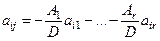
Такой определитель порядка 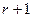можно рассматривать и при 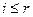, тогда последняя строка в нём - копия строки 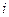, и определитель равен 0 хотя бы в силу наличия одинаковых строк. Итак, равенств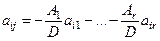о верно 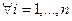. Тогда всякий 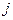-й столбец является линейной комбинацией первых 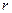столбцов. Тогда ранг системы столбцов равен .

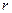(Аналогичные действия можно выполнить и со строкой i, она является линейной комбинацией первых r строк).

Следствие.Если 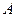квадратная матрица, то:

1) 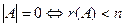, 2) .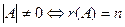

Пример. 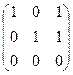здесь ранг матрицы равен 2, по крайней мере потому, что третья строка состоит из нулей. В то же самое время, если рассмотреть систему её векторов-столбцов, то видно, что третий вектор равен сумме 1-го и 2-го:

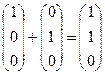
таким образом, ранг системы векторов тоже 2.

В заключение главы «матрицы и определители», рассмотрим ещё некоторые названия и определения, которые будет применяться в будущем, а также обобщение понятия 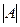на множество прямоугольных матриц.

Симметрическая матрица. ( )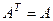

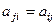Пример.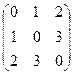

Кососимметрическая матрица. ( ) .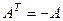

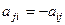Для кососимметрической матрицы, главная диагональ состоит из нулей, так как 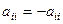то .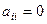

Пример. .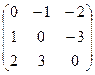

Ортогональная матрица. 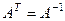. Будут рассмотрены подробнее в конце этого семестра. Это матрицы перехода от одного ортонормированного базиса к другому. Сумма квадратов элементов каждого столбца равна 1, скалярное произведение разных столбцов 0.

Пример: .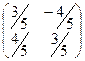

= = .

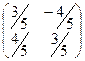
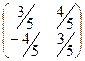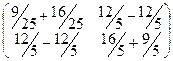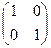Подобные матрицы. 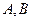подобны, если существует невырожденная матрица 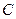, такая, что 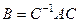, т.е. 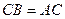. Будет изучаться в конце 2 семестра, это матрицы одного и того же линейного оператора в разных базисах.