ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ К ГЛАВЕ 4
Пример 5.1.Найдем интеграл 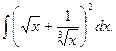
Решение. Преобразуем подынтегральную функцию и применим непосредственное интегрирование
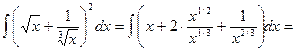
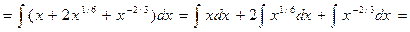
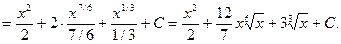
Пример 5.2.Найдем интеграл 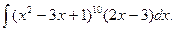
Решение. Так как производная 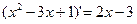 , то внесем
, то внесем 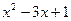 под знак дифференциала
под знак дифференциала
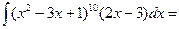
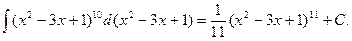
Пример 5.3.Найдем интеграл 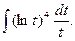
Решение. Так же как и в предыдущем примере, выражение 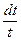 можно записать как
можно записать как 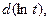 поэтому
поэтому
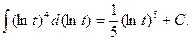
Пример 5.4.Найдем интеграл 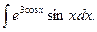
Решение. Здесь 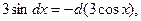 поэтому данный интеграл представляем в виде:
поэтому данный интеграл представляем в виде:
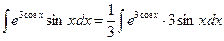 .
.
Внеся под знак дифференциала, получим
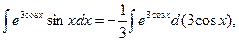
т. е. переменной интегрирования является 3соs х.
Следовательно, интеграл берется по формуле VI:
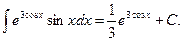
Пример 5.5.Найдем интеграл 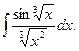
Решение. Произведем подстановку
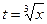 , т. е.
, т. е. 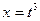 .
.
Найдем дифференциал 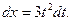
Отсюда получаем
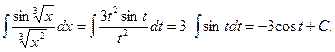
Пример 5.6.Найдем интеграл 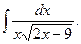
Решение. Произведем подстановку 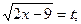 тогда
тогда 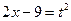 .
.
Выразим 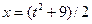 и найдем
и найдем 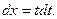
Подставив в исходный интеграл, получим
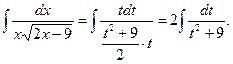
Применив формулу XVIII, получим
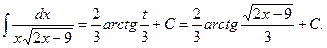
Подставив в исходный интеграл, получим Найдем интеграл 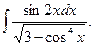
Решение. Произведем подстановку 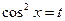 ; тогда —
; тогда — 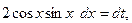 т. е.
т. е. 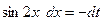 .
.
Подставив в исходный интеграл, получим 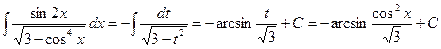
(использовали формулу XX).
Пример 5.7.Найдем интеграл 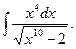
Решение. Применим подстановку 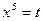 ; тогда
; тогда 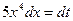 ,
, 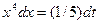 , тогда
, тогда
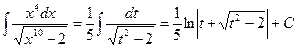
(см. формулу XXI).
Итак,
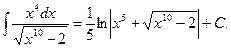
Пример 5.8. Найдем интеграл 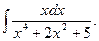
Решение. Преобразуем знаменатель дроби, выделив полный квадрат
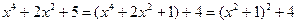 .
.
Произведем подстановку 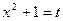 ; тогда
; тогда 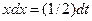 .
.
Отсюда
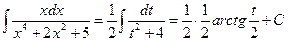 ,
,
(см. формулу XVIII).
Таким образом,
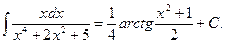
Пример 5.9. Найдем интеграл 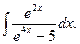
Решение. Положим 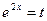 , тогда
, тогда 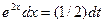 и
и
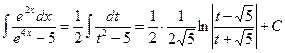
(применили формулу ХIX).
Итак,
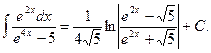
Пример 5.10. Найдем интеграл 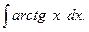
Решение.
Пусть 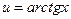 ,
, 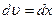 , тогда
, тогда 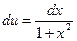 ,
, 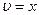 .
.
По формуле интегрирования по частям находим
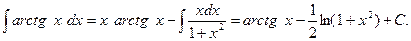
Пример 5.11. Найдем интеграл 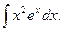
Решение. Положим 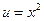 ,
, 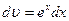 ; тогда
; тогда 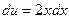 ,
, 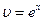 .
.
Применяем формулу интегрирования по частям:

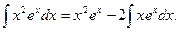
Мы добились понижения степени х на единицу.
Чтобы найти 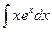 , применим еще раз интегрирование по частям.
, применим еще раз интегрирование по частям.
Полагаем 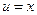 ,
, 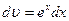 ; тогда
; тогда 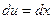 ,
, 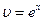
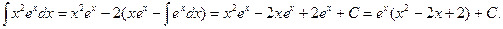
Пример 5.12. Найдем интеграл 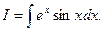
Решение. Применяем формулу интегрирования по частям.
Пусть 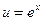 ,
, 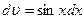 ; тогда
; тогда 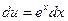 ,
, 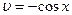 .
.
Следовательно,
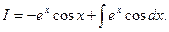
Еще раз проинтегрируем по частям.
Приняв 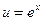 ,
, 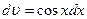 , откуда
, откуда 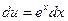 ,
, 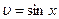 .
.
Получаем
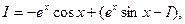 т. е.
т. е. 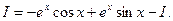
Применив дважды формулу интегрирования по частям, мы в правой части снова получили исходный интеграл. Таким образом, приходим к уравнению с неизвестным интегралом I. Из этого уравнения находим

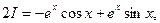 т. е.
т. е. 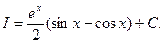
Такого вида интегралы носят название «круговые».
Пример 5.13. Найдем интеграл 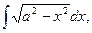 если
если 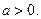
Решение. Положим 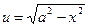 ,
, 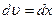 , откуда
, откуда 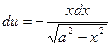 ,
, 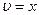 .
.
Следовательно,
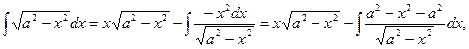
или
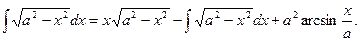
Выразим данный интеграл из полученного равенства
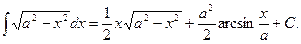
Пример 5.14. Найдем интеграл 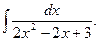
Решение. Выполним преобразование подынтегральной функции и проинтегрируем
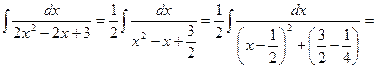
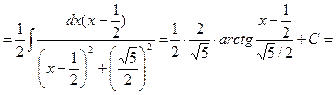
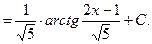
Пример 5.15. Найдем интеграл 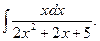
Решение. Выполним преобразование подынтегральной функции и проинтегрируем
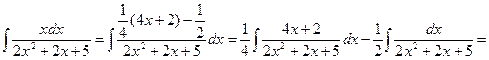
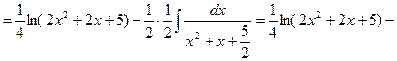
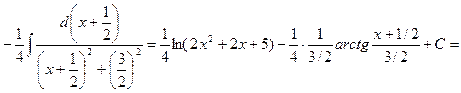
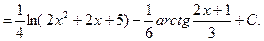
Пример 5.16. Найдем интеграл 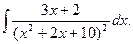
Решение. Выполним преобразование подынтегральной функции
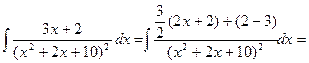
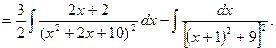
В первом интеграле произведем замену 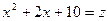 ,
, 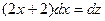 , а во втором интеграле положим
, а во втором интеграле положим 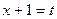 ,
, 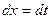 .
.
Отсюда
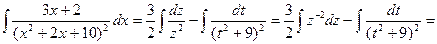
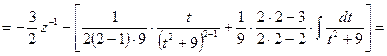
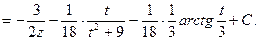
Возвращаясь к старой переменной, получаем
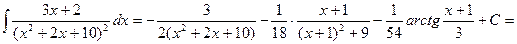
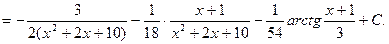
Пример 5.17. Найдем интеграл 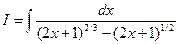
Решение. Дан интеграл от иррациональной функции 1-го вида.
Здесь 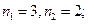 поэтому
поэтому 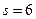 .
.
Применим подставку 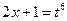 ; тогда
; тогда 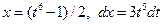 и, следовательно,
и, следовательно,
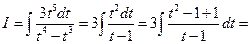
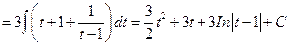
Возвратимся к старой переменной. Так как 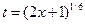 , то
, то
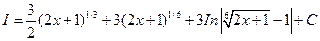
Пример 5.18. Найдем интеграл 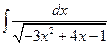 .
.
Решение. Данный интеграл от иррациональной функции 2-го вида. Преобразуем подкоренное выражение и внесем под знак дифференциала:
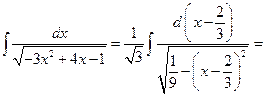
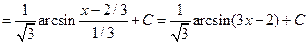
Пример 5.19. Найдем интеграл 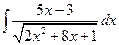 .
.
Решение. Выделим в числителе производную подкоренного выражения:
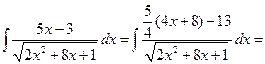
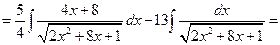
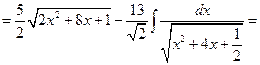
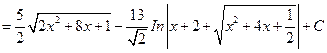
Пример 5.20. Найдем интеграл 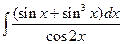 .
.
Решение. Дан интеграл от тригонометрической функции.
Так как подынтегральная функция нечетна относительно синуса, то полагаем 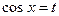 .
.
Отсюда 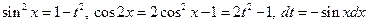 .
.
Таким образом,

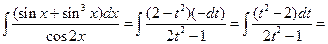
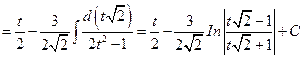 .
.
Следовательно,
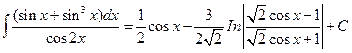 .
.
Пример 5.21. Найдем интеграл 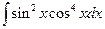 .
.
Решение. Дан интеграл от тригонометрической функции. Применим формулу (3)
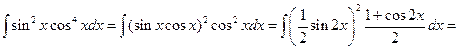
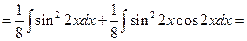
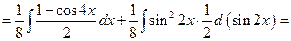
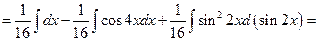
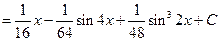 .
.
Пример 5.22. Найдем интеграл 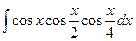
Решение. Применим к произведению 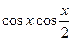 формулу (2):
формулу (2):
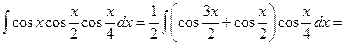
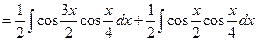
Снова используя ту же формулу, находим
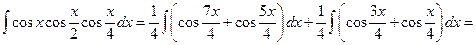
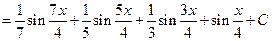
Дата добавления: 2020-10-25; просмотров: 141;










