Поле комплексных чисел

Поле комплексных чисел

Еще в древности при решении задач встречались случаи, связанные с комплексными корнями уравнений. В таких случаях считали задачу неразрешимой. Упорством, достойным подражания, в истории математикиотмечена борьба сторонников и противников «мнимых» чисел, источником которых служит уравнение х²+1=0. Можно было бы ограничиться формальной записью решения в виде ±Ö-1. Но такое немудрено было сделать и в более далекие времена, оставалось лишь придать этой записи смысл. Первые попытки введения в математику комплексных чисел были сделаны итальянскими математиками XVI века Кардано и Бомбелли в связи с решением уравнений 3 и 4 степени. Математики того времени использовали различные термины для названия новых чисел: «мнимые», «невозможные», «воображаемые» и т.д. и применяли к ним те же правила действий, которым подчинялись действительные числа. Однако смысл новых чисел оставался неясным, что нашло отражение в терминологии. Кардано называл эти числа «ложными», «поистине софистическими числами». Первое формальное обоснование действий с комплексными числами дано в алгебре итальянского математика Бомбелли (1572 г.). Но лишь в XIX веке Гауссу удалось достаточно убедительно обосновать понятие комплексного числа.

Поле комплексных чисел

Рассмотрим множество упорядоченных пар действительных чисел

С={a½a=(a,b), a,bÎÂ}.

Введем на этом множестве две операции следующим образом:

"a,bÎС (a=(a₁,b₁), b=(a₂,b₂)),

сложение a+b=(a₁+a₂, b₁+b₂) и умножение ab=(a₁a₂-b₁b₂, a₁b₂+a₂b₁). Из определения упорядоченных пар следует (a=bÛ(a₁,b₁)=(a₂,b₂)Û .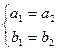

Теорема. Алгебра (С,+,×) – поле.

Доказательство

Для доказательства проверим выполнимость всех аксиом поля. Аксиомы А0 и МО выполняются по определению операций, так как в результате снова получается упорядоченная пара действительных чисел. Аксиомы А1, А1’ выполняются, так как сложение действительных чисел ассоциативно и коммутативно. Действительно,

пусть a,b,gÎС Û a=(a₁,b₁), b=(a₂,b₂), g=(a₃,b₃), тогда a+(b+g)= (a₁,b₁)+(a₂+a_3,b₂+b₃)=(a₁+(a₂+a₃)_,b₁+(b₂+b₃))=((a₁+a₂)+a₃)_,(b₁+b₂)+b₃)=(a+b)+g.Аналогично легко проверяется коммутативность сложения. (Проверить самостоятельно.) Очевидно, что роль 0 выполняет пара (0,0). Действительно, "aÎС(a=(a₁,b₁), тогда a+0=(a₁,b₁)+(0,0)= (0,0)+(a₁,b₁)=0+ a= a. Пусть aÎС, тогда a=(a₁,b₁), где а₁,.b₁ÎÂ но тогда -а₁,.-b₁ÎÂ, следовательно, (-а₁,.-b₁)=-aÎK. Таким образом, аксиома А2 выполняется. Проверим аксиому М1. Пусть a,b,gÎСÛa=(a₁,b₁), b=(a₂,b₂), g=(a₃,b₃), тогда

a(bg) = (a₁,b₁)(a₂a₃-b₂b₃,a₂b₃+a₃b₂) = (a₁(a₂a₃-b₂b₃),b₁(a₂b₃+a₃b₂)) =

= (a₁a₂a₃-а₁b₂b₃,b₁a₂b₃+b₁a₃b₂)); (ab)g = (a₁a₂-b₁b₂,a₁b₂+a₂b₁)(a₃,b₃) =

=((a₁a₂-b₁b₂)a₃-(a₁b₂+a₂b₁)b₃,(a₁b₂+a₂b₁)a₃+(a₁a₂-b₁b₂) b₃)=

=(a₁a₂a₃-а₁b₂b₃,b₁a₂b₃+b₁a₃b₂)), то есть a(bg)=(ab)g,

следовательно, аксиома М1 выполняется. Самостоятельно проверить аксиому коммутативности умножения. Роль единицы выполняет пара (1,0). Действительно,

"aÎС(a=(a,b), тогда aе=(a,b)(1,0)= (a×1-b×0,b×1+a×0)=(a,b)= a.) Найдем обратный элемент. Пусть aÎС(a=(a,b)) обозначим a^-1=(x,y), будем искать х и у исходя из определения обратного элемента, то есть

aa^-1=е Û (a,b)(x,y)=(ax-by,ay+bx)=(1,0) Û Ù ay+bx=0 Û

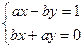
Получили систему из двух линейных уравнений с двумя неизвестными. Решив эту систему, получим

a^-1=( 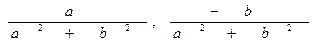)ÎС,

следовательно, аксиома М2 выполняется. Самостоятельно проверить аксиому D. Получили, что С – поле.

Определение. Поле С называется полем комплексных чисел, а его элементы – комплексными числами.

Теорема. Поле С содержит подполе, изоморфное полю действительных чисел.

Доказательство

Рассмотрим множество Р={a½a=(а,0), где аÎÂ}. Очевидно, что РÌС. Самостоятельно доказать, что Р - подполе поля С. Устанавливаем соответствие между множествами Р и  следующим образом: "аÎÂ(j(а)=(а,0)ÎС). Это отображение биекция, так как каждому действительному числу соответствует единственный элемент множества Р и, наоборот, каждый элемент множества Р соответствует одному и только одному действительному числу. Покажем, что это отображение сохраняет операции. Пусть a,bÎÂ, j(a)=(a,0), j(b)=(b,0), тогда

j(a+b) =(a+b,0), j(ab) =(ab,0), j(a)+ j(b)=(a,0)+(b,0)=(a+b,0+0)=(a+b,0),

j(a) j(b)=(a,0)(b,0)=(ab-0,a0+b0)=(ab,0)

Обе операции сохраняются. Теорема доказана.

Таким образом, с точностью до изоморфизма можем считать, что поле действительных чисел является подполем поля комплексных чисел.

Так как в любом упорядоченном поле "аÎР(а²³0), а в поле комплексных чисел i ²=-1, то поле комплексных чисел нельзя упорядочить.