НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ

С проблемой нахождения собственных значений встречаются во многих научно-технических задачах. Например, в теории колебаний собственные значения – это собственные частоты колебаний системы, в спектроскопии по собственным значениям определяют компоненты газов, в вычислительной математике некоторые исследования требуют нахождения собственных значений и т.д.

Все эти конкретные проблемы сводятся к одной и той же задаче вычисления собственных чисел квадратной матрицы с действительными или комплексными элементами.

Рассмотрим квадратную матрицу A = {a_ij}, i, j = 1…n. Если эта матрица переводит вектор х¹ 0 в коллинеарный ему вектор lх:

Ах = lх, (4.18)

то вектор х называется собственным вектором матрицы А, а l – собственным числом матрицы А, соответствующим данному собственному вектору х.

Таким образом, собственные векторы матрицы А являются ненулевыми решениями матричного уравнения (4.18), или

Сх = 0, (4.19)

где матрица С = (А–lЕ) называется характеристической матрицей данной матрицы А:

.

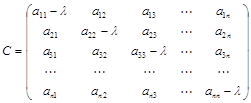Система (4.19) имеет ненулевые решения лишь тогда, когда определитель матрицы С равен нулю: det (A–lE) = 0.

Раскрывая этот определитель, получаем полином n-ой степени относительно l с единичным коэффициентом при старшей степени – характеристический полином

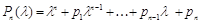. (4.20)

Таким образом, процесс нахождения собственных значений матрицы можно свести к следующим действиям:

1) построение характеристического полинома, то есть нахождение его коэффициентов p₁, …, p_n;

2) нахождение n корней характеристического полинома l_j,

j = 1,.., n, которые составляют так называемый спектр матрицы.

Если ранг матрицы С равен r (r<n), то существует k=n–r линейно независимых собственных векторов x^(1,j), x^(2,j),…, x^(k,j), отвечающих корню l_j.

Можно доказать, что число линейно независимых собственных векторов, отвечающих одному и тому же корню характеристического уравнения не превышает кратности этого корня. Отсюда, в частности, следует, что если корни характеристического уравнения различны, то каждому собственному значению соответствует с точностью до коэффициента пропорциональности один и только один собственный вектор.

Метод Леверрье

Рассмотрим один из способов определения коэффициентов характеристического полинома – метод Леверрье. Он основан на использовании формулы Ньютона для суммы степеней корней алгебраического уравнения.

Пусть l₁, l₂,…, l_n – корни полинома (4.20).

Обозначим 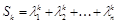(k = 1, …, n).

Тогда для любого k £ n справедлива формула Ньютона [2]

.

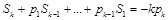Отсюда для k = 1,…, n получаем уравнения для нахождения коэффициентов характеристического полинома

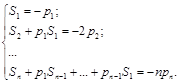(4.21)

Осталось только определить суммы S₁, S₂, … , S_n. Известно, что

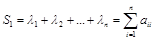– сумма диагональных элементов матрицы (след матрицы[3], tr A, или Sp A);

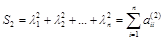– сумма диагональных элементов матрицы А², полученной возведением в квадрат матрицы А;

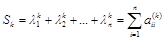и так далее.

Таким образом, порядок действий следующий:

1) простым перемножением вычисляем степени данной матрицы А², А³, … , Аⁿ ;

2) находим их следы – суммы диагональных элементов S₁, S₂, …, S_n;

3) по рекуррентным формулам (4.21) находим искомые коэффициенты p₁, p₂,…, p_n;

4) после получения характеристического полинома ищем его корни l₁, l₂, …, l_n одним из способов, которые будут рассмотрены в главе 5.