Различные способы задания прямой
Пусть 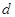 - прямая в пространстве, точка
- прямая в пространстве, точка 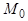 - некоторая точка этой прямой. Любой ненулевой вектор
- некоторая точка этой прямой. Любой ненулевой вектор 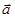 , параллельный этой прямой, называется ее направляющимвектором .
, параллельный этой прямой, называется ее направляющимвектором .
Ясно, что прямая имеет бесконечное множество направляющих векторов, любые два из которых коллинеарны.
Тогда 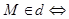 векторы
векторы 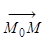 и
и 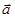 коллинеарны:
коллинеарны:
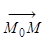 =
= 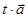 , где
, где 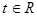 (1)
(1)
Таким образом, чтобы задать прямую 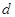 достаточно задать ее точку
достаточно задать ее точку 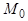 и направляющий вектор
и направляющий вектор 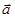 .
. 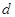 =
= 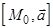 .
.
Формула(1) устанавливает взаимно однозначное соответствие между точками прямой 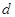 и значением параметра
и значением параметра 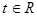 . Параметр
. Параметр 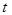 является координатой точки
является координатой точки 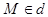 в системе координат
в системе координат 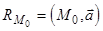 на прямой
на прямой 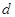 .
.
Возьмем какую-либо аффинную систему координат 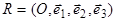 в пространстве, и пусть относительно ее точки
в пространстве, и пусть относительно ее точки 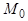 и
и 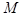 имеют координаты
имеют координаты
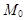
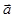
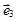 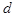
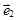 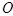
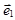
| 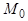 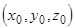 , , 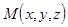 . Вектор . Вектор 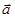 разложим по векторам базиса разложим по векторам базиса 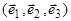 : :
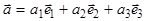 .
Сравнивая одноименные координаты векторов в формуле (1), получим: .
Сравнивая одноименные координаты векторов в формуле (1), получим:
|
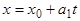 ,
,
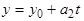 , (2)
, (2)
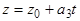 .
.
Обратно (2) 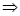 (1). Таким образом , уравнения (2) определяют прямую
(1). Таким образом , уравнения (2) определяют прямую 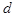 в пространстве. Они называются параметрическимиуравнениямипрямой.
в пространстве. Они называются параметрическимиуравнениямипрямой.
2. Если 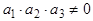 , то исключая
, то исключая 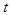 из уравнений (2), получим
из уравнений (2), получим 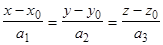 (3).
(3).
Если одна из координат направляющего вектора 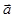 прямой
прямой 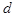 равна нулю, например,
равна нулю, например, 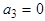 , то
, то
(2) 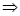
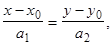
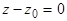
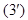
    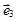 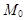
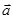
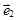 d d
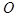
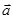 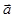
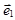 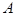
| В этом случае прямая 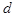 параллельна плоскости параллельна плоскости 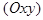 ( в частности ( в частности 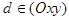 . Действительно, пусть . Действительно, пусть 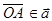 , тогда , тогда 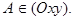 Так как Так как 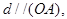 то то 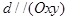 . .
|
Если две координаты направляющего вектора 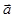 прямой
прямой 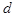 равны нулю, например,
равны нулю, например, 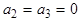 , то
, то 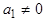 и
и
(2) 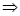
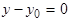 ,
, 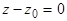
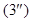
В этом случае прямая 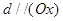 , в частности
, в частности 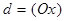 .
.
Уравнения (3), 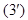 ,
, 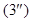 называются каноническимиуравнениями прямой.
называются каноническимиуравнениями прямой.
3. Прямая 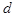 будет определена, если задать две её различные точки
будет определена, если задать две её различные точки 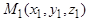 и
и 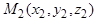 . Вектор
. Вектор 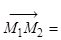
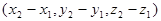 служит направляющим вектором этой прямой.
служит направляющим вектором этой прямой.
Уравнения прямой 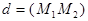 можно записать в виде (2) и (3):
можно записать в виде (2) и (3):
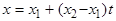
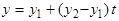 ,
,
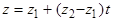 и
и
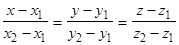 ,
, 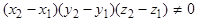 .
.
4. Прямая 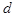 может быть задана как линия пересечения двух плоскостей
может быть задана как линия пересечения двух плоскостей 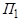 и
и 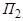 :
: 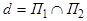 . Пусть в аффинной системе координат
. Пусть в аффинной системе координат 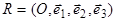 плоскости
плоскости 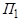 и
и 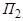 определяются уравнениями:
определяются уравнениями:
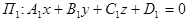 ,
, 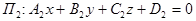 (4)
(4)
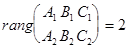 (условие пересечения
(условие пересечения 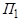 и
и 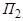 )
)
Система уравнений (4) определяет прямую 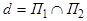 . Координаты
. Координаты 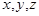 точки
точки 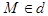 являются решением системы уравнений (4).
являются решением системы уравнений (4).
Если 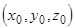 - какое -либо решение системы (4) то эта система равносильна системе уравнений
- какое -либо решение системы (4) то эта система равносильна системе уравнений
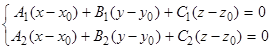
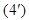
Общее решение системы 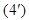 имеет вид:
имеет вид:
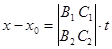 ,
, 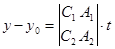 ,
, 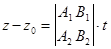
Отсюда 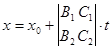 ,
, 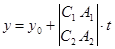 ,
, 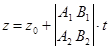 (5)
(5)
Уравнения (5) являются параметрическими уравнениями прямой 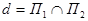 . Направляющий вектор
. Направляющий вектор 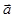 прямой
прямой 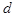 имеет координаты:
имеет координаты:
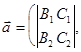
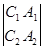
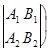 (определенные с точностью до общего множителя
(определенные с точностью до общего множителя 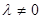 ).
).
В прямоугольной системе координат 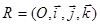
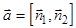 ,где
,где 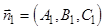
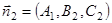 - векторы нормалей плоскостей
- векторы нормалей плоскостей 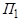 и
и 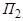 соответственно
соответственно 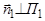 ,
, 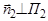 ).
).
§14. Взаимное расположение прямой и плоскости.
Пусть имеем прямую d, заданную уравнениями
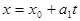
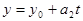 (1)
(1)
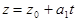
и плоскость П, заданную уравнением:
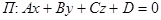 (2)
(2)
относительно аффинной системы координат 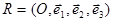 . Будем искать общие точки прямой d и плоскости П. Для этого нужно решить систему уравнений (1) и (2). Заменяя х, у, z в уравнении (2) по формулам (1), получим:
. Будем искать общие точки прямой d и плоскости П. Для этого нужно решить систему уравнений (1) и (2). Заменяя х, у, z в уравнении (2) по формулам (1), получим:
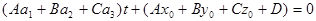 (3)
(3)
Здесь возможны случаи:
1) 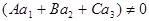 (4) <=> система уравнений (1), (2) имеет единственное решение. Таким образом, условие (4) является необходимым и достаточным условием пересечения прямой d и плоскости П . В прямоугольной системе координат
(4) <=> система уравнений (1), (2) имеет единственное решение. Таким образом, условие (4) является необходимым и достаточным условием пересечения прямой d и плоскости П . В прямоугольной системе координат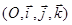 оно имеет простой геометрический смысл: скалярное произведение
оно имеет простой геометрический смысл: скалярное произведение 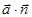 направляющего вектора
направляющего вектора 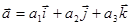 прямой d и вектора нормали
прямой d и вектора нормали 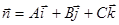 плоскости П отлично от нуля. Следовательно, векторы
плоскости П отлично от нуля. Следовательно, векторы 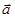 и
и 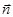 не ортогональны.
не ортогональны.
В частности, прямая d перпендикулярна плоскости П тогда и только тогда, когдавекторы 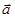 и
и 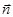 коллинеарны, т.е. когда
коллинеарны, т.е. когда
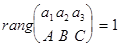
2. 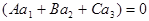 ,
, 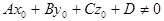 (5)
(5)
Следовательно, уравнение (3) не имеет решений, а, значит, и система (1),(2) не имеет решения. Таким образом, условия (5) являются необходимыми и достаточными условиями того, что 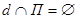 (прямая и плоскость параллельны).
(прямая и плоскость параллельны).
В прямоугольной системе координат они означают, что
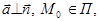 где
где 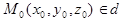 .
.
3) 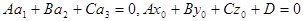 (6)
(6)
Уравнение (3) удовлетворяется любым значением t, а, значит, система (1), (2) имеет бесконечное множество решений. Следовательно, условия (6) являются необходимыми и достаточными для того, чтобы прямая d принадлежала плоскости II.
В прямоугольной системе координат они означают, то что 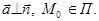
Из соотношений (5), (6) заключаем, что
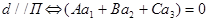
§15. Взаимное расположение двух прямых
в пространстве
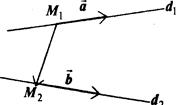
Пусть имеем две прямые 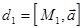 ,
, 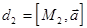 каждая из которых задана точкой и направляющим вектором с координатами:
каждая из которых задана точкой и направляющим вектором с координатами:
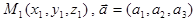 ,
, 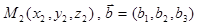
относительно аффинной системы координат 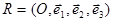 .
.
|
Обозначим:
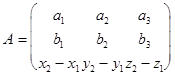 ,
,
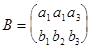 ,
, 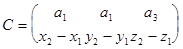
1) Векторы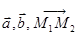 - некомпланарны <=> rangA=3, значит detA ¹0. Следовательно, прямые
- некомпланарны <=> rangA=3, значит detA ¹0. Следовательно, прямые 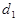 и
и 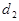 скрещиваются.
скрещиваются.
2) Векторы 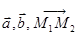 - компланарны
- компланарны 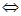 rangA=2, т.е. det À = 0. Следовательно, прямые
rangA=2, т.е. det À = 0. Следовательно, прямые 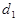 и
и 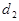 лежат в одной плоскости.
лежат в одной плоскости.
а) векторы 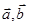 - неколлинеарны
- неколлинеарны 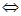 rangB = 2. Тогда прямые
rangB = 2. Тогда прямые 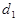 и
и 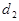 пересекаются.
пересекаются.
б) векторы 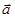 и
и 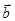 - коллинеарны,
- коллинеарны, 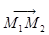 и
и 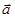 - неколлинеарны
- неколлинеарны 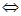 rangB = 1, rangC = 2. При этом прямые
rangB = 1, rangC = 2. При этом прямые 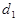 и
и 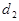 параллельны.
параллельны.
3) Векторы 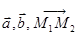 коллинеарны
коллинеарны 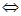 rangB = 1, rangC =1
rangB = 1, rangC =1 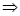 rangА = 1. Следовательно, прямые
rangА = 1. Следовательно, прямые 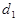 и
и 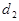 совпадают.
совпадают.
Дата добавления: 2020-10-25; просмотров: 178;










