Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы

Пусть в векторном пространстве V заданы два базиса e = {e₁, e₂, …, e_n} и f = {f₁, f₂, …, f_n}. Пусть A(e) = (а_ij) и A(f) = (b_ij) – матрицы билинейной формы A в указанных базисах.

Теорема 11.1.Матрицы A(e) и A(f) билинейной формы A(x, y) в базисах {e} и {f} связаны соотношением

A(f) = C^t×A(e)×C, (*),

где C – матрица перехода от базиса {e} к базису {f}, а C^t –транспонированная матрица C.

Следствие. Ранг матрицы A(f) равен рангу матрицы A(e).

Это утверждение следует из равенства (*): так как С – матрица перехода от одного базиса к другому, то матрица С и матрица C^t– невырожденные, поэтому умножение на них матрицы A(e) не меняет ее ранга.

Определение 11.4. Рангом билинейной формы, заданной в конечномерном векторном пространстве V , называется ранг матрицы этой формы в произвольном базисе пространства V.

Определение 11.5. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

Квадратичные формы

Пусть A(x, y) – симметрическая билинейная форма, заданная на векторном пространстве V.

Определение 11.6.Квадратичной формой называется числовая функция одного векторного аргумента x, которая получается из билинейной формы A(x, y) при x = y.

Определение 11.7.Симметрическая билинейная форма A(x, y) называется полярной квадратичной форме A(x, x).

Пусть дана билинейная форма A(x, y) = 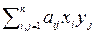, положим в ней x_i = y_j, тогда мы получим представление квадратичной формы A(x, x) в конечномерном векторном пространстве V с заданным базисом {e}:

A(x, x) = 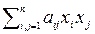. (2)

Определение 11.8.Матрица (a_ij) называется матрицей квадратичной формы A(x, x) в заданном базисе {e}.

При переходе к новому базису матрица квадратичной формы преобразуется по формуле A(f) = C^t×A(e)×C и ранг этой матрицы не меняется при переходе к новому базису.

Определение 11.9. Ранг матрицы квадратичной формы A(x, x) называется рангом квадратичной формы.

Определение 11.10. Квадратичная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

Определение 11.11. Квадратичная форма A(x, x) называется

1. Положительно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) > 0.

2. Отрицательно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) < 0.

3. Знакопеременной, если существуют такие x и y, что A(x, x) > 0 и A(y, y) < 0.

4. Квазизнакоопределенной, если для всех x, A(x, x) ≥ 0 (или A(x, x) ≤ 0) и имеется вектор x ≠ 0, для которого A(x, x) = 0.

Замечание. Если A(x, y) – билинейная форма, полярная положительно определенной квадратичной форме A(x, x), то A(x, y) удовлетворяет аксиомам скалярного произведения векторов в евклидовом пространстве:

1) A(x, y) = A(y, x) – в силу симметричности A(x, x).

2) A(x + y, z) = A(x, z) + A(y, z) – в силу определения билинейной формы.

3) A(λx, y) = λA(x, y) – в силу определения билинейной формы.

4) A(x, x) ≥ 0 и A(x, x) > 0 при х ≠ 0, т. к. A(x, x) положительно определена.

Вывод. Скалярное произведение в векторных пространствах может быть задано с помощью билинейной формы:

(x, y) = 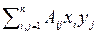= A(x, y).