Матрицы линейного оператора в различных базисах

Зададим в пространстве V два базиса e₁, e₂, …, e_n и e'₁, e'₂, …, e'_n (старый и новый). Связь между двумя базисами выражается матрицей перехода T . В пространстве V действует линейный операторj.В каждом из этих базисов для линейногооператоранайдены матрицы. Обозначим их, соответственно, M(j)и M'(j) иустановим, как одна из них выражается через другую.

Пусть [x] и [x]' столбцы координат произвольного вектора x в старом и новом базисах соответственно, связь между которыми дает формула: [x] = Т×[x]'. Векторj(x) – образ вектора х, пусть [j(x)] и [j(x)]' – столбцы координат вектораj(x) в старом и новом базисах соответственно.Имеет место формула [j(x)] = Т×[j(x)]'.

Вставим в соотношение [j(x)] = M(j)×[x] выражение старыхкоординатвекторов x и j(x) черезновые: Т×[j(x)]' = M(j)×Т×[x]'. Умножим полученное равенство слева на матрицу T ^–1 и получим [j(x)]' = (T ^–1×M(j)×Т )×[x]'.

Изтеоремы 9.2 о матрице линейного оператора следует, что

M '(j) = T ^–1×M(j)×Т .

Пример 9.3. 1) Линейный операторjв базисе e₁, e₂ задан формулой j(x) = (3х₁ – х₂, х₁ + х₂). Найти матрицу этого линейногооператора в базисе e'₁, e'₂ если e'₁ = 3е₁ + 2е₂, e'₂ = 4е₁ + 3е₂.

Решение. Сначала составим матрицу линейногооператора в старом базисе, для чего нужны координаты образов базисных векторов:

j(e₁) = j(1, 0) = (3×1 – 0, 1 + 0) = (3, 1),

j(e₂) = j(0, 1) = (3×0 – 1, 0 + 1) = (–1, 1),

M(j) = .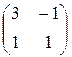

Затем находим матрицу перехода T и обратную к ней матрицу T ^–1:

e'₁ = 3е₁ + 2е₂ Þ e'₁ = (3, 2),

e'₂ = 4е₁ + 3е₂ Þ e'₂ = (4, 3),

T = 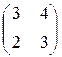тогда T ^–1 = .

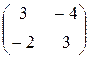Используем формулу и находим M '(j) = T ^–1×M(j)×Т :

M '(j) = × × = × = .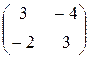

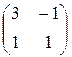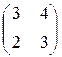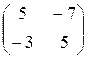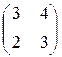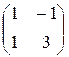Ответ: M '(j) = .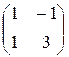

2) Линейный операторjв базисе e₁, e₂ задан формулой j(x) = (2х₁ + 4х₂, –х₁ – 3х₂). Найти матрицу этого линейногооператора в базисе e'₁, e'₂ если e'₁ = –4е₁ + е₂, e'₂ = –е₁ + е₂.

Решение. Порассмотренному алгоритму найдем M(j) и M '(j).

Ответ: M(j) = 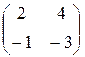, M '(j) = .

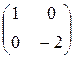Отметим, что в новом базисе матрица линейного оператора приняла диагональный вид.

Подобные матрицы

Рассмотрим множество Р^n´n квадратных матриц порядка n с элементами из произвольного поля P.

Введем на этом множестве отношение между матрицами – отношение подобия.

Определение 9.4. Матрица A называется подобной матрице B, если существует обратимая матрица T такая, что А = T ^–1×B×T.Обозначение А ~ B.