Ортогональное дополнение подпространства
V – евклидово векторное пространство, L – его подпространство.
Определение 8.23. Говорят, что вектор а ортогонален подпространству L , если вектор а ортогонален любому вектору из подпространства L, т. е.
а ^ L Û а ^ х, " х Î L.
Определение 8.24. Ортогональным дополнением подпространства L называется множество L* всех векторов, ортогональных подпространству L, то есть L* = {x | x ^ L}.
Теорема 8.13. Ортогональное дополнение подпространства является подпространством.
Теорема 8.14. Прямая сумма подпространства L и его ортогонального дополнения L* равна пространству V, т. е. L Å L* = V.
Пример 8.13. Найти ортогональное дополнение подпространства L, натянутого на векторы а1 = (1, 1, 1, 1), а2 = (–1, 1, –1, 1), а3 = (2, 0, 2, 0).
Решение. Для того чтобы вектор x был ортогонален подпространству, необходимо и достаточно, чтобы он был ортогонален векторам системы образующих этого подпространства. Пусть х = (х1, х2, х3, х4), запишем условие ортогональности этого вектора векторам а1, а2, а3: (х, а1) = 0, (х, а2) = 0, (х, а3) = 0. В координатной форме эти условия представляют собою однородную систему линейных уравнений: 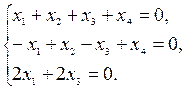 Множество решений этой системы представляет собою подпространство L*, ортогональное подпространству L.
Множество решений этой системы представляет собою подпространство L*, ортогональное подпространству L.
Решая систему, получим фундаментальный набор решений:
с1 = (–1, 0, 1, 0), с2 = (0, –1, 0, 1). Эти векторы образуют базис множества решений системы, то есть базис L*, т. о. L* = L(с1,с2), dim L* = 2.
Линейные операторы
9.1. Основные понятия и способы задания линейныхоператоров
Дано V – векторное пространство над полем P, dim V = n.
Определение 9.1. Говорят, что задано отображение j множества V в себя, если каждому элементу x из V поставлен в соответствие единственный элемент y, тоже принадлежащий V. При этом приняты следующие обозначения и термины: j: V ® V, j: х ® y, j(х) = y; элемент x – прообраз элемента y, y – образ x.
Определение 9.2. Линейным оператором пространства V называется отображение j: V ® V такое, что " a, b Î V, " l Î Р
1) j(a + b) = j(a) + j(b),
2) j(la) = lj(a).
Вместо «линейный оператор» говорят также «линейное отображение» или «отображение, сохраняющее операции сложения и умножения на элемент поля»
Пример 9.1. 1) В произвольном векторном пространстве V зададим отображение следующей формулой: j(х) = kх. Это отображение является линейным оператором и называется оператором гомотетии.
Если k =1, то отображение примет вид: j(х) = 1. Его называют тождественным оператором и обозначают буквой e: e(х) = х.
Если k = 0, то получают нулевой оператор q: q(х) = o.
2) В пространстве V = R2´2 оператор транспонирования задают формулой j(А) = Аt, где Аt – матрица, транспонированная для матрицы А.
3) В пространстве V = R[x](£n) (многочленов степени, не превосходящей n) можно задать отображение j, ставящее в соответствие произвольному многочлену его производную, т. е. j: f(x) ® f '(x),j(f ) = f '. Покажем, что это отображение линейно:
j(f + g) = (f + g)' = f ' + g ' = j(f ) + j(g),
j(lf ) = (lf )' = l(f )' = lj(f ).
Способы задания линейныхоператоров
Приведенные примеры не показывают, сколько в каждом векторном пространстве существует линейных операторов, каким способом их можно задавать.Ответом на эти вопросыявляется следующая теорема.
Теорема 9.1. Для того чтобы задать линейный оператор, достаточно задать образы базисных векторов.
Доказательство. Другими словами, если e1, e2, …, en – некоторый базис векторного пространства V над полем P, а b1, b2, …, bn – произвольные векторы этого же пространства, то существует единственный линейный оператор, такой, что j(e1) = b1, j(e2) = b2, …, j(en) = bn.
Покажем, как найти образ произвольного вектора x. Разложим вектор x по базисным векторам и найдем его образ, используя свойства линейного отображения:
x = x1e1 + x2e2 + … + xnen, где xi Î Р Þ j(х) = j(x1e1 + x2e2 + … + xnen) = = j(x1e1) + j(x2e2) + … + j(xnen) = x1j(e1) + x2j(e2) + … + xnj(en) = = x1b1 + x2b2 + … + xnbn. Теорема доказана.
Пусть в векторном пространстве V задан линейный операторj,т. е. указаны образы базисных векторов j(e1), j(e2), …, j(en). Разложим эти векторы по векторамбазиса:
j(e1) = a11e1 + a21e2 + … + an1en,
j(e2) = a12e1 + a22e2 + … + an2en,
…………………………………..…..
j(en) = a1ne1 + a2ne2 + … + annen.
Используем координаты образов базисных векторов.
Определение 9.3. Матрицей линейного оператора в данном базисе называется матрица, составленная из координат образов базисных векторов, записанных в столбцы.
M(j)= 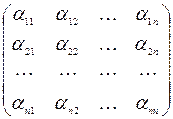 , M(j)Î Рn´n.
, M(j)Î Рn´n.
Если зафиксировать базис пространства V, то каждому линейному оператору j ставится в соответствие единственная квадратная матрица порядка: j ® M(j).
Верно и обратное: по произвольной квадратнойматрице A единственнымобразом можно задать линейный оператор j, взяв за координаты образов базисных векторов столбцы матрицы A.
Пример 9.2. 1) В пространстве V размерности 3найти матрицу оператора гомотетии.
Решение. Выбираем произвольный базис e1, e2, e3, находим образы базисных векторов j(e1) = ke1, j(e2) = ke2, j(e3) = ke3, а затем их координаты.
[j(e1)] = 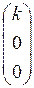 , [j(e2)] =
, [j(e2)] = 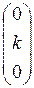 , [j(e3)] =
, [j(e3)] = 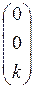 .
.
Составляем матрицу : M(j) = 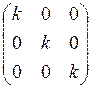 .В частности, получаем матрицы тождественного и нулевого операторов: M(e) =
.В частности, получаем матрицы тождественного и нулевого операторов: M(e) = 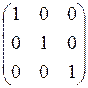 = Е, M(q) =
= Е, M(q) = 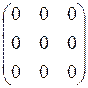 = О.
= О.
2)Найти матрицу оператора дифференцирования в пространстве R[x](£3) в базисе e1 = 1, e2 = x, e3 = x2, e4 = x3.
Решение. Найдем образы базисных векторов,их координаты и составим матрицу линейного оператора.
j(e1) = 0, j(e2) = 1, j(e3) = 2x, j(e4) = 3x2;
[j(e1)] = 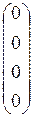 , [j(e2)] =
, [j(e2)] = 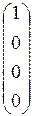 , [j(e3)] =
, [j(e3)] = 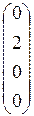 , [j(e4)] =
, [j(e4)] = 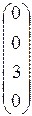 ; M(j) =
; M(j) = 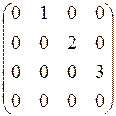 .
.
Дата добавления: 2022-04-12; просмотров: 336;










