Простейшие свойства векторных пространств

1) о – нулевой вектор (элемент), определен единственным образом в произвольном векторном пространстве над полем.

2) Для любого вектора a Î V существует единственный противоположный элемент (–a) Î V.

3) a, b Î V уравнение а + х = b разрешимо единственным образом x = b + (–a) и обозначается как x = b – a, и называется разностью.

4) операция сложения сократима: если а + b = a + c, то b = c для любых a, b, c Î V.

5) если а + b = a, то b = o.

6) если а + b = о, то а = –b и b = –a.

7) –(–а) = а.

8) 0×а = о, где 0 элемент поля P, а о – нулевой вектор пространства V.

9) k×о = о, здесь k Î P, о Î V.

10) если k×а = о, то k = 0 или а =о.

11) (–1)×а = –а.

12) (k – l)×a = k×a – l×a, где k, l Î P, а Î V.

13) k×(a – b) = k×a – k×b, где k Î P, а, b Î V.

14) (–k)×а = –k×а.

Линейная зависимость и независимость системы векторов

Для произвольного векторного пространства понятия линейной комбинации, линейной оболочки системы векторов, линейной зависимости и независимости системы векторов определяется точно так, как и для n-мерного арифметического векторного пространства. Выполняются все свойства линейной зависимости (кроме свойства, связанного со ступенчатой системой векторов).

Подпространства. Линейные многообразия

Пусть V – векторное пространство, L Ì V (L подмножество V).

Определение 8.2. Подмножество L векторного пространства V называется подпространством пространства V, если

1. " а, b Î L : а + b Î L;

2. " а Î L, k Î P: k×а Î L.

Обозначение L 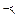V. Принято говорить, что подмножество L замкнуто относительно сложения векторов и относительно умножения их на элемент из поля P.

Пример 8.2.

1)В каждом векторном пространстве есть два подпространства, называемых несобственными: L = {0} – нулевое подпространство, L = V – подпространство, совпадающее со всем пространством .

Приведем примеры собственных подпространств.

2) Пусть V = R⁴, L = {((a₁, a₂, a₃, 0), a_i Î R} – подпространство, так как для произвольных векторов а = (a₁, a₂, a₃, 0) Î L и b = (b₁, b₂, b₃, 0) Î L и k Î P:

• а + b = (a₁ + b₁, a₂ + b₂, a₃ + b₃, 0 + 0) Î L;

• k×a = (k×a₁, k×a₂, k×a₃, 0) Î L.

3)В пространстве квадратных матриц подпространство образует подмножество диагональных матриц.

4) В пространстве направленных отрезков подпространством является множество отрезков, лежащих на прямой, проходящей через начало координат.

Теорема 8.1. Линейная оболочка L(а₁, а₂, …, а_m) системы векторов а₁, а₂, …, а_m образует подпространство пространства V.

В этом случае принято говорить, что L(а₁, а₂, …, а_m) подпространство, натянутое на векторы а₁, а₂, …, а_m, или что L(а₁, а₂, …, а_m) – подпространство, порожденное векторами а₁, а₂, …, а_m. Система векторов а₁, а₂, …, а_m называется системой образующих подпространства
L(а₁, а₂, …, а_m).