Отношение эквивалентности

Определение 2.15. Бинарное отношение на множестве А называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Отношение эквивалентности обычно обозначают символами ~ или º.

Примерами отношения эквивалентности являются отношение равенства на множестве действительных чисел, отношение параллельности на множестве прямых евклидовой плоскости, подобие треугольников на плоскости.

Определение 2.16. Пусть R – отношение эквивалентности на множестве А и а Î А. Классом эквивалентности, порожденным элементом а, называется множество a/R = [a]_R = {х Î А | (х, а) Î R}.

Совокупность всех классов эквивалентности отношения R на множестве А обозначается через А/R.

Определение 2.17.Представителем класса эквивалентности называется любой элемент этого класса.

Определение 2.18.Пусть А – непустое множество. Фактор- множеством множества А по отношению эквивалентности R называется множество A/R всех классов эквивалентности.

Определение 2.19.Разбиением непустого множества А называется совокупность его непустых подмножеств, таких что объединение всех подмножеств есть множество А, а пересечение любых двух различных подмножеств есть пустое множество.

Теорема 2.1.Пусть R – отношение эквивалентности на непустом множестве А. Тогда фактор-множество A/R является разбиением множества А.

Доказательство. Так как отношение R рефлексивно, то для любого a Î A имеем (а, а) Î R. Это значит, что каждый элемент a множества А принадлежит классу эквивалентности a/R. Итак, имеем семейство непустых классов a/R (a/R содержит по крайней мере один элемент a) и 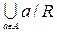= A. Осталось доказать, что пересечение любых двух различных классов пусто. Для этого достаточно показать, что классы эквивалентности, имеющие хотя бы один общий элемент, совпадают. Пусть a/R и b/R – классы эквивалентности, имеющие общий элемент c. Тогда (с, а) Î R и (c, b) Î R. В силу симметричности отношения R из (c, a) Î R следует (a, c) Î R. Пусть х – любой элемент из a/R , тогда (х, a) Î R. Имеем, (х, a) Î R и (а, с) Î R. Следовательно, в силу транзитивности отношения R (х, с) Î R. Имеем, (х, с) Î R и (с, b) Î R. Тогда (х, b) Î R, так как отношение R транзитивно. Следовательно, x Î b/R. Таким образом, a/R Í b/R. Аналогично доказывается, что b/R Í a/R. Следовательно, a/R = b/R.

Из теоремы 2.1 непосредственно вытекает следующее следствие.

Следствие.Пусть R – отношение эквивалентности на множестве А. Тогда

1) " a Î А, a Î a/R;

2) 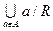= A;

3) " а, b Î А, а/R = b/R Û (а, b) Î R;

4) а/R ≠ b/R Û а/R ∩ b/R = Æ.

Пусть S – разбиение непустого множества А и R_S – бинарное отношение, определяемое следующим образом: (x, y) Î R_S тогда и только тогда, когда x и y принадлежат одному и тому же подмножеству семейства S.

Теорема 2.2. Отношение R_S,соответствующее разбиению S непустого множества А, является отношением эквивалентности на А, причем фактор-множество А/R_S совпадает с разбиением S.

Доказательство. 1. Так как S есть разбиение, то " a Î А, $ М_i Í S : a Î М_i. Следовательно, по определению отношения R_S, (а, а) Î R_S, а значит R_S – рефлексивно.

2. Пусть a, b – произвольные элементы из А такие, что (а, b) Î R_S. Тогда, по определению отношения R_S, $ М_j Í S : a, b Î М_j. Следовательно, (b, a) Î R_S. Получили, что R_S – симметрично.

3. Пусть a, b, c – произвольные элементы из А такие, что (а, b) Î R_S и (b, c) Î R_S. Следовательно, по определению отношения R_S, $ M_i , M_j Í S: a, b Î M_i и b, c Î M_j. Отсюда b Î M_i Ç M_j. Но тогда, по определению разбиения, M_i = M_j , а значит, a, c Î M_i , и, по определению отношения R_S, (a, c) Î R_S. Получили, что R_S – транзитивно.

Из п. 1 – 3 следует, что R_S – отношение эквивалентности. Фактор-множество A/R_S совпадает с разбиением S по определению отношения R_S.

Замечание 2.2. Частным случаем отношения эквивалентности ~ является отношение равенства элементов некоторого множества А, которое определяет разбиение множества на одноэлементные классы эквивалентности: " x Î A, x/~ = {x}. В этом случае классов эквивалентности оказывается столько же, сколько элементов содержится в множестве А, так как каждый элемент из А эквивалентен только самому себе.

В другом частном случае все элементы множества А эквивалентны друг другу. При этом фактор-множество А/~ состоит всего из одного класса – самого множества А.

В любом другом случае среди классов эквивалентности имеется хотя бы один класс, который содержит больше одного элемента и в то же время не совпадает с самим множеством А.

Замечание 2.3.Понятие отношения эквивалентности имеет большое значение в математике. Дело в том, что элементы, входящие в один класс эквивалентности неразличимы с точки зрения рассматриваемого отношения эквивалентности. Поэтому считают, что класс эквивалентности определяется любым своим представителем (произвольным элементом этого класса). Это позволяет вместо всех элементов множества изучать совокупность представителей каждого класса эквивалентности. Свойства, которыми обладают все элементы некоторого класса эквивалентности, изучаются на одном его представителе.

Отношения эквивалентности играют важную роль в определении математических понятий.

Функции

Определение 2.20.Бинарное отношение ƒ Í A ´ B называется функцией из множества A в множество B, еслидля любого x Î A существует единственный элемент y Î B такой, что (x, y) Î ƒ. При этом элемент y обозначается через ƒ(x) и называется значением функции ƒ для аргумента x. Функция f из A в B обозначается через ƒ: A → B или A 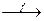B. Если (x, y) Î ƒ, то используется общепринятая запись y = ƒ(x), а также запись ƒ: x 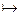y (означает, что функция ƒ ставит в соответствие элементу x элемент y).

Область определения и область значений функции, равные функции определяются так же, как и для бинарных отношений.

Аргументами функции могут являться элементы произвольной природы, в частности, кортежи длины n (x₁, x₂, …, x_n). Функцию ƒ: Aⁿ → B называют n-местной функцией из A в B. Тогда пишут y = ƒ(x₁, x₂, …, x_n) и говорят, что y есть значение функции ƒ при значении аргументов x₁, x₂, …, x_n.

Функции называются также отображениями. Пусть ƒ – функция из A в B. Если A = Domƒ и Imƒ Í B, то говорят, что ƒ есть отображение множества A в множество B. Если A = Domƒ и B = Imƒ, то говорят, что ƒ есть отображение множества A намножествоB.

Определение 2.21.Функция ƒ Í A ´ B называется инъективной, или инъекцией, если " x, y Î A, ƒ(x) = ƒ(y) Þ x = y.

Определение 2.22.Функция ƒ Í A ´ B называется сюръективной, или сюръекцией, если для каждого элемента y Î B существует хотя бы один элемент x Î A такой, что y = ƒ(x).

Заметим, что сюръективная функция ƒ Í A ´ B является отображением A на B.

Определение 2.23.Функция ƒ Í A ´ B называется биективной (биекцией) или взаимно однозначным соответствием между множествами A и B, если она одновременно инъективна и сюръективна.

Определение 2.24.Если соответствие, обратноек функции ƒ Í A ´ B, является функциональным и полностью определенным, то оно называется функцией, обратной к ƒ и обозначается ƒ^–1.

Так как в обратном соответствии образы и прообразы меняются местами, то для существования функции, обратной к функции f Í A ´ B,необходимо и достаточно, чтобы Imf = B и каждый элемент y Î Imf имел единственный прообраз.

Утверждение 2.3.Для функции ƒ: A → B существует обратная к ней функция ƒ^–1: B → A тогда и только тогда, когда ƒ – биекция.

Определение 2.25.Пусть даны функции ƒ: A → B и g: B → C. Функция h: A → C называется композицией (суперпозицией) функций f и g, если " x Î A, h(x) = g(f(x)).

Композиция функций f и g обозначается через g _° f, при этом знак _° часто опускается.