Метод математической индукции

Метод математической индукции используется для доказательства утверждений, в формулировке которых участвует натуральный параметр n. Метод математической индукции – метод доказательства математических утверждений, основанный на принципе математической индукции. Сформулируем этот принцип: утверждение A(n), зависящее от натурального параметра n, считается доказанным, если доказано A(1) и для каждого натурального числа k из предположения, что верно A(k) выведено, что верно A(k + 1).

Доказательство методом математической индукции состоит из трех этапов.

База индукции: проверяем, что A(n) верно при n = 1.

Предположение индукции: предполагаем, что A(k) истинно.

Шаг индукции: доказываем, используя предположение, что истинно A(k + 1).

Замечание 1.6.Если требуется доказатьутверждение А(n), где n Î N₀, то база индукции начинается с n = 0.

Замечание 1.7.Доказательство методом математической индукции можно начинать не с 1, а с любого натурального m. В этом случае утверждение считается истинным при n ³ m.

Замечание 1.8.С помощьюпринципа математической индукции можно давать индукционные определения. При этом для определения понятия А(n) (n ÎN), во-первых, задается значение А(1); во-вторых, для любого натурального числа k задается правило получения значения А(k + 1) по числу k и значению А(k).

Пример 1.11. Доказать равенство: 1 + 2 + … + n = .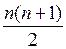

Доказательство. Пусть А(n) = 1 + 2 + … + n.

База индукции: для n = 1 имеем верное равенство 1 = .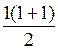

Предположение индукции: пусть для n = k имеем верное равенство: 1 + 2 + … + k = .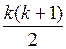

Шаг индукции: докажем, что при n = k + 1 будет верно равенство: 1 + 2 + … + k + (k + 1) = 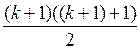. Преобразуем левую часть этого равенства 1 + 2 + … + k + (k + 1) = А(k) + (k + 1) = 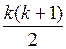+ (k + 1) = = 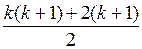= = 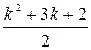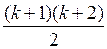. Получили, что из истинности равенства при n = k (k – произвольное натуральное число) следует его истинность при n = k + 1.

По принципу математической индукции утверждение A(n) верно при любом натуральном n.

Комплексные числа

Понятие числа является одним из основных завоеваний человеческой культуры. Сначала появились натуральные числа N = {1, 2, 3, …, n, …} затем целые Z = {…, –2, –1, 0, 1, 2, …}, рациональные Q = { 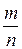| m Î Z, n Î N} (для того чтобы всякое уравнение вида а×х = b, где а ≠ 0 имело решение); потом появились иррациональные числа это было связано с решением квадратных уравнений, например х² = 2, на множестве рациональных чисел это уравнение не имеет решения. Иррациональные числа – это бесконечные непериодические десятичные дроби, например p, е, 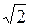, , 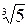…. Рациональные числа можно представить конечными или бесконечными периодическими десятичными дробями, например 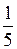= 0,2; 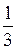= 0,(3). Рациональные и иррациональные числа образуют множество R действительных чисел. На этом множестве уравнение х² = 2 уже имеет два корня х₁ = 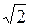и х₂ = – 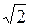. Но действительных чисел оказалось недостаточно для того, чтобы, например решить квадратное уравнение вида х² + 1 = 0 (т. к. на множестве действительных чисел нет такого числа, квадрат которого отрицателен). Поэтому ввели комплексные числа C. Впервые упоминание о комплексных числах появилось в работах итальянского ученого Кардано[5] в 1545 г., когда он пришел к выражению 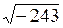, решая кубическое уравнение х³ –12х + 16 = 0. Термин «комплексное число» ввел немецкий математики Гаусс[6] в 1831 г. Первоначально комплексные числа называли мнимыми. И только когда датчанин Вессель[7](1799 г.) (независимо от него француз Арган[8] (1806 г.) и немец Гаусс (1832 г.)) дал геометрическое истолкование комплексного числа, они получили признание и нашли широкое применение.

Уравнение вида х² + 1 = 0 приводит к понятию мнимой единицы. Решая это уравнение, получаем х² = –1 или х = 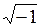; 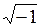назвали мнимой единицей и обозначили i = 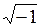или i² = –1.

Определение 1.17.Комплексным числом называется выражение вида a + b×i, где a, b Î R, i = 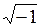– мнимая единица.

Комплексное число z = a + b×i состоит из двух частей: число а = Rez– называется действительной частью z, b = Imz – мнимой частью комплексного числа z.

Используют следующие термины: если b = 0, то a + 0×i = а – действительное число (точнее отождествляют с действительным числом), в частности 0 + 0×i = 0; если а = 0, то числа вида b×i (b ≠ 0) называют чисто мнимым. Множество всех комплексных чисел обозначают C = {a + b×i | a, b Î R, i = 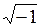} при этом R Ì C.

Определение 1.18.Комплексное число, записанное в виде z = a + b×i, называется алгебраической формой записи комплексного числа.

Определение 1.18. Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части равны, т. е. a + b×i = с + d×i Û a + с и b = d.

Определение 1.19. Комплексные числа вида a + b×i и a – b×i называются сопряженными.

Определение 1.20. Комплексные числа вида a + b×i и –a – b×i называются противоположными.