Подмножества. Диаграммы Эйлера – Венна
Определение 1.4.Множество B называется подмножеством множества A, если каждый элемент множества B принадлежит множеству A.
Пример 1.2.Пусть А = {1, 2, 3, 4, 5, 6, 7}, а B = {2, 3, 5, 7}. Множество В является подмножеством множества А, поскольку каждый элемент множества В принадлежит множеству А.
Если множество B является подмножеством множества A, то говорят также, что B содержится в A или B включено в A, при этом пишут В Í А или А Ê В. Символ Í называется знаком включения (точнее, нестрого включения).
Согласно данному определению 1.4 подмножества, каждое множество является подмножеством самого себя, то есть (" A) А Í А. Кроме того, считается, что пустое множество есть подмножество любого множества A: (" A) Æ Í А.
Различают два вида подмножеств множества А.
Определение 1.5.Пустое множество Æ и множество А называются несобственными подмножествами множества А.
Определение 1.6.Любые подмножества множества А, отличные от А и Æ, называются собственными подмножествами множества А.
Определение 1.7. Множества A и B, состоящие из одних и тех же элементов, называются равными. При этом пишут А = В, в противном случае А ≠ В.
Справедливо следующее утверждение, которое также можно рассматривать в качестве определения равных множеств.
Утверждение 1.1. А = В Û А Í B и В Í А.
Замечание 1.3.Из утверждения 1.1 вытекает способ доказательства равенства двух множеств: если доказать, что каждый элемент из множества A является элементом множества B и каждый элемент из множества B является элементом множества A, то делают вывод, что А = В.
Говорят, что множество B строго включено в множество A или, по-другому, А строго включает B, если В Í А и В ¹ А. В этом случае пишут B Ì A. Символ Ì называется знаком строгого включения.
Пример 1.3.Имеют место следующие строгие включения числовых множеств: N Ì N0 Ì Z Ì Q Ì R Ì C и IÌ R Ì C.
Определение 1.8.Совокупность всех подмножеств множества A называется его булеаном (или множеством-степенью), и обозначается через P(A) (или 2A).
Пример 1.4. Если A = {a, b, c}, то булеан множества А это множество P(A) = {Æ, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}}.
Для наглядного изображения множеств и их свойств используют так называемые диаграммы Эйлера[2] – Венна[3]. Множество отождествляется с множеством точек на плоскости, лежащих внутри некоторых замкнутых кривых, например окружностей (так называемые круги Эйлера). В частности, универсальное множество U изображается множеством точек некоторого прямоугольника или всей плоскости (рис. 1.1).
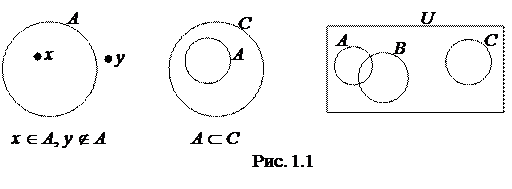
Дата добавления: 2022-04-12; просмотров: 165;










