Ряды с неотрицательными членами.
Если известно, что все члены ряда 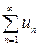 имеют, начиная с некоторого номера, постоянный знак, то исследовать его сходимость проще, чем в общем случае. Это связано с простым критерием сходимости для таких рядов. Для простоты предположим, что все
имеют, начиная с некоторого номера, постоянный знак, то исследовать его сходимость проще, чем в общем случае. Это связано с простым критерием сходимости для таких рядов. Для простоты предположим, что все 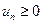 .
.
Отсюда вытекают три простых свойства рядов с неотрицательными членами.
· Последовательность частичных сумм неотрицательна, т.е. 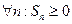 .
.
· Последовательность частичных сумм монотонна, т.е. 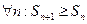 .
.
· Для того чтобы последовательность частичных сумм сходилась необходимо и достаточно, чтобы она была ограничена:
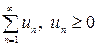 сходится
сходится 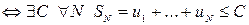 .
.
Используя последний факт, легко доказать следующие признаки сходимости числовых рядов с неотрицательными членами.
Признаки сравнения
Теорема (первый признак сравнения). Пусть 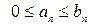 для всех
для всех 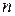 . 1. Если ряд
. 1. Если ряд 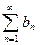 сходится, то сходится и ряд
сходится, то сходится и ряд 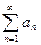 .
.
2. Если ряд 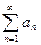 расходится, то расходится и ряд
расходится, то расходится и ряд 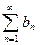 .
.
Доказательство. Если 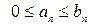 для всех
для всех 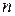 , то очевидны неравенства
, то очевидны неравенства 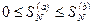 .
.
1. По условию, ряд 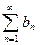 сходится. Значит, по приведенному выше критерию
сходится. Значит, по приведенному выше критерию 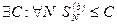 . Но тогда и
. Но тогда и 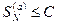 , значит, ряд
, значит, ряд 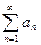 тоже сходится.
тоже сходится.
2. Пусть ряд 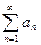 расходится. Тогда если бы ряд
расходится. Тогда если бы ряд 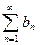 сходился, то из уже доказанного утверждения должен был бы сходиться и ряд
сходился, то из уже доказанного утверждения должен был бы сходиться и ряд 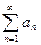 , что противоречит условию. Следовательно, расходится и ряд
, что противоречит условию. Следовательно, расходится и ряд 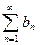 .
.
Пример.Исследовать сходимость рядов
1) 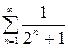 ; 1а)
; 1а) 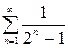 ; 2)
; 2) 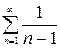 ; 2а)
; 2а) 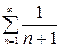 .
.
Решение. 1) Для сравнения выберем ряд 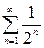 , сходимость которого доказана. Так как имеет место очевидное неравенство
, сходимость которого доказана. Так как имеет место очевидное неравенство 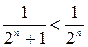 , то данный ряд сходится.
, то данный ряд сходится.
1а) Выберем для сравнения тот же сходящийся ряд 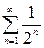 . Но неравенство
. Но неравенство 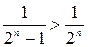 не позволяет сделать вывод о сходимости данного ряда – первая теорема сравнения не сработала.
не позволяет сделать вывод о сходимости данного ряда – первая теорема сравнения не сработала.
2) Для сравнения выберем гармонический ряд 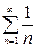 , расходимость которого установлена. В силу неравенства
, расходимость которого установлена. В силу неравенства 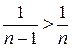 данный ряд расходится.
данный ряд расходится.
2а) Выберем для сравнения тот же расходящийся ряд 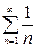 . Неравенство
. Неравенство 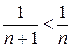 не позволяет сделать вывод о расходимости данного ряда – опять первая теорема сравнения не сработала.
не позволяет сделать вывод о расходимости данного ряда – опять первая теорема сравнения не сработала.
Примечание. Из утверждения 1 следует, что теорема справедлива и в случае, когда неравенство 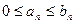 выполняется, начиная с некоторого номера
выполняется, начиная с некоторого номера 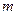 .
.
Следствие 1. Пусть 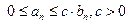 для всех
для всех 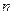 и пусть ряд
и пусть ряд 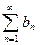 сходится. Тогда сходится и ряд
сходится. Тогда сходится и ряд 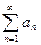 .
.
Если же 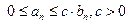 для всех
для всех 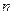 и ряд
и ряд 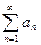 расходится, то расходится и ряд
расходится, то расходится и ряд 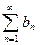 .
.
Следствие 2. Пусть 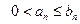 для всех
для всех 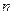 и пусть существует конечный предел
и пусть существует конечный предел 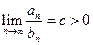 , тогда ряды
, тогда ряды 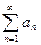 и
и 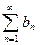 ведут себя одинаково – сходятся или расходятся одновременно (т.е. не может быть так, что один из них сходится, а другой расходится).
ведут себя одинаково – сходятся или расходятся одновременно (т.е. не может быть так, что один из них сходится, а другой расходится).
Доказательство. 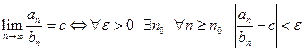 . Выберем
. Выберем 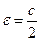 . Тогда
. Тогда 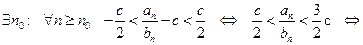 (т.к.
(т.к. 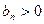 )
) 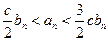 при
при 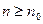 .
.
Если ряд 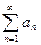 сходится, то сходится и ряд
сходится, то сходится и ряд 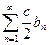 (по теореме). Но из следствия 1 получим, что и ряд
(по теореме). Но из следствия 1 получим, что и ряд 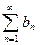 сходится.
сходится.
Если ряд 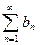 сходится, то сходится и ряд
сходится, то сходится и ряд 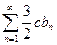 , следовательно, сходится ряд
, следовательно, сходится ряд 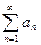
Теорема (второй признак сравнения). Пусть 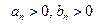 и
и 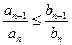 для всех
для всех 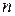 .
.
1. Если ряд 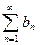 сходится, то сходится и ряд
сходится, то сходится и ряд 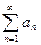 .
.
2. Если ряд 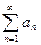 расходится, то расходится и ряд
расходится, то расходится и ряд 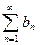 .
.
Пример. Исследовать сходимость рядов
1) 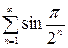 ; 2)
; 2) 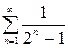 ; 3)
; 3) 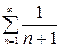 .
.
Решение. 1) Для сравнения выберем сходящийся ряд 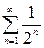 . Так как (первый замечательный предел)
. Так как (первый замечательный предел) 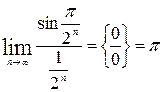 , то оба ряда ведут себя одинаково – данный ряд сходится.
, то оба ряда ведут себя одинаково – данный ряд сходится.
2) Опять для сравнения выберем сходящийся ряд 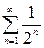 . Так как
. Так как 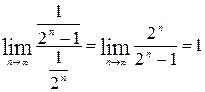 , то оба ряда ведут себя одинаково – данный ряд сходится.
, то оба ряда ведут себя одинаково – данный ряд сходится.
3) Для сравнения выберем расходящийся гармонический ряд 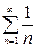 . Так как
. Так как 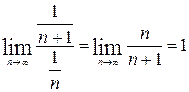 , то оба ряда ведут себя одинаково – данный ряд расходится.
, то оба ряда ведут себя одинаково – данный ряд расходится.
Признак Даламбера
Теорема (признак сходимости Даламбера). Пусть задан ряд с положительными членами 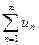 и при всех n:
и при всех n: 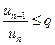 , где
, где 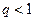 . Тогда ряд
. Тогда ряд 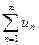 сходится. Если же при всех n для этого ряда
сходится. Если же при всех n для этого ряда 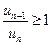 , то ряд расходится.
, то ряд расходится.
Доказательство. Пусть выполнено условие 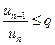 ,
, 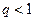 . Рассмотрим вспомогательный ряд
. Рассмотрим вспомогательный ряд 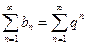 , сходящийся при
, сходящийся при 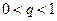 . Тогда по второй теореме сравнения ряд
. Тогда по второй теореме сравнения ряд 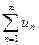 сходится, т.к.
сходится, т.к. 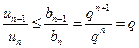 . Если же выполнено условие
. Если же выполнено условие 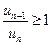 , то, взяв вспомогательный расходящийся ряд
, то, взяв вспомогательный расходящийся ряд 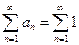 , по второй теореме сравнения получаем
, по второй теореме сравнения получаем 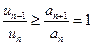 , значит, ряд
, значит, ряд 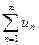 расходится.
расходится.
В предельной форме этот признак выглядит так:
Теорема. Если существует 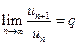 , то при
, то при 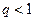 ряд
ряд 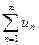 сходится, а при
сходится, а при 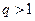 расходится. При
расходится. При 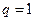 признак неприменим.
признак неприменим.
Доказательство. Пусть 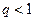 . Выбираем
. Выбираем 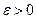 так, чтобы и
так, чтобы и 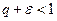 . Согласно определению предела последовательности найдется такой номер
. Согласно определению предела последовательности найдется такой номер 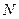 , что для всех
, что для всех 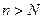 выполняется неравенство
выполняется неравенство 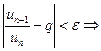
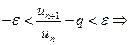
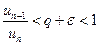 . По предыдущей теореме ряд сходится.
. По предыдущей теореме ряд сходится.
Если же 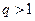 , то выберем
, то выберем 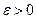 так, чтобы
так, чтобы 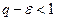 . Тогда снова найдется такой номер
. Тогда снова найдется такой номер 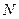 , что для всех
, что для всех 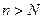 выполняется неравенство
выполняется неравенство 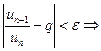
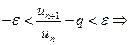
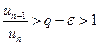 и ряд расходится.
и ряд расходится.
Пример.Исследовать сходимость рядов
1) 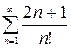 ; 2)
; 2) 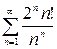 3)
3) 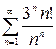 4)
4) 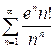 .
.
Решение. 1) Воспользуемся признаком Даламбера в предельной форме. Выпишем 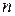 -ый и
-ый и 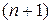 –й члены ряда и составим отношение
–й члены ряда и составим отношение
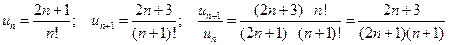 .
.
Переходя к пределу при 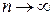 , получаем
, получаем
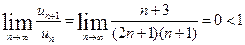 .
.
В силу признака Даламбера ряд сходится.
2) Здесь 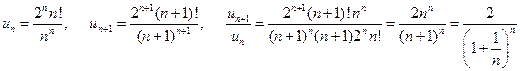 .
.
Перейдем к пределу при 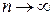 . Вспоминая, что
. Вспоминая, что 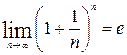 (второй замечательный предел), получаем
(второй замечательный предел), получаем 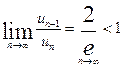 – данный ряд сходится.
– данный ряд сходится.
3) Здесь 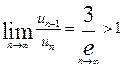 – данный ряд расходится.
– данный ряд расходится.
4) Здесь 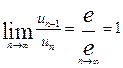 , т.е. признак Даламбера в предельной форме не решает вопроса о поведении ряда. Более точная форма признака Даламбера (без перехода к пределу) позволяет установить расходимость данного ряда. Действительно, в отношении
, т.е. признак Даламбера в предельной форме не решает вопроса о поведении ряда. Более точная форма признака Даламбера (без перехода к пределу) позволяет установить расходимость данного ряда. Действительно, в отношении 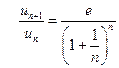 знаменатель с ростом
знаменатель с ростом 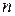 монотонно возрастает, оставаясь меньше числа
монотонно возрастает, оставаясь меньше числа 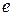 . Значит, отношение
. Значит, отношение 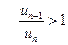 , а это означает расходимость данного ряда.
, а это означает расходимость данного ряда.
Дата добавления: 2020-05-20; просмотров: 212;










