Простейшие аппроксимации второй производной.

Из представления

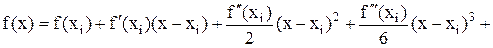
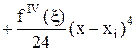
имеем

,

,

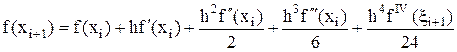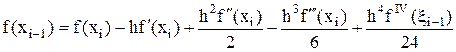откуда почленным сложением получаем

.

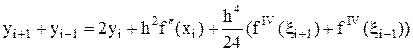Выражая из последнего равенства f"(x_i), приходим к формуле симметричной аппроксимации f"(x_i) с остаточным членом:

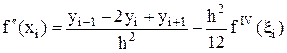. (20)

Остаточный член этой формулы 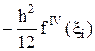с некоторым ξ_i Î (x_i–1, x_i+1) характеризует приближенное равенство

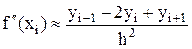, (21)

как аппроксимацию второй производной в точке x_i второго порядка точности, т. е. с погрешностью O(h²).

То же отношение 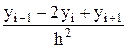, используемое в качестве несимметричной аппроксимации второй производной функции f(x), т. е. для вычисления приближенных значений f"(x_i–1) и f"(x_i+1), дает лишь первый порядок точности. Действительно, по формуле Тейлора для второй производной имеем

f"(x) = f"(x_i) + f'''(ξ)(x – x_i).

Подставляя сюда вместо f"(x_i) правую часть равенства (20), получаем

.

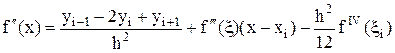Из этого равенства при x = x_i+1 и x = x_i–1 следуют частные формулы несимметричной аппроксимации второй производной с остаточными членами:

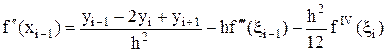и

.

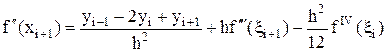С помощью формулы Тейлора можно вывести остаточные члены и других простейших аппроксимаций производных.

Более общий подход для получения выражений остаточных членов интерполяционных формул численного дифференцирования состоит в дифференцировании остаточного члена интерполяционной формулы Лагранжа. Имеем,

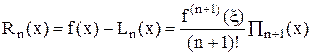, (22)

где L_n(x) — интерполяционный многочлен Лагранжа, построенный для n + 1 раз дифференцируемой функции f(x) по n + 1 узлу x₀, x₁, …, x_n (неважно, в какой форме), ξ — некоторая точка из интервала (х₀, x_n), а П_n+1(x) = (x – х₀)´
´(x – x₁)...(x – x_n). Из (22) следует

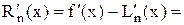
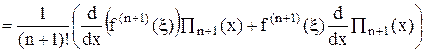. (23)

Если величина 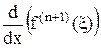ограничена, то при подстановке в последнее выражение узловых значений x = x_i (i = 0, 1, …, n) за счет П_n+1(x_i) = 0 получим простую формулу остаточного члена аппроксимаций f¢(x_i) » L¢(x_i) первой производной в узлах интерполяции:

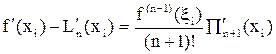, ξ_i Î (x₀, x_n). (24)

В случае равноотстоящих узлов x_i = x₀ + ih, который здесь, в основном, и рассматривается,

,

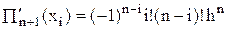вследствие чего равенство (24) трансформируется в формулу

. (25)

Из нее отчетливо видно, что при аппроксимации первой производной в точках x_j значениями 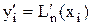, получаемыми дифференцированием интерполяционного многочлена n-й степени, остаточный член имеет n-й порядок относительно шага аппроксимации h.

Воспользуемся формулой (25), чтобы выписать остаточные члены несимметричных аппроксимаций первой производной (8) и (10). При n = 2, i = 0 и i = 2 из (25) следует

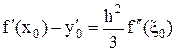
и

.

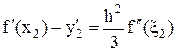Ставя эти формулы в один ряд с формулой (18), имеем:

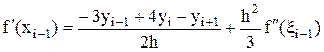, (26)

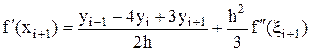. (27)

Заметим, что формулы несимметричной аппроксимации f'(x_i–1) (26) и f'(x_i+1) (27) второго порядка точности имеют в остаточном члене вдвое больший коэффициент, чем формула симметричной аппроксимации (18).

Для оценивания погрешности численного дифференцирования при значениях аргумента, не совпадающих с узловыми, и для получения остаточных членов приближенных формул 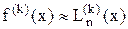при k > 1 формула (23) малопригодна. На основе интерполяционной формулы Ньютона для неравных промежутков и связей между разделенными разностями и производными выводятся следующие формулы остаточных членов:

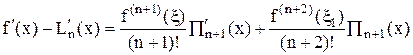, (28)

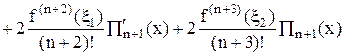, (29)

и вообще, для k Î {0, 1, …, n}

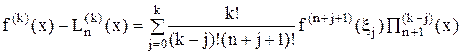. (30)

Имеются и другие, отличные от (28)-(30) представления остаточных членов и оценок погрешностей интерполяционных формул численного дифференцирования.

Так как остаточные члены формул численного дифференцирования выражаются через производные более высоких порядков, чем искомые производные, то «в чистом виде» подобные выражения остаточных членов малопригодны для практического оценивания погрешностей. Однако не стоит считать их совсем бесполезными. Во-первых, они важны для качественного сравнения (например, по порядку) различных аппроксимаций производных. Во-вторых, их можно применить для оценивания точности результатов численного дифференцирования, пользуясь простейшими связями между производными и конечными (или разделенными) разностями, например, составляя таблицы конечных разностей до требуемого в оценке порядка и принимая за max|f⁽ⁿ⁺¹⁾(x)| величину max(|Δⁿ⁺¹y_i|)/hⁿ⁺¹ в соответствующей области таблицы. В третьих, выполнение условий, при которых справедливы те или иные формулы аппроксимации производных на равномерной сетке, позволяет при вычислении значений производных применять принцип Рунге двойного счета с разными шагами подобно тому, как это делается при вычислении интегралов.