ФОРМУЛы ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ

Численное дифференцирование, т. е. нахождение значений производных заданной функции у = f(x) в заданных точках x, в отличие от, например, численного интегрирования, можно считать не столь актуальной задачей в связи с отсутствием принципиальных трудностей с аналитическим нахождением производных. Однако имеется ряд моментов, не позволяющих обходить эту задачу стороной. Это и типичное для прикладных задач незнание аналитического вида f(x), и возможное сильное усложнение функции при ее аналитическом дифференцировании (что затрудняет нахождение ее значений с высокой точностью), и желательность получения значений производных с помощью однотипных вычислительных процессов без привлечения аналитических выкладок. Главным же для дальнейшего является потребность в простых формулах, с помощью которых производные в заданных точках можно аппроксимировать несколькими значениями функции (быть может неизвестной) в этих и близких к ним точках.

Источником формул численного дифференцирования, как и большинства квадратурных формул, является полиномиальная интерполяция.

Зная в точках x_i = x₀ + ih (i = 0, 1, …, n) при некотором h > 0 значения у_i = f(x_i) данной функции y = f(x), можно найти конечные разности Δ^ky_i и записать для нее, например, первый интерполяционный многочлен Ньютона P_n(x).

Дифференцируя приближенное равенство f(x) » P_n(x), будем строить формулы приближенного дифференцирования разной точности в зависимости от степени n используемого интерполяционного многочлена. Через вспомогательную переменную 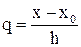приближенное представление функции f(x) по первой формуле Ньютона выглядит наиболее просто:

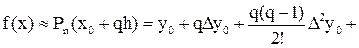
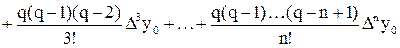. (1)

Отсюда получаем конечноразностную формулу численного дифференцирования

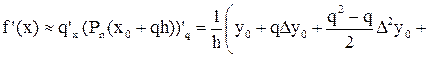
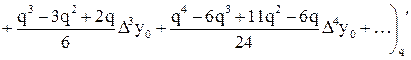, т. е.

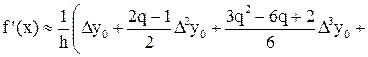
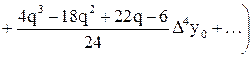. (2)

При использовании последнего равенства для приближенного вычисления производной функции f(x) в заданной точке x из некоторой окрестности точки x₀ следует найти соответствующее значение 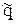переменной 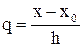и подставить его в формулу (2). Максимальный порядок конечных разностей в этой формуле при желании получить производную с наибольшей точностью определяется в конкретной ситуации в соответствии с приведенными ранее соображениями о выборе подходящей степени интерполяционного многочлена.

Аналогично можно вывести ряд других формул численного дифференцирования на основе различных интерполяционных формул, более эффективно «работающих» вблизи других узловых точек и в общем случае не обязательно равноотстоящих. Вернемся к приближенной формуле (2). Рассмотрим несколько ее частных случаев, фиксируя степень n лежащего в ее основе интерполяционного многочлена (1), равной 1, 2, 3. Этим значениям n отвечают соответственно одно, два, три первых слагаемых в формуле (2). Таким образом, имеем:

на основе линейной интерполяции

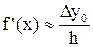для x Î (x₀ – d; x₁ + d), (3)

на основе квадратичной интерполяции

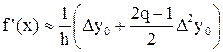для x Î (x₀ – d; x₂ + d), (4)

на основе кубической интерполяции

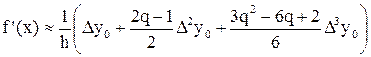(5)

для x Î (x₀ – d; x₃ + d),

и т. д. (при некоторых δ > 0, определяющих промежуток экстраполяции приемлемого качества соответствующей интерполяционной формулой).

Для дальнейшего особый интерес представляют частные случаи формул (3)-(5), связывающие приближенное значение производной функции f(x) в узлах x₀, x₁, … с узловыми значениями самой функции. Учитывая, что точкам x₀, x₁, x₂, x₃ соответствуют значения q = 0, 1, 2, 3, и раскрывая конечные разности через значения y_i (i = 0, 1, 2, 3), имеем:

при n = 1 из (3)

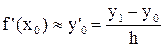, (6)

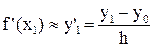, (7)

при n = 2 из (4)

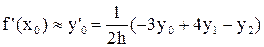, (8)

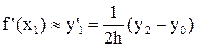, (9)

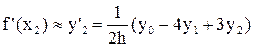, (10)

при n = 3 из (5)

,

,

,

.

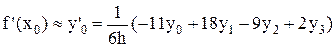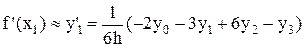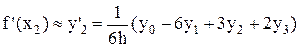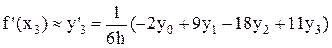В случае необходимости этот ряд формул можно продолжить с помощью общей формулы (2) или посмотреть в других источниках.

Повторное дифференцирование приближенного равенства (1), т. е. взятие производной по x от правой части формулы (2) с учетом 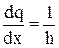, приводит к конечноразностной формуле вычисления второй производной

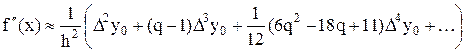(11)

из которой таким же образом следует приближенная формула для третьей производной

,

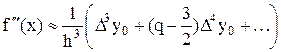и т. д.

Наиболее важной в приложениях является простейшая аппроксимация второй производной с помощью постоянной 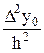на промежутке (x₀ – δ, x₂+d), получающаяся из (11) фиксированием только одного слагаемого (случай n = 2). В частности, в точке x₁ имеем приближенное равенство

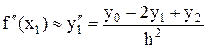, (12)

которое вместе с формулами (6)-(10) широко используется при построении конечноразностных методов решения краевых задач для обыкновенных дифференциальных уравнений второго порядка и для уравнений в частных производных.