Оценка точности регрессионных моделей.

Наиболее просто оценка точности результатов моделирования производится для моделей типа «черного ящика», или моделей типа «вход-выход», если модель системы удается представить системой линейных регрессионных уравнений [11]. Рассмотрим модель, состоящую из m линейных уравнений с n неизвестными 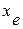. Эти уравнения разбиваются на два полных и взаимно исключающих класса М₁ и М₂. Соответственно на два класса N₁ и N₂ разделяются переменные. Для оценки точности результатов моделирования необходимо найти максимум 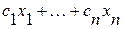при заданных ограничениях:

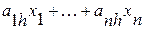
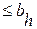для всех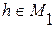

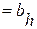для всех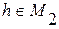

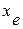неотрицательны для всех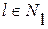

произвольны для всех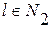

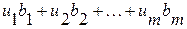Соответствующая двойственная модель состоит из n линейных уравнений с m неизвестными U_h. Необходимо минимизировать при заданных ограничениях:

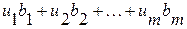
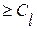для всех 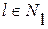(4.3.1а)

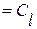для всех 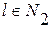(4.3.1.б)

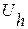неотрицательны для всех 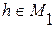(4.3.1.в)

произвольны для всех 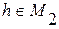(4.3.1.с)

Пусть 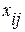(i=1, 2, …, k; j=1, 2, …, p) есть множество k наблюдений для каждой из p независимых переменных, 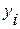(i=1, 2, …, k) есть множество наблюдений величины зависимых переменных. Мы хотим найти регрессионные коэффициенты 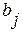, минимизирующие выражение:

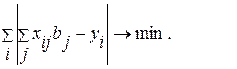(4.3.2.)

Задачу (4.3.2) можно свести к следующей:

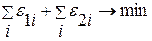при ограничениях: 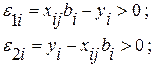(4.3.3)

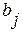- произвольны по знаку ; .

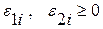Здесь 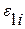и 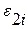интерпретируются как отклонения по вертикали выше и ниже линии, аппроксимирующей i-ую серию наблюдений. Согласно (4.3.3) знак 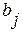произволен, что становится несущественным, если в контексте регрессионной проблемы мы хотим ограничиться только неотрицательными 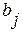; либо наложить на 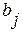дополнительные, более сложные линейные ограничения.

По мере увеличения числа наблюдений k за системой, задачу (4.3.1) с ограничениями (4.3.3) все труднее решить численно. Можно, однако, преобразовать (4.3.2) и (4.3.3) к более удобной для решения двойственной задаче, решая которую мы попутно получим оптимальные значения 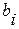. Для сохранения общности в нашем рассмотрении положим, что 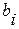распадается на два класса – М₁ и М₂ в соответствии с (4.3.1.с) и (4.3.1.d). Тогда двойственная связь, описанная выше, означает, что мы можем найти решение (4.3.2.) с ограничениями (4.3.3.) только в том случае, если удастся максимизировать:

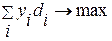(4.3.4)

при ограничениях: 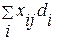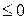для всех 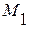(4.3.5а)

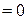для всех 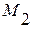(4.3.5б)

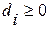i=1, 2, …, k (4.3.6.в)

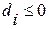i=1, 2, …, k (4.3.6.г)

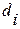произвольны по знаку (4.3.6.д)

Модель (4.3.5) с ограничениями (4.3.6) представляет собой еще более сложную проблему по сравнению с (4.3.2) и (4.3.3), поскольку насчитывает p+2k уравнений. Чтобы свести ее к модели с p уравнениями и k связанными переменными, положим:

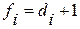i=1, 2, …, k, (4.3.7)

тогда (6.2.5) и (6.2.6) эквивалентны задаче:

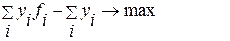(4.3.8)

при ограничениях: 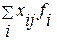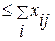для всех 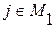(4.3.9.а)

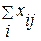для всех 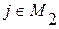(4.3.9.в)

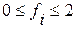i=1, 2, …, k. (4.3.9.с)

Теперь модель оказывается состоящей из p линейных уравнений (4.3.9.а) и (4.3.9.в) со связанными неотрицательными переменными (4.3.9.с). Существующая техника решения задач линейного программирования [14] позволяет получить оптимальный «базисный» набор переменных. Обозначим эти оптимальные базисные переменные 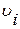(i=1, 2, …, p). За 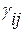обозначим коэффициент при 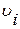, а за 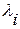- соответствующие коэффициенты в (4.3.8). Тогда регрессионные коэффициенты удовлетворяют уравнениям:

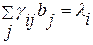i=1, 2, ..., p (4.3.10)

Оптимальное значение (4.3.10) есть минимизированная сумма абсолютных отклонений. Если наложить дополнительные ограничения на 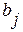, то это приведет к появлению новых переменных в (4.3.9); число уравнений при этом остается неизменным, также как и размерность (4.3.10).

Теперь рассмотрим регрессионную задачу, которая по сравнению с моделью, рассмотренной выше, содержит на одно уравнение выше, но в ней отсутствует ограничение на «связанные» переменные. Используя критерий Чебышева, ищем 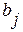из условия:

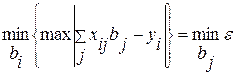. (4.3.11)

Затем преобразуем (4.3.11) в задачу линейного программирования:

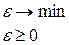(4.3.12)

при ограничениях: 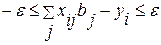, i=1, 2, …, k. (4.3.13)

В (4.3.12) и (4.3.13) 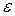есть минимизированное значение максимального абсолютного отклонения. Полагаем 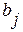разбитыми на два класса в соответствии с (4.3.1.с) и (4.3.1.d). Чтобы использовать теорему о двойственности, запишем (4.3.2) и (4.3.3) в более общем виде:

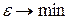(4.3.14)

при ограничениях:

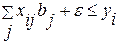i=1, 2, …, k (4.3.15а)

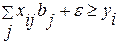i=1, 2, …, k (4.3.15b)

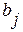не отрицательны для всех 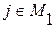, (4.3.15с)

произвольны по знаку для всех 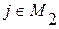, (4.3.15d)

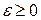. (4.3.15е)

Двойственность тогда формулируется следующим образом:

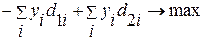(4.3.16)

при ограничениях: 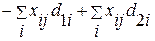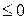для всех 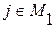(4.3.17а)

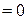для всех 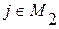(4.3.17b)

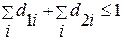; (4.3.17с)

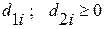(4.3.17d)

Модель (4.3.16) с ограничениями (4.3.17) представляет собой задачу линейного программирования для p+1 уравнения, которая решается стандартными методами. Если 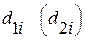положительны для оптимального решения (4.3.16), то максимальное отклонение имеет место для i-го наблюдения, т.е. для i-го уравнения в (4.3.15а), (4.3.15b), и эта i-ая точка лежит выше (ниже) аппроксимирующей прямой. Коэффициенты регрессии получим из оптимального решения (4.3.16), используя следующие соотношения /20/: 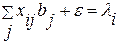i=1, 2, …, p+1

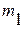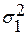Для оценки качества прогноза сначала определяются параметры и для выборки 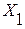. Для выборки 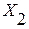(выборки модельных значений) параметры 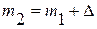; 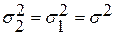заданы; 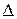- некоторый параметр, характеризующий допустимый для рассматриваемого метода разброс модельных точек относительно реальных, он может быть равен 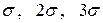и т.д. но не более .

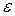Вычисляем для совокупности модельных значений последовательно минимальное и максимальное значение суммы 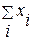с тем, чтобы по этим значениям выбрать такие А и В, для которых выполнялось бы неравенство:

,

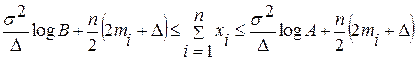т.е. определяем: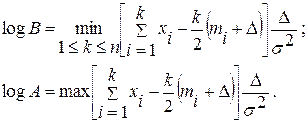

Затем вычисляем А и В, после чего находим вероятность 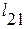того, что прогнозное значение принимается за реальное, что и будет характеризовать ошибку прогноза, из системы уравнений:

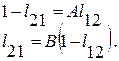
Учитывая правильность нормального распределения для выборки 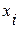, можно построить доверительный интервал для :

.

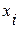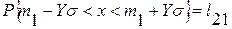Зная величину Р по таблицам нормального распределения, находим величину 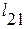, поскольку ,

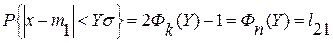где .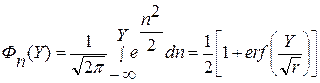

Прогностические возможности модели «вход-выход» ограничены в связи со структурными различиями между такой моделью и самим моделируемым объектом. Следует учитывать также эффект «накопления ошибок», возникающий при наличии последовательности блоков модели, когда выход из некоторого блока служит входом для следующего блока.

Если мы пытаемся описать реальный процесс, происходящий в системе, аналитической функцией f(x), то теория ошибок дает возможность оценить погрешность расчета с помощью производной этой функции. Для линеаризованного приближения 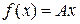погрешность определения функций будет равна: 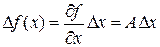, где 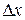- погрешность определения аргумента.

В случае функции нескольких переменных 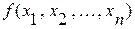погрешность равна: .

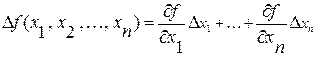Если используется функция более сложного вида, например 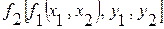, то погрешность определяется как

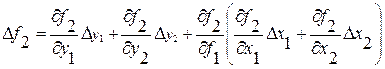, и т. д.

Ошибки в моделях такого рода имеют свойство накапливаться, отсюда возникает необходимость увеличения точности расчетов при построении регрессионных моделей систем.

Контрольные вопросы

1. Почему при моделировании систем очень важным является изучение Марковских процессов?

2. Что такое стохастический процесс?

3. Как описывается пространство состояний системы, в которой происходит стохастический процесс?

4. Что представляет собой вектор состояний эволюционирующей системы в любой момент времени?

5. Дайте определение Марковской цепи.

6. Какая Марковская цепь называется однородной?

7. Как составляется и для чего служит стохастическая матрица Марковской цепи?

8. Как строится размеченный граф состояний системы, если известна стохастическая матрица?

9. Как математически записывается переход на один шаг вперед в однородной Марковской цепи?

10. Что такое предельный вектор Марковской цепи?

11. По какой причине прогноз погоды часто оказывается неверным?

12. В чем заключаются недостатки статистических методов прогнозирования по сравнению с причинно-следственными методами?

13. Какому закону статистики обычно подчиняются исходные данные для анализа временного ряда?

14. Какой степени полином чаще всего используется для сглаживания временных рядов?

15. В чем сущность метода скользящего среднего?

16. Какой метод используется для определения параметров прямой, аппроксимирующей временной ряд?

17. Сформулируйте теорему Байеса.

18. Для каких целей служат регрессионные модели систем?

19. Относится ли построение регрессионных моделей к статистическим или причинно-следственным методам моделирования?

20. Для какого типа моделей наиболее просто производится оценка точности результатов оптимизационно-статистического моделирования?