Структуры данных для предоставления графов
Потоки в транспортных сетях
Графы и сети. Определение.С формальной точки зрения граф представляет собой упорядоченную пару 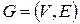 множеств, первое из которых состоит из вершин или узлов графа, а второе – из его рёбер или дуг.
множеств, первое из которых состоит из вершин или узлов графа, а второе – из его рёбер или дуг.
Ребро связывает между собой две вершины. При работе с графами часто возникает вопрос, как проложить путь из рёбер (или дуг) от одной вершины графа к другой? Поэтому в дальнейшем целесообразно говорить о движении по ребру. Это означает, что имеет место переход из вершины А графа в другую вершину В, связанную с ней ребром АВ. (При этом ребро графа, связывающее две вершины, для краткости обозначается парой этих вершин АВ, Рисунок 1).
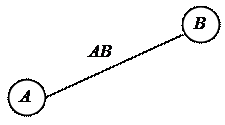
Рисунок 1 – Простейший граф: две вершины А и В, соединённые дугой АВ
Граф может быть ориентированным (орграфом) и не ориентированным. Рёбра не ориентированного графа, чаще всего называемого просто графом, можно проходить в обоих направлениях. В этом случае ребро графа – это неупорядоченная пара вершин или его концов.
В ориентированном графе, или орграфе, рёбра представляют собой упорядоченные пары вершин: первая вершина – это начало ребра; а вторая – его конец. Начало и конец ребра в ориентированном графе также могут совпадать.
Пример.
Автомагистраль или воздушная линия с двусторонним движением транспортных средств описывается не ориентированным графом или ориентированным графом с двумя дугами, имеющими разное указанное направление движения (Рисунок 2).

Рисунок 2 – Графовые модели двустороннего движения между вершинами А и В
Далее для краткости будем говорить о рёбрах, а ориентированы они или нет будет понятно из контекста.
Графически графы могут быть изображены двояко:
‑ вершины кружками с номером вершины, а ребра – отрезками прямых или кривых;
‑ вершины точками с указанием номера вершины рядом с точкой, а рёбра – отрезками прямых или кривых.
Далее дадим графическое изображение и аналитическое описание не ориентированного и ориентированного графов (Рисунки 3, 4).
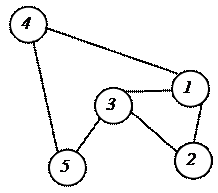
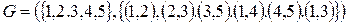
Рисунок 3 – Неориентированный граф и его аналитическое описание
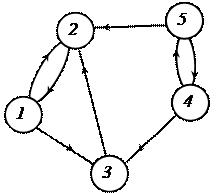
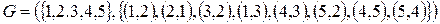
Рисунок 4 – Орграф и его аналитическое описание
Отметим особенности аналитического описания графов и орграфов.
При описании не ориентированного графа дуги описываются следующим образом: в круглых скобках указываются номера узлов, которые соединяет дуга; при этом первым указывается номер того узла, номер которого меньше.
При описании дуг ориентированного графа в круглых скобках на первом месте указывается номер пункта отправления, на втором – номер пункта назначения.
Определение.
Полный граф – это граф, в котором каждая вершина соединена со всеми остальными.
Число ребер в полном графе без петель с N вершинами равно 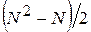 .
.
В полном ориентированном графе разрешается переход из любой вершины в любую другую.
Поскольку в графе переход по ребру разрешается в обоих направлениях, а переход по ребру в орграфе – только в одном, то в полном орграфе в два раза больше ребер, то есть их число равно 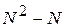 (Рисунок 5).
(Рисунок 5).
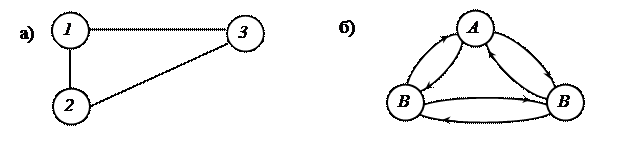
Рисунок 5 – а) Полный граф; N = 3; число рёбер равно 3;
б) Полный орграф; N = 3; число рёбер равно 6.
Определение.
Подграф 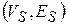 графа или орграфа
графа или орграфа 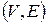 состоит из некоторого подмножества вершин
состоит из некоторого подмножества вершин 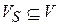 и некоторого подмножества ребер
и некоторого подмножества ребер 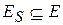 .
.
Определение.
Пусть в графе или орграфе ‑ это последовательность ребер, по которым можно поочередно проходить.
Другими словами, путь из вершины А в вершину В начинается в А и походит по набору ребер до тех пор, пока не будет достигнута вершина В.
С формальной точки зрения, путь из вершины 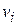 в вершину
в вершину 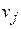 – это последовательность ребер графа
– это последовательность ребер графа 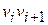 ,
, 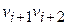 , …,
, …, 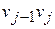 .
.
При этом требуется, чтобы любая вершина встречалась на таком пути не более чем один раз. У всякого пути есть длина – число ребер в нем (Рисунок 6).
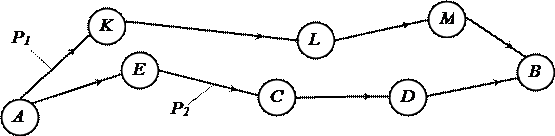
Рисунок 6 – Путь в графе. В данном случае имеет место два пути из вершины А в вершину В, определяемых суммой длин дуг:
для пути 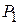 –
– 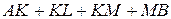 ;
;
для пути 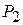 –
– 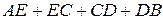 .
.
Определение.
Взвешенным графом или орграфом называется такой граф (или орграф), каждому ребру которого приписано число, называемое весом ребра.
При формальном описании вес ребра будет дополнительным элементом неупорядоченной или упорядоченной пары вершин. (образуя вместе с этой парой, так называемый, «триплет»)
Например, рассмотрим пару вершин С и D в ориентированном графе на рисунке 6. Припишем ребру СD некий вес 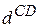 и в результате получим триплет
и в результате получим триплет
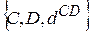 .
.
При проходе по ориентированному графу вес ребра считается ценой этого прохода.
Пример.
Стоимость перевозки по заданному сегменту (ребру) воздушной линии;
стоимость проезда по заданному отрезку платной автомагистрали и т.п.
В общем случае весом ребра в транспортных сетях может служить любой параметр, определяющий техническую оснащенность данного ребра сети: высота эшелона воздушной линии, ширина и число разрешенных полос движении на отрезке дорожной сети, пропускная способность трубопровода, разрешенная скорость движения и т.д.
Стоимость пути по взвешенному графу равна сумме весов всех ребер пути.
Определение.
Кратчайший путь во взвешенном графе – это путь с минимальным весом, даже если число ребер в пути можно и уменьшить (Рисунок 7).
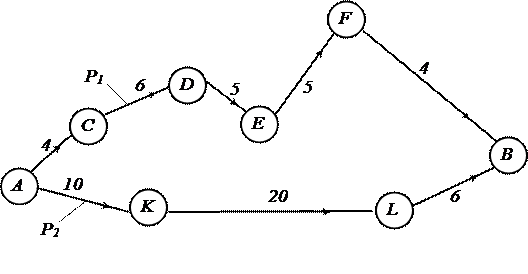
Рисунок 7 – Кратчайший путь во взвешенном графе: Р1=24усл.ед., Р2=36усл.ед.
Введем следующие обозначения для длины пути Р на графе.
Обозначим через 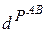 – длину пути из вершины А в вершину В.
– длину пути из вершины А в вершину В.
Тогда
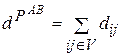 ,
,
где 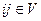 .
.
Длина кратчайшего пути на графе принимает обозначение
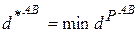
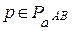 .
.
Здесь 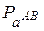 – множество альтернативных путей из А в В.
– множество альтернативных путей из А в В.
Далее введем определение сети.
Определение.
Граф или орграф, в котором вершины и ребра имеют некоторые количественные характеристики, называются сетью.
И, наконец, дадим определение связного графа и цикла на графе.
Определение.
Граф или орграф называется связным, если всякую пару узлов можно соединить, по крайней мере, одним путем.
Определение.
Цикл на графе – это путь, который начинается и кончается в одной и той же вершине (Рисунок 8).
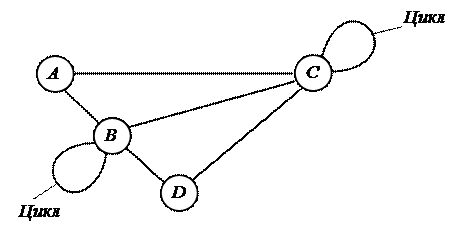
Рисунок 8 – Граф с циклами
В ациклическом графе или орграфе циклы отсутствуют.
Определение.
Связный ациклический граф называется деревом (Рисунок 9).
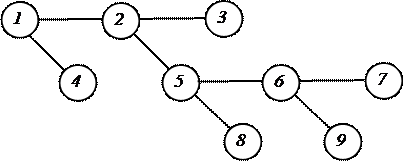
Рисунок 9 – Ациклический граф – дерево
Структуры данных для предоставления графов
Информацию о графах и орграфах можно хранить двумя способами:
1) в виде матрицы примыканий;
2) в виде списка примыканий.
Матрица примыканий обеспечивает быстрый доступ к информации о ребрах графа. Однако, если в графе мало ребер, то эта матрица будет содержать гораздо больше пустых клеток, чем заполненных.
Длина списки примыканий пропорциональна числу ребер в графе, однако, при пользовании списком, время получения информации о ребре увеличивается.
Таким образом, ни один из этих методов не превосходит другой заведомо.
Определение.
Матрица примыканий 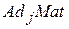 графа
графа 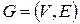 с числом вершин
с числом вершин 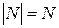 записывается в виде двумерного массива размера
записывается в виде двумерного массива размера 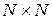 .
.
В каждой ячейке 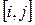 этого массива записано число «нуль» за исключением лишь тех случаев, когда из вершины
этого массива записано число «нуль» за исключением лишь тех случаев, когда из вершины 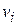 в вершину
в вершину 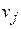 ведет ребро. Тогда в ячейке записывается «единица».
ведет ребро. Тогда в ячейке записывается «единица».
Более строго это можно записать так:
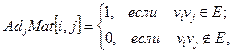
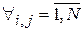 .
.
Рассмотрим, как будут выглядеть матрицы примыканий в конкретных примерах.
Пример.
Пусть задан граф следующего вида
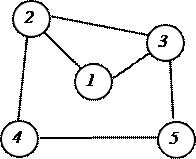
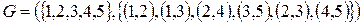 .
.
Матрица примыканий для этого графа принимает вид:
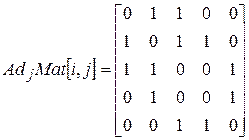 .
.
Матрица примыкания для неориентированного графа обладает следующими свойствами:
1) на главной диагонали расположены нулевые элементы;
2) матрица примыканий в данном случае является симметрической.
Пример.
Пусть задан орграф следующего вида
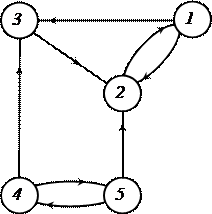
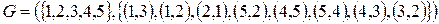 .
.
Матрица примыканий принимает вид:
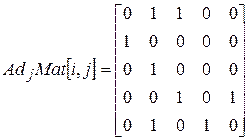 .
.
Матрица примыканий дл ориентированного графа обладает следующими свойствами:
1) на главной диагонали расположены нулевые элементы;
2) матрица примыканий является кососимметрической (антисимметрической).
Ячейка матрицы примыканий взвешенного графа или орграфа содержит 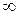 («бесконечность»), если соответствующее ребро отсутствует.
(«бесконечность»), если соответствующее ребро отсутствует.
Во всех остальных случаях ее значение равно весу ребра.
При этом диагональные элементы такой матрицы равны нулю, поскольку переход из вершины в нее саму не стоит ничего.
Рассмотрим пример.
В качестве примера возьмем дорожный граф из Октябрьского района г. Самары (Рисунок 10).
|

Рисунок 10 – Граф дорожной сети Октябрьского района г. Самары. Веса графа указаны в мерах
Для взвешенного графа рисунка 10 матрица примыканий приобретает вид (фрагмент):
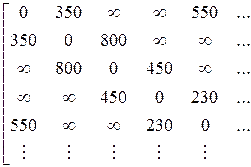 .
.
Полученная матрица является симметрической порядка 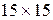 .
.
На главной диагонали находятся нули, означающие, что «стоимость перевозки» внутри самого узла теоретически равна нулю.
Предлагается студентам достроить эту матрицу до конца самостоятельно.
Определение.
Список примыканий 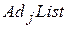 графа
графа 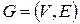 с числом вершин
с числом вершин 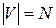 записывается в виде одномерного массива размера
записывается в виде одномерного массива размера 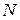 , каждый элемент которого представляет собой ссылку на список.
, каждый элемент которого представляет собой ссылку на список.
Рассмотрим построение списка примыканий для графа вида
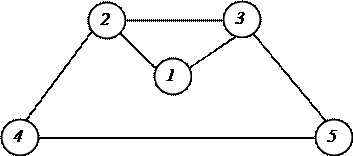
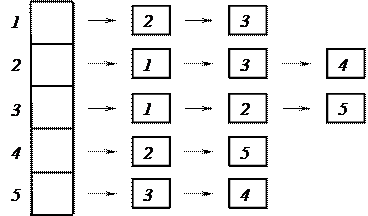
Список примыканий имеет следующий вид:
Дата добавления: 2022-07-20; просмотров: 109;










