Оценка погрешности интерполяционной формулы Лагранжа
Интерполяционный полином Лагранжа
Согласно условий (1), (2), предъявляемых к функции φ(х), запишем многочлен n-ой степени.
n
φ(х)≡Fn(x) = ∑ f(xi) pi(x) (6)
i=0
В узле xi многочлен (6) на основании (1) должен принимать значение fi. Значит, сомножитель pi(x) в точке xi должен быть равен 1,т.е.
pi (xi) = 1.
В то же время другие слагаемые многочлена (6) должны быть равны нулю, т.е.
pk (xi) = 0, i ≠ k, i, k = 0, 1, …,n.
Таким образом, мы сформулировали требования к сомножителю pi(x) , а именно:
pi (xi) = 1 , i = 0, 1, …,n (7)
pk (xi) = 0, i ≠ k; i, k = 0, 1, …,n. (8)
Сомножитель pi(x) называют вспомогательным многочленом степени n.
Учитывая свойство (8) и требование, чтобы многочлен pi(x) имел степень n, запишем:
pi(x) = ci (x-x0) (x-x1)… (x-xi-1) (x-xi+1) (x-xi+2)… (x-xn) (9)
где ci некоторый коэффициент.
При x = x0, x1,… xi-1, xi+1, … xn
pi(x) = 0.
Для определения ci обратимся к требованию (7). Из него следует:
pi(xi) = ci (xi-x0) (xi-x1)… (xi-xi-1) (xi-xi+1) (xi-xi+2)… (xi-xn) = 1
Тогда
ci= (10)
Сделав подстановку (10) в (9), получим окончательное выражение для pi(x):
pi(x) = (11)
Построенный многочлен (11), например, в точке x0 принимает значение p0(x0) = 1, а в остальных узлах – значения, равные нулю.
Многочлен p1(x) в точке x1 будет равен 1, а в остальных узлах обращается в 0, и т.д.
Таким образом, вспомогательный многочлен pi(x) полностью удовлетворяет требованиям (7), (8), а многочлен n-ой степени
n
Fn(x) = ∑ f(xi) pi(x)
i=0
является интерполяционным многочленом Лагранжа.
Замечание: многочлен Лагранжа целесообразнее использовать в задачах восстановления функции f(x) , когда точка интерполяции x расположена ближе к центру сетки.
Тестирование алгоритма
Рассмотрим функцию f(x), заданную таблицей:
| xi | ||||
| fi |
Построим многочлен Лагранжа для этой функции.
F3(x) = 2 + 1 + 2 +3
Если вместо x подставить 1, то Fn(1)= f1 = 2,
при x = 4 Fn(4)= f3 = 2 и т.д.
Следовательно, построенный многочлен удовлетворяет главному условию (1).
Таким образом, тестирование алгоритма будет состоять в следующем:
1. задать поочередно в качестве точек интерполяции табличные значения xi и получить соответствующие значения функции fi (при правильно работающей программе должно выполняться условие (1)).
2. задать в качестве точек интерполяции несколько значений, не являющихся узлами сетки, и проверить выполнение условия (2).
Оценка погрешности интерполяционной формулы Лагранжа
Пусть:
f(x) – Fn(x) = Rn(x),
тогда
f(x) = Fn(x) + Rn(x), (12)
Разность Rn(x) называется остаточным членом формулы Лагранжа. Значение Rn(x) равно погрешности, которая получается при замене значения функции f(x) значением интерполяционного многочлена Fn(x).
Если предположить, что функция f(x) имеет на отрезке [a, b]
(a = min {xk}; b = max {xk}) производные до порядка n+1,
k k
то для остаточного члена можно получить формулу
Rn(x) = f(n+1)(ξ) (13)
где точка ξ Î [a, b] и зависит от точки х.
Формулу (13) можно записать иначе:
Rn(x) =wn+1 (x). (14)
Если
max |f(n+1) (x)| £ Mn+1
x Î [a; b]
то получим оценку остаточного члена:
|Rn(x)| £ |wn+1 (x)|. (15)
Пример. Для функции у= 2х построим интерполяционный многочлен Лагранжа, выбрав узлами интерполирования точки
x0 = - 1, x1 = 0, x2 = 1, x3 = 2.
Вычислим соответствующие значения функции:
у0= ½ , у1=1, у2=2, у3=4;
по формуле Лагранжа найдем:
F3(x) =x3 + x2 +x+1.
Оценим погрешность, которая получается при замене функции у= 2х многочленом F3(x). Производная четвертого порядка
F(4)(x) = 2x(ln 2)4.
На отрезке [-1; 2] функция 2x возрастает, поэтому 0< 2x <= 4.
M4 = 4 (ln 2)4, ln 2 = 0,693…<, поэтому M4 < 4× = 1.
w4 (х) = x (x + 1)(x - 1)(x –2).
По формуле (15) получим:
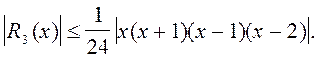
Многочлен Ньютона
Рассмотренный многочлен Лагранжа, как правило, используется в задачах восстановления функции f(x), когда точка интерполяции х находится ближе к центру сетки.
Если же точка интерполяции х расположена ближе к краям сетки, целесообразнее использовать многочлен Ньютона. Здесь возможны два случая:
1. точка интерполяции х находится вблизи первого узла сетки х0 (полином Ньютона I);
2. точка интерполяции х находится вблизи последнего узла сетки хn (полином Ньютона II).
Замечание. Построение многочлена Лагранжа основывается на вспомогательном многочлене pi(x).
В основе же построения многочлена Ньютона находится понятие конечной разности.
Определим понятие конечной разности.
Пусть функция задана таблицей с постоянным шагом h:
| хi | х0 | х1 | … | хi | … | хn |
| уi | у0 | у1 | … | уi | … | уn |
где хi = х0 + ih (i = 0, 1, …,n).
Тогда конечными или табличными разностями первого порядка или первыми разностями называются числа, равные приращениям значений функции
Dу0 =у1 – у0 = f(x1) – f(х0);
Dу1 =у2 – у1 = f(x2) – f(х1);
… … …
Dуn-1 =уn – уn-1 = f(xn) – f(хn-1).
Приращения разностей первого порядка называются разностями второго порядка:
D2у0 =Dу1 – Dу0 ,
D2у1 =Dу2 – Dу1.
Вообще разности любого порядка k определяются равенствами
Dkуm =Dk - 1уm +1 – Dk - 1уm.
Будем считать, что D0уm = уm.
Последовательно получаемые разности удобно записывать в форме таблицы:
| хi | уi | Dуi | D2уi | D3уi | … |
| х0 | у0 | ||||
| D у0 | |||||
| х1 | у1 | D2 у0 | |||
| Dу1 | D3 у0 | ||||
| х2 | у2 | D2 у1 | |||
| Dу2 | |||||
| х3 | у3 | ||||
| … | … |
Пример. Построим таблицу конечных разностей для функции
y = cosx на отрезке [0; 0,7] с шагом h = 0,1.
Таблица будет иметь вид:
| хi | уi 105 | Dуi 105 | D2уi105 | D3уi105 | D4уi105 | D5уi105 |
| 0,0 | 1,00000 | |||||
| -500 (D у0) | ||||||
| 0,1 | 0,99500 | -993 (D2 у0) | ||||
| -1493 (Dу1) | +13 (D3 у0) | |||||
| 0,2 | 0,98007 | -980 (D2 у1) | +12 | |||
| -2473 (Dу2) | 25 (D3 у1) | -2 | ||||
| 0,3 | 0,95534 | -950 (D2 у2) | +10 | |||
| -3428 (Dу3) | 35 (D3 у2) | -1 | ||||
| 0,4 | 0,92106 | -920 (D2 у3) | +9 | |||
| -4348 (Dу4) | 44 (D3 у3) | -3 | ||||
| 0,5 | 0,87758 | -876 (D2 у4) | +6 | |||
| -5224 (Dу5) | 50 (D3 у4) | |||||
| 0,6 | 0,82534 | -826 (D2 у5) | ||||
| -6050 (Dу6) | ||||||
| 0,7 | 0,76484 |
| <== предыдущая лекция | | | следующая лекция ==> |
| Погрешность решения. Исправление значений переменных. | | | Финансы предприятий (организаций) и задачи статистики |
Дата добавления: 2022-07-20; просмотров: 320;










